17.11: Canopy Flows
- Page ID
- 10599
17.11.1. Forests and Crops
The leaf or needle layer of a crop or forest is called a canopy. Individual plants or trees in these crops or forests each cause drag on the wind. The average winds in the air space between these plant-canopy or forest-canopy obstacles is the canopy flow.
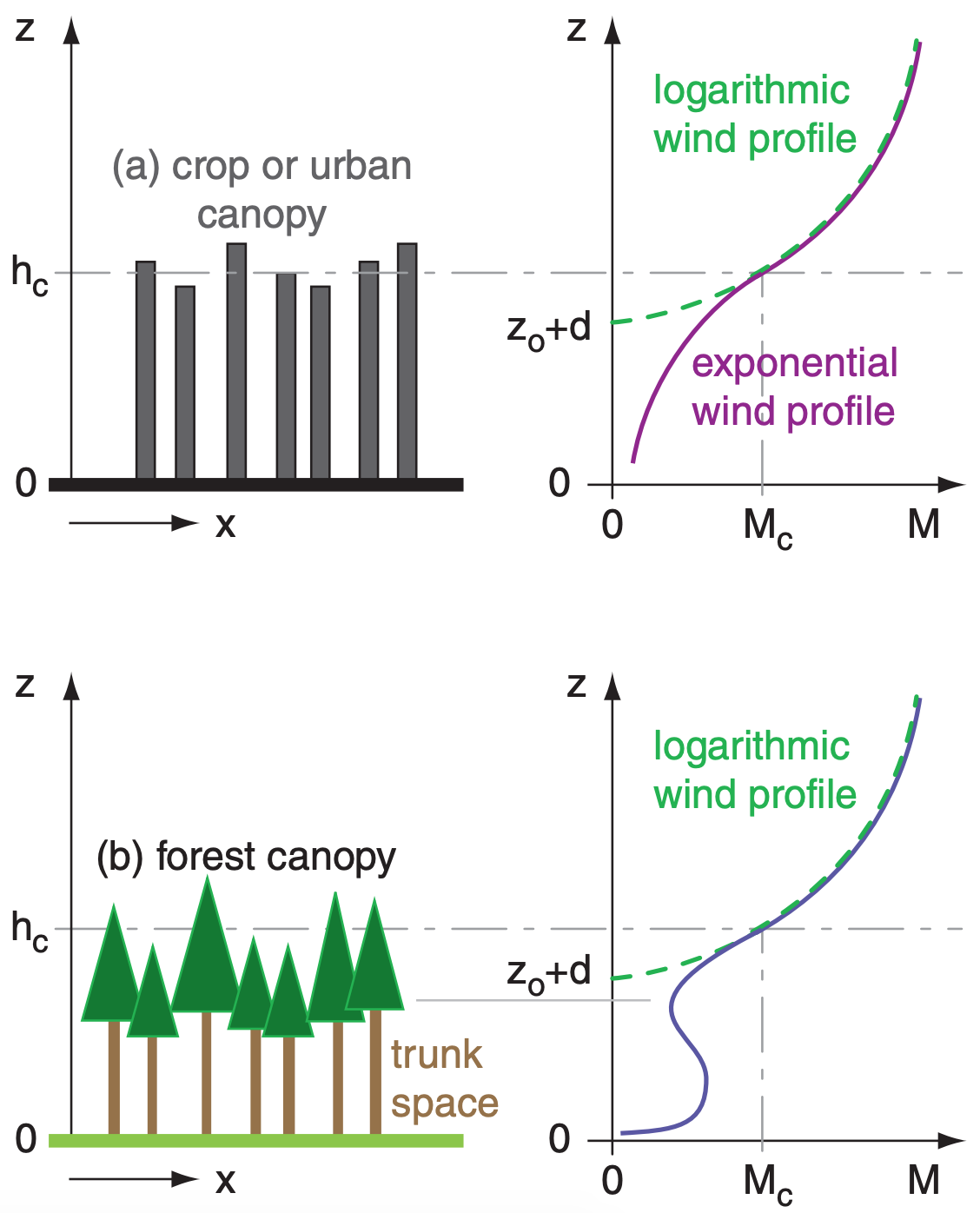
Just above the top of the canopy, the flow is approximately logarithmic with height (Fig. 17.40a). For statically neutral conditions in the surface layer:
\(\ \begin{align}
&M=\frac{u_{*}}{k} \ln \left(\frac{z-d}{z_{o}-d}\right)
&\text { for } z \geq h_{c}
\tag{17.53}\end{align}\)
where M is wind speed, z is height above ground, u* is the friction velocity (a measure of the drag force per unit surface area of the ground), k ≈ 0.4 is the von Kármán constant, d is the displacement distance (0 ≤ d ≤ hc), and zo is the roughness length, for an average canopy-top height of hc.
If you can measure the actual wind speed M at 3 or more heights z within 20 m above the top of the canopy, then you can use the following procedure to find d, zo, and u*: (1) use a spreadsheet to plot your M values on a linear horizontal axis vs. their [z–d] values on a logarithmic vertical axis; (2) experiment with different values of d until you find the one that aligns your wind points into a straight line; (3) extrapolate that straight line to M = 0, and note the resulting intercept on the vertical axis, which gives the roughness length zo. Finally, (4)pick any point exactly on the plotted line, and then plug in its M and z values, along with the d and zo values just found, to calculate u* using eq. (17.53).
If you do not have measurements of wind speed above the canopy top, you can use the following crude approximations to estimate the needed parameters: d ≈ 0.65·hc and zo ≈ 0.1·hc. Methods to estimate u* are given in the Boundary-Layer chapter.
The average wind speed at the average canopy-top height is Mc. For the crude approximations above, we find that Mc ≈ 3.13 u*.
Within the top 3/4 of canopy, an exponential formula describes the average wind-speed M profile:
\(\ \begin{align} M=M_{c} \cdot \exp \left[a \cdot\left(\frac{z}{h_{c}}-1\right)\right] \quad \text { for } 0.5 h_{c} \leq z \leq h_{c}\tag{17.54}\end{align}\)
where a is an attenuation coefficient that increases with increasing leaf area and decreases as the mean distance between individual plants increases. Typical values are: a ≈ 2.5 - 2.8 for oats and wheat; 2.0 - 2.7 for mature corn; 1.3 for sunflowers; 1.0 - 1.1 for larch and small evergreen trees; and 0.4 for a citrus orchard. The exponential and log-wind speeds match at the average canopy top hc.
For a forest with relatively open trunk space (i.e., only the tree trunks without many leaves, branches, or smaller underbrush), the previous equation fails. Instead, a weak relative maximum wind speed can occur (Fig. 17.40b). In such forests, if the canopy is very dense, then the sub-canopy (trunk space) flow can be relatively disconnected from the flow above the tree tops. Weak katabatic flows can exist in the trunk space day and night.
Sample Application (§)
Given these wind measurements over a 2 m high corn crop: [z (m), M (m s–1)] = [5, 3.87] , [10, 5.0] , [20, 6.01]. Find the displacement distance, roughness length, and friction velocity. If the attenuation coefficient is 2.5, plot wind speed M vs. height over 0.5 m ≤ z ≤ 5 m.
Find the Answer
Given: hc =2m, [z (m), M (m s–1)] listed above, a = 2.5.
Find: d = ? m, zo = ? m, u* = ? m s–1, and plot M vs. z.
Guess d = 0, and plot M vs. log(z–d) on a spreadsheet. This d is too small (see graph below), because the curve is concave up. Guess d = 4, which is too large, because curve is concave down. After other guesses (some not shown), I find that d = 1.3 m gives the straightest line.
Next, extrapolate on the semi-log graph to M = 0, which gives an intercept of zo = 0.2 m.
Solve eq. (17.53) for u* = k·M/ln[(z–d)/zo]
u* = 0.4(5m s–1)/ln[(10–1.3)/0.2] = 0.53 ms–1
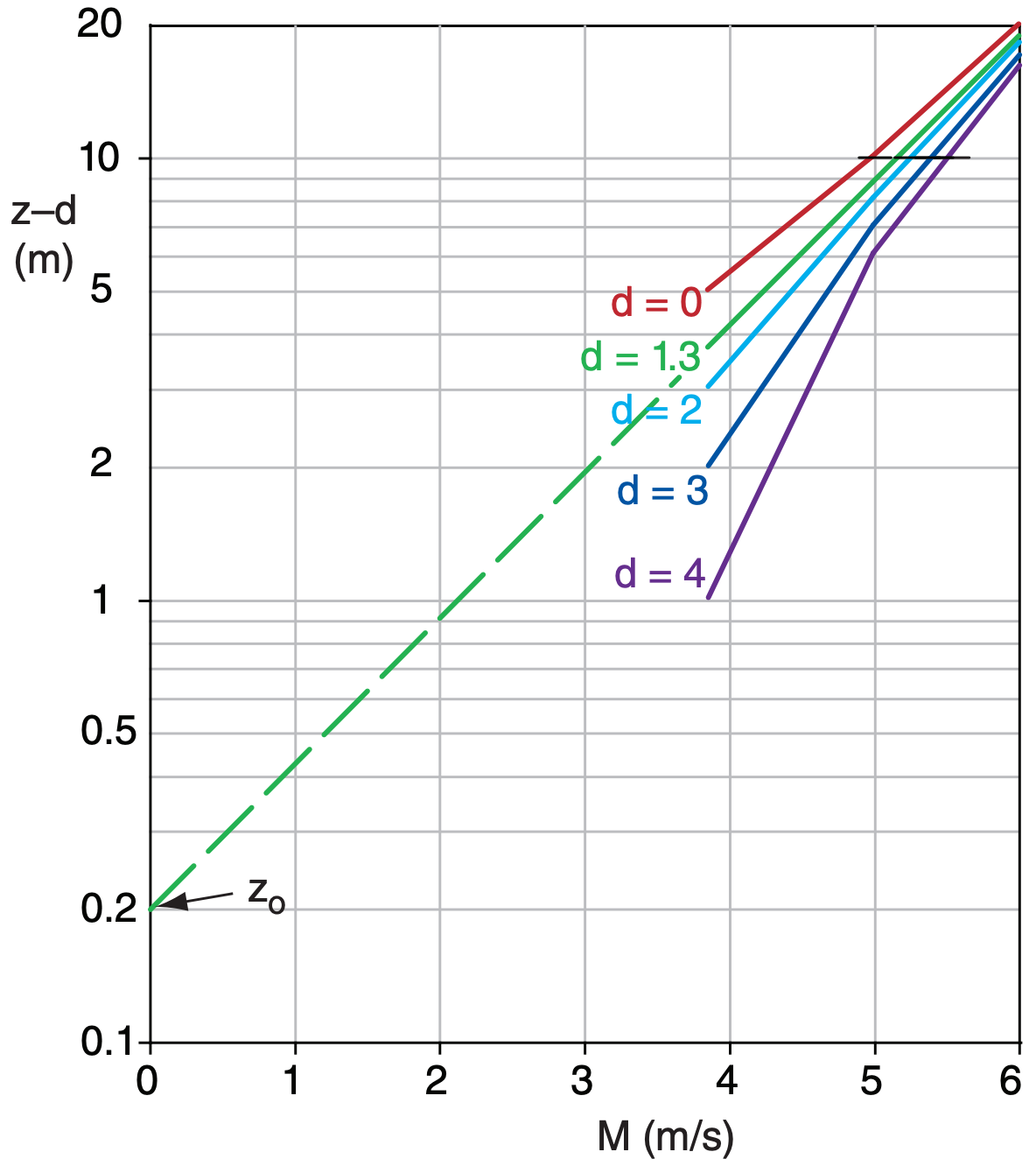
Solve eq. (17.53) for Mc at z = hc = 2 m:
Mc = [(0.53m s–1)/0.4] · ln[(2–1.3m)/0.2] = 1.66 m s–1
Use eq. (17.54) to find M for a range of heights below hc, and use eq. (17.53) for heights above hc:

Check: Shape of curve looks reasonable.
Exposition: For this exercise, zo = 0.1 hc, and d = 0.65 hc. Namely, the crude approximations are OK.
17.11.2. Cities
The collection of buildings and trees that make up a city is sometimes called an urban canopy. These obstacles cause an average canopy-flow wind similar to that for forests and crops (Fig. 17.40a).
However, winds at any one location in the city can be quite different. For example, the street corridors between tall buildings can channel flow similar to the flow in narrow valleys. Hence these corridors are sometimes called urban canyons. Also, taller buildings can deflect down to the surface some of the faster winds aloft. This causes much greater wind speeds and gusts near the base of tall buildings than near the base of shorter buildings.
Cities can be 2 - 12°C degrees warmer than the surrounding rural countryside — an effect called the urban heat island (UHI, Fig. 17.41). Reasons include the abundance of concrete, glass and asphalt, which capture and store the solar heat during daytime and reduce the IR cooling at night. Also, vegetated areas are reduced in cities, and rainwater is channeled away through storm drains. Hence, there is less evaporative cooling. Also, fuel and electrical consumption by city residents adds heat via heating, air conditioning, industry, and transportation.

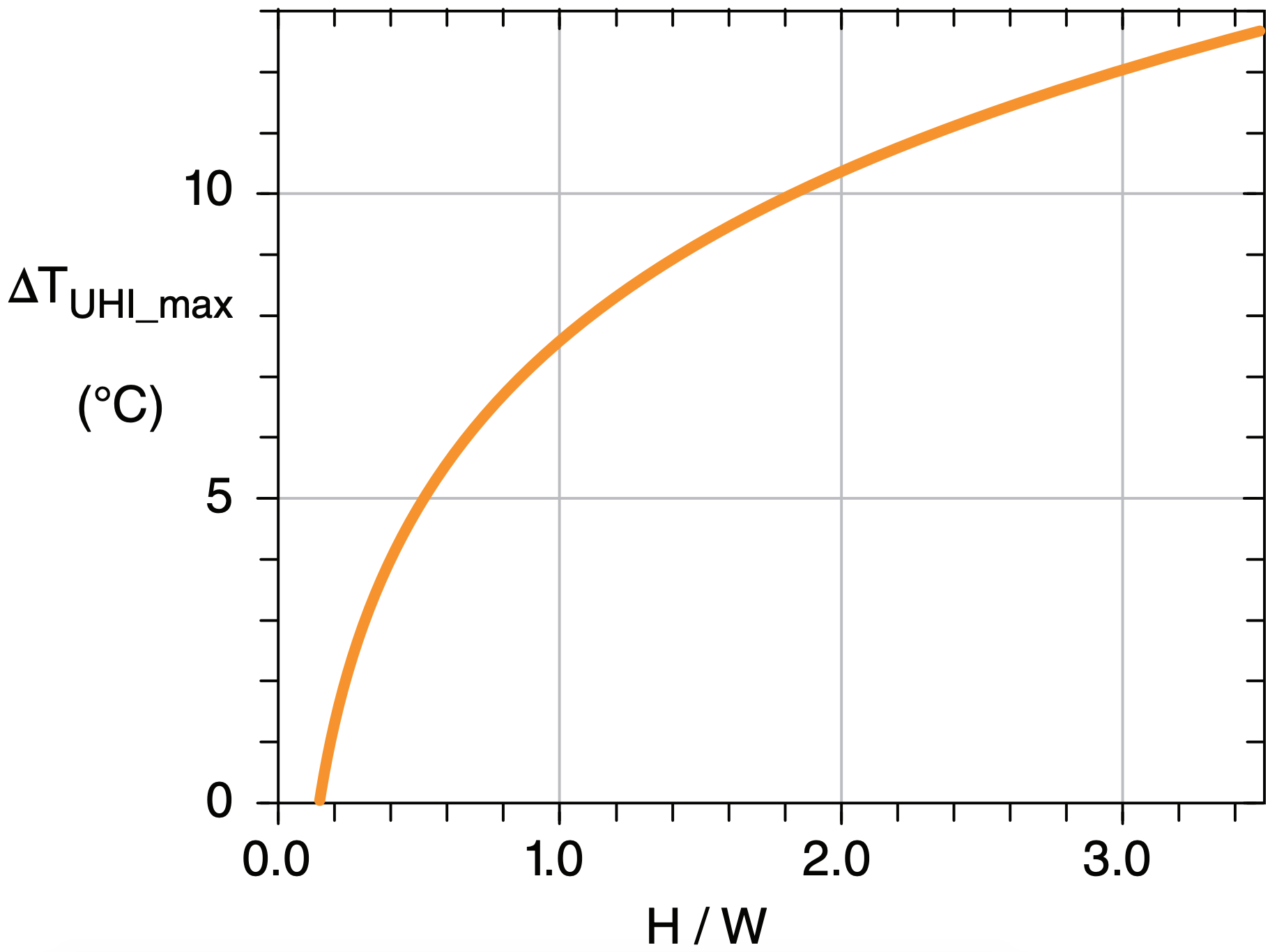
The city–rural temperature difference ∆TUHI is greatest during clear calm nights, because the city stays warm while rural areas cool considerably due to IR radiation to space. The largest values ∆TUHI_ max occur near the city center (Fig. 17.42), at the location of greatest density of high buildings and narrow streets. For clear, calm nights, this relationship is described by
\(\ \begin{align} \Delta T_{U H I_{-} \max} \approx a+b \cdot \ln (H / W)\tag{17.55}\end{align}\)
where a = 7.54°C and b = 3.97°C. H is the average height (m) of the buildings in the downtown city core, W is the average width (m) of the streets at the same location, and H/W is dimensionless.
Temperature difference is much smaller during daytime. When averaged over a year (including windy and cloudy periods of minimal UHI), the average ∆TUHI at the city center is only 1 to 2°C.
During periods of fair weather and light synopticscale winds, the warm city can generate circulations similar to sea breezes, with inflow of low-altitude rural air toward the city, and rising air over the hottest parts of town. These circulations can enhance clouds, and trigger or strengthen thunderstorms over and downwind of the city. With light to moderate winds, the UHI area is asymmetric, extending much further from the city in the downwind direction (Fig. 17.41), and the effluent (heat, air pollution, odors) from the city can be observed downwind as an urban plume (Fig. 17.43).


