17.1: Wind Frequency
- Page ID
- 9638
17.1.1. Wind-speed Frequency
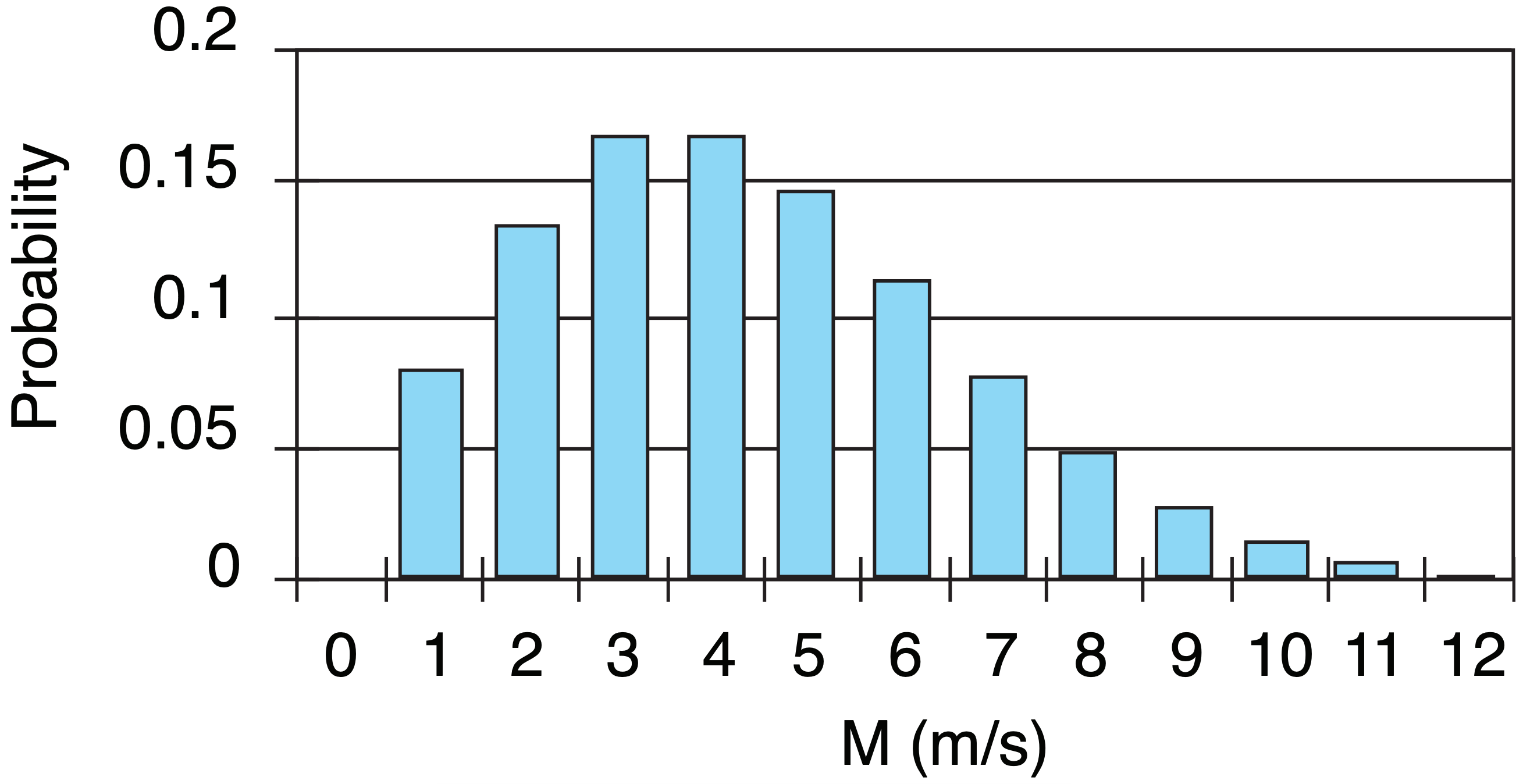
Wind speeds are rarely constant. At any one location, wind speeds might be strong only rarely during a year, moderate many hours, light even more hours, and calm less frequently (Fig. 17.1). The number of times that a range ∆M of wind speeds occurred in the past is the frequency of occurrence. Dividing the frequency by the total number of wind measurements gives a relative frequency. The expectation that this same relative frequency will occur in the future is the probability (Pr).
The probability distribution of mean wind speeds M at any location is described by the Weibull distribution:
\(\ \begin{align} \operatorname{Pr}=\frac{\alpha \cdot \Delta M \cdot M^{\alpha-1}}{M_{o}^{\alpha}} \cdot \exp \left[-\left(\frac{M}{M_{o}}\right)^{\alpha}\right]\tag{17.1}\end{align}\)
where Pr is the probability (or relative frequency) of wind speed M± 0.5·∆M. Such wind-speed variations are caused by synoptic, mesoscale, local and boundary-layer processes.
Location parameter Mo is proportional to the mean wind speed. For spread parameter α, smaller α causes wider spread of winds about the mean. Values of the parameters and the corresponding distribution shape vary from place to place.
The bin size or resolution is ∆M. For example, the column plotted in Fig. 17.1 for M = 3 m s–1 is the probability that the wind is between 2.5 and 3.5 m s–1. The width of each column in the histogram is ∆M = 1 m s–1. The sum of probabilities for all wind speeds should equal 1, meaning there is a 100% chance that the wind speed is between zero and infinity. Use this to check for errors. Eq. (17.1) is only approximate, so the sum of probabilities almost equals 1.
Wind-speed distributions are useful to estimate electrical power generation by wind turbines, and when designing buildings and bridges to withstand extreme winds.
You can express extreme-wind likelihood as a return period (RP), which is equal to the total period of measurement divided by the number of times the wind exceeded a threshold. For example, if winds exceeding 30 m s–1 occurred twice during the last century, then the return period for 30 m s–1 winds is RP = (100 yr)/2 = 50 years. Faster winds occur less frequently, and have greater return periods.
17.1.2. Wind-direction Frequency
By counting the frequency of occurrence that winds came from each compass direction (N, NNE, NE, etc.) over a period such as 10 years, and then plotting that frequency on a polar graph, the result is called a wind rose. For example, Fig. 17.2 shows the wind rose for Vancouver Airport (CYVR).
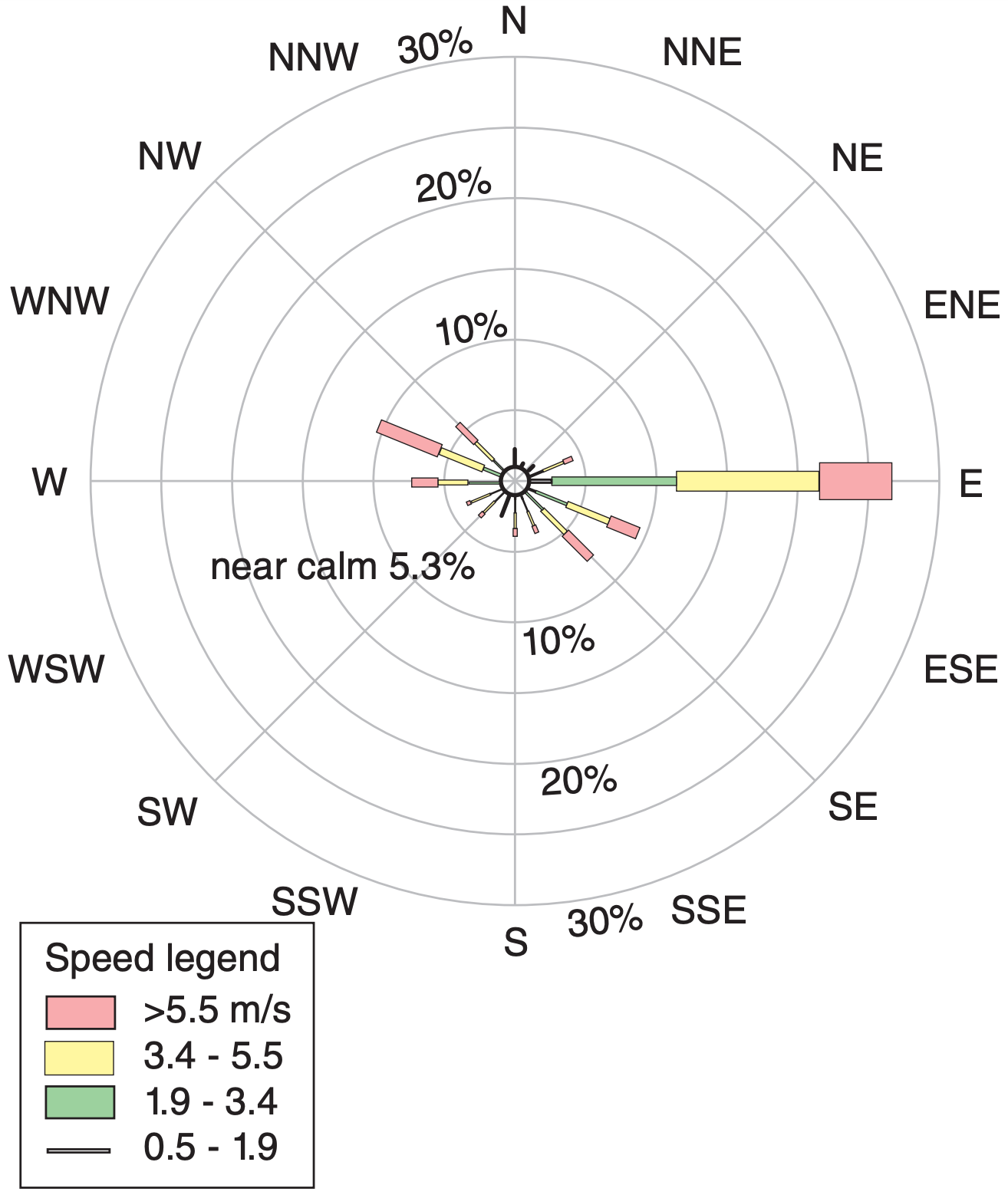
The total length of each wind line gives the total frequency of any wind speed from that direction, while the width (or color) of the line subdivides that frequency into the portions associated with various wind speeds. (Not all wind roses are subdivided by wind speed.) The frequency of calm winds is usually written in the center of the circle if it fits, or is indicated off to the side. The sum of all the frequencies (including calm) should total 100%. At a glance, the longest lines indicate the predominant wind directions for any location.
For example, at Vancouver Airport, East (E) winds (winds from the east) are most frequent, followed by winds from the WNW and then from the ESE. Aircraft take-offs and landings are safer — and require shorter distances — if they are done into the wind. Hence, airports are built with their runways aligned parallel to the predominant wind directions (within reason, as dictated by property boundaries and obstacles).
Sample Application
How frequent are east winds at Vancouver airport?
Find the Answer
Use Fig. 17.2. Frequency ≈ 26% .
Exposition: This is the sum of 2% for 0.5 < M ≤ 1.9, plus 9% for 1.9 < M ≤ 3.4, plus 10% for 3.4 < M ≤ 5.5, plus 5% for M > 5.5 m s–1.
Fig. 17.3 shows that the runways at Vancouver Airport are appropriate for the wind climatology of the previous figure. The end of each runway is labeled with the magnetic compass direction (in tens of degrees; e.g., 12 means 120° magnetic) towards which the aircraft is flying when approaching that end of the runway from outside the airport. Thus, aircraft will use runway 30 for winds from 300°. Parallel runways are labeled as left (L) or right (R).