6.1: Processes Causing Saturation
- Page ID
- 9561
Clouds are saturated portions of the atmosphere where small water droplets or ice crystals have fall velocities so slow that they appear visibly suspended in the air. Thus, to understand clouds we need to understand how air can become saturated.
6.1.1 Cooling and Moisturizing
Unsaturated air parcels can reach saturation by three processes: cooling, adding moisture, or mixing. The first two processes are shown in Figure 6.1, where saturation is reached by either cooling until the temperature equals the dew point temperature, or adding moisture until the dew point temperature is raised to the actual ambient temperature.
The temperature change necessary to saturate an air parcel by cooling it is:
\[\begin{align} \Delta T=T_{d}-T \label{6.1} \end{align}\]
Whether this condition is met can be determined by finding the actual temperature change based on the first law of thermodynamics (see Chapter 3).

The moisture addition necessary to reach saturation is
\[\begin{align} \Delta r=r_{S}-r \label{6.2}\end{align}\]
Whether this condition is met can be determined by using the moisture budget to find the actual humidity change (see the Water Vapor chapter).
In the real atmosphere, sometimes both cooling and moisturizing happen simultaneously. Schematically, this would correspond to an arrow from parcel A diagonally to the saturation line of Figure 6.1.
Clouds usually form by adiabatic cooling of rising air. Air can be rising due to its own buoyancy (making cumuliform clouds), or can be forced up over hills or frontal boundaries (making stratiform clouds). Once formed, infrared radiation from cloud top can cause additional cooling to help maintain the cloud.
Sample Application
Air at sea level has a temperature of 20°C and a mixing ratio of 5 g kg–1. How much cooling OR moisturizing is necessary to reach saturation?
Find the Answer
Given: T = 20°C, r = 5 g kg–1
Find: ∆T = ? °C, ∆r = ? g kg–1.
Use Table 4-1 because it applies for sea level. Otherwise, solve equations or use a thermo diagram.
At T = 20°C, the table gives rs = 14.91 g kg–1.
At r = 5 g kg–1, the table gives Td = 4 °C .
Use Equation \ref{6.1}: ∆T = 4 – 20 = –16°C needed.
Use Equation \ref{6.2}: ∆r = 14.91 – 5 = 9.9 g kg–1 needed.
Check: Units OK. Physics OK.
Exposition: This air parcel is fairly dry. Much cooling or moisturizing is needed.
6.1.2. Mixing
Mixing of two unsaturated parcels can result in a saturated mixture, as shown in Figure 6.2. Jet contrails and your breath on a cold winter day are examples of clouds that form by the mixing process.
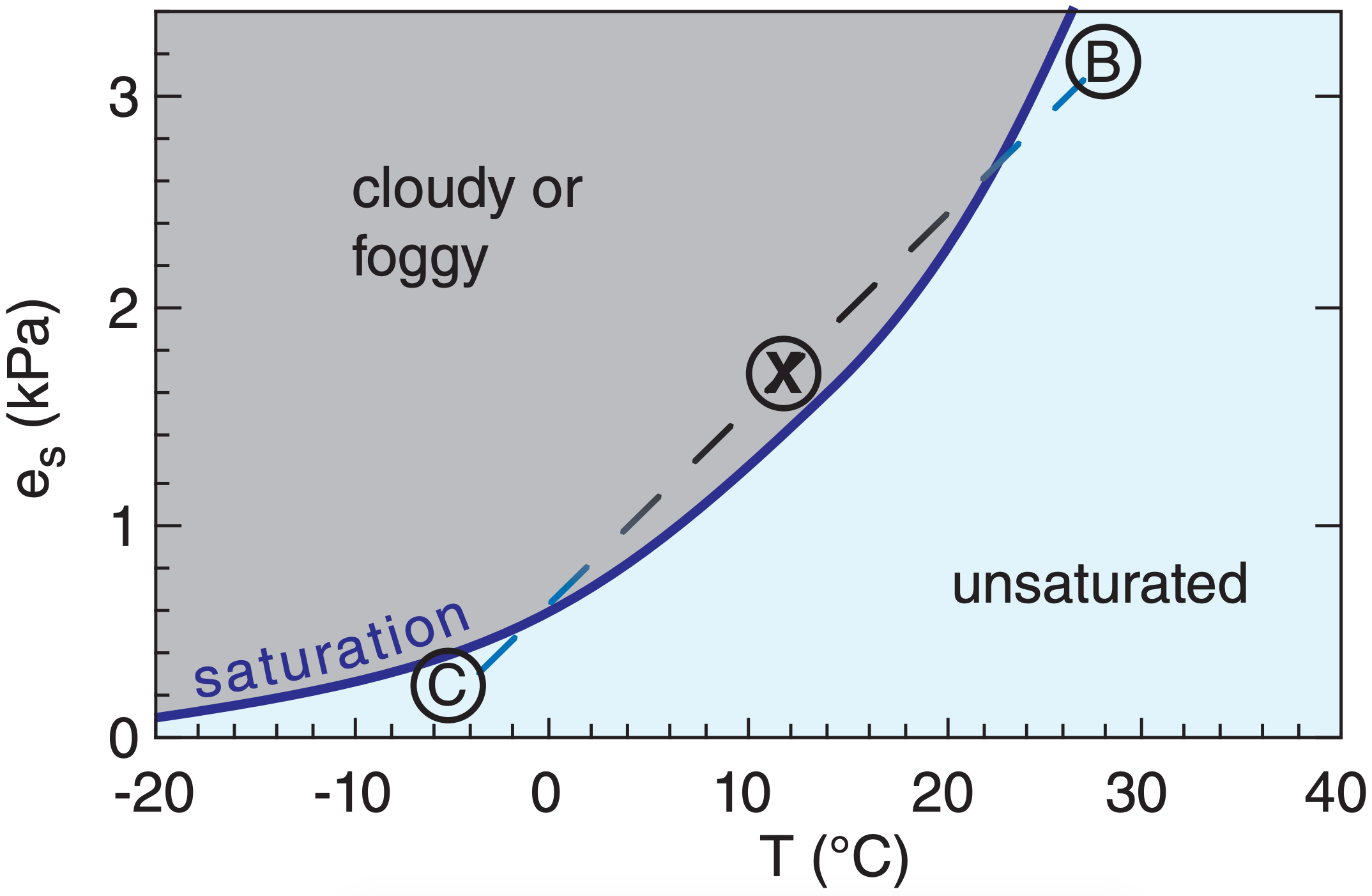
Mixing essentially occurs along a straight line in this graph connecting the thermodynamic states of the two original air parcels. However, the saturation line (given by the Clausius-Clapeyron equation) is curved, so a mixture can be saturated even if the original parcels are not.
Let mB and mC be the original masses of air in parcels B and C, respectively. The mass of the mixture (parcel X) is :
\(\ \begin{align} m_{X}=m_{B}+m_{C}\label{6.3}\end{align}\)
The temperature and vapor pressure of the mixture are the weighted averages of the corresponding values in the original parcels:
\(\ \begin{align} T_{X}=\frac{m_{B} \cdot T_{B}+m_{C} \cdot T_{C}}{m_{X}}\label{6.4}\end{align}\)
\(\ \begin{align}e_{X}=\frac{m_{B} \cdot e_{B}+m_{C} \cdot e_{C}}{m_{X}}\label{6.5}\end{align}\)
Specific humidity or mixing ratio can be used in place of vapor pressure in eq. (6.5).
Instead of using the actual masses of the air parcels in eqs. (6.3) to (6.5), you can use the relative portions that mix. For example, if the mixture consists of 3 parts B and 2 parts C, then you can use mB = 3 and mC = 2 in the equations above.
Sample Application
Suppose that the state of parcel B is T = 30°C with e = 3.4 kPa, while parcel C is T = –4°C with e = 0.2 kPa. Both parcels are at P = 100 kPa. If each parcel contains 1 kg of air, then what is the state of the mixture? Will the mixture be saturated?
Find the Answer
Given: B has T = 30°C, e = 3.4 kPa, P = 100 kPa
C has T = –4°C, e = 0.2 kPa, P = 100 kPa
Find: T = ? °C and e = ? kPa for mixture (at X).
Use eq. (6.3): mX = 1 + 1 = 2 kg
Use eq. (6.4): TX = [(1kg)·(30°C) + (1kg)·(–4°C)]/(2kg) = 13°C
Use eq. (6.5): eX = [(1kg)·(3.4 kPa) + (1kg)·(0.2 kPa)]/(2kg) = 1.8 kPa
P hasn’t changed. P = 100 kPa.
Check: Units OK. Physics OK.
Exposition: At T = 13°C, Table 4-1 gives es = 1.5 kPa. Thus, the mixture is saturated because its vapor pressure exceeds the saturation vapor pressure. This mixture would be cloudy/foggy


