3.0: Homework Exercises
- Page ID
- 9873
3.10.1. Broaden Knowledge & Comprehension
B1(§). For an upper-air weather station near you (or for a site specified by your instructor), get recent observation data of T vs. z or T vs. P from the internet, and plot the result on a copy of the thermodynamic diagram from this chapter.
B2. For an upper-air weather station near you (or for a site specified by your instructor), get an already-plotted recent sounding from the internet. Find the background isotherm and isobar lines, and compare their arrangement to the diagram (Figure 3.4) in this chapter. We will learn more about other thermo-diagram formats in the Atmospheric Stability chapter.
B3. Use the internet to acquire temperatures at your town and also at a town about 100 km downwind of you. Also get the wind speeds in both towns and take an average. Use this average speed to calculate the contribution of advection to the local heating in the air between those two towns.
B4. Use the internet to acquire a weather map or other weather report that shows the observed nearsurface air temperature just before sunrise at your location (or at another location specified by your instructor). For the same location, find a map or report of the temperature in mid afternoon. From these two observations, calculate the rate of temperature change over that time period. Also, qualitatively describe which terms in the Eulerian heat budget might be largest. (Hint: if windy, then perhaps advection is important. If clear skies, then heat transfer from the solar-heated ground might be important. Access other weather maps as needed to determine which physical process is most important for the temperature change.)
B5. Use the internet to acquire a local weather map of apparent temperature, such as wind-chill in winter or heat index (or humidex) in summer. If the map covers your location, compare how the air feels to you vs. the apparent temperature on the map.
B6. Use the internet to acquire images of 4 different types of temperature sensors (not 4 models of the same type of sensor).
3.10.2. Apply
A1. Find the change in sensible heat (enthalpy) (J) possessed by 3 kg of air that warms by __°C.
| a. 1 | b. 2 | c. 3 | d. 4 | e. 5 | f. 6 |
| g. 7 | h. 8 | i. 9 | j. 10 | k. 11 | m. 12 |
A2. Find the specific heat Cp of humid air having water-vapor mixing ratio (gvapor/gdry air) of:
| a. 0.010 | b. 0.012 | c. 0.014 | d. 0.016 | e. 0.018 | f. 0.020 |
| h. 0.022 | i. 0.024 | j. 0.026 | k. 0.028 | m. 0.030 |
A3. Find the change in latent heat (J) for condensation of ___ kg of water vapor.
| a. 0.2 | b. 0.4 | c. 0.6 | d. 0.8 | e. 1.0 | f. 1.2 |
| g. 1.4 | h. 1.6 | i. 1.8 | j. 2.0 | k. 2.2 | m. 2.4 |
A4. Find the temperature change (°C) of air given the following values of heat transfer and pressure change, assuming air density of 1.2 kg m–3.
| ∆q (J kg–1) | ∆P (kPa) | |
| a. | 500 | 5 |
| b. | 1000 | 5 |
| c. | 1500 | 5 |
| d. | 2000 | 5 |
| e. | 2500 | 5 |
| f. | 3000 | 5 |
| g. | 500 | 10 |
| h. | 1000 | 10 |
| i. | 1500 | 10 |
| j. | 2000 | 10 |
| k. | 2500 | 10 |
| m. | 3000 | 10 |
A5. Find the change in temperature (°C) if an air parcel rises the following distances while experiencing the heat transfer values given below.
| ∆q (J kg–1) | ∆z (km | |
| a. | 500 | 0.5 |
| b. | 1000 | 0.5 |
| c. | 1500 | 0.5 |
| d. | 2000 | 0.5 |
| e. | 2500 | 0.5 |
| f. | 3000 | 0.5 |
| g. | 500 | 1 |
| h. | 1000 | 1 |
| i. | 1500 | 1 |
| j. | 2000 | 1 |
| k. | 2500 | 1 |
| m. | 3000 | 1 |
A6. Given the following temperature change ∆T (°C) across a height difference of ∆z = 4 km, find the lapse rate (°C km–1):
| a. 2 | b. 5 | c. 10 | d. 20 | e. 30 | f. 40 |
| g. 50 | h. –2 | i. –5 | j. –10 | k. –20 | m. –30 |
A7. Find the final temperature (°C) of an air parcel with the following initial temperature and height change, for an adiabatic process.
| Tinitial (°C) | ∆z (km) | |
| a. | 15 | 0.5 |
| b. | 15 | –1.0 |
| c. | 15 | 1.5 |
| d. | 15 | –2.0 |
| e. | 15 | 2.5 |
| f. | 15 | –3.0 |
| g. | 5 | 0.5 |
| h. | 5 | –1.0 |
| i. | 5 | 1.5 |
| j. | 5 | –2.0 |
| k. | 5 | 2.5 |
| m. | 5 | –3.0 |
A8. Using the equations (not using the thermo diagram), find the final temperature (°C) of dry air at a final pressure, if it starts with the initial temperature and pressure as given. (Assume adiabatic.)
| Tinitial (°C) | Pinitial (kPa) | Pfinal(kPa) | |
| a. | 5 | 100 | 80 |
| b. | 5 | 100 | 50 |
| c. | 5 | 80 | 50 |
| d. | 5 | 80 | 100 |
| e. | 0 | 60 | 80 |
| f. | 0 | 60 | 50 |
| g. | 0 | 80 | 40 |
| h. | 0 | 80 | 100 |
| i. | –15 | 90 | 80 |
| j. | –15 | 90 | 50 |
| k. | –15 | 70 | 50 |
| m. | –15 | 70 | 100 |
A9. Same as previous question, but use the thermo diagram Figure 3.4.
A10. Given air with temperature and altitude as listed below, use formulas (not thermo diagrams) to calculate the potential temperature. Show all steps in your calculations.
| z (m) | T (°C) | |
| a. | 400 | 30 |
| b. | 800 | 20 |
| c. | 1,100 | 10 |
| d. | 1,500 | 5 |
| e. | 2,000 | 0 |
| f | 6,000 | –50 |
| g. | 10,000 | –90 |
| h. | –30 | 35 |
| i. | 700 | 3 |
| j. | 1,300 | –5 |
| k. | 400 | 5 |
| m. | 2,000 | –20 |
A11. Same as the previous exercise, but find the virtual potential temperature for humid air. Use a water-vapor mixing ratio of 0.01 gvapor/gdry air if the air temperature is above freezing, and use 0.0015 gvapor/gdry air if air temperature is below freezing. Assume the air contains no ice or liquid water.
A12. Given air with temperature and pressure as listed below, use formulas (not thermo diagrams) to calculate the potential temperature. Show all steps in your calculations.
| P (kPa) | T (°C) | |
| a. | 90 | 30 |
| b. | 80 | 20 |
| c. | 110 | 10 |
| d. | 70 | 5 |
| e. | 85 | 0 |
| f. | 40 | –45 |
| g. | 20 | –90 |
| h. | 105 | 35 |
| i. | 75 | 3 |
| j. | 60 | –5 |
| k. | 65 | 5 |
| m. | 50 | –20 |
A13. Same as previous exercise, but use the thermo diagram Figure 3.4.
A14. Instead of equations, use the Fig 3.4 to find the actual air temperature (°C) given:
| P(kPa) | θ (°C) | |
| a. | 100 | 30 |
| b. | 80 | 30 |
| c. | 60 | 30 |
| d. | 90 | 10 |
| e. | 70 | 10 |
| f. | 50 | 10 |
| g. | 80 | –10 |
| h. | 50 | –10 |
| i. | 20 | 50 |
A15(§). Use a spreadsheet to calculate and plot a thermo diagram similar to Figure 3.4 but with: isotherm grid lines every 10°C, and dry adiabats for every 10°C from –50°C to 80°C.
A16. Find the rate of temperature change (°C h–1) in an Eulerian coordinate system with no internal heat source, given the kinematic flux divergence values below. Assume ∆x = ∆y = ∆z = 1 km.
| ∆Fx (K·m s–1) | ∆Fy (K·m s–1) | ∆Fz (K·m s–1) | |
| a. | 1 | 2 | 3 |
| b. | 1 | 2 | –3 |
| c. | 1 | –2 | 3 |
| d. | 1 | –2 | –3 |
| e. | –1 | 2 | 3 |
| f. | –1 | 2 | –3 |
| g. | –1 | –2 | 3 |
| h. | –1 | –2 | –3 |
A17. Given the wind and temperature gradient, find the value of the kinematic advective flux gradient (°C h–1).
| V (m s–1) | ∆T/∆y (°C 100 km) | |
| a. | 5 | –2 |
| b. | 5 | 2 |
| c. | 10 | –5 |
| d. | 10 | 5 |
| e. | –5 | –2 |
| f. | –5 | 2 |
| g. | –10 | –5 |
| h. | –10 | 5 |
A18. Given the wind and temperature gradient, find the value of the kinematic advective flux gradient (°C h–1).
| W (m s–1) | ∆T/∆z (°C km–1) | |
| a. | 5 | –2 |
| b. | 5 | 2 |
| c. | 10 | –5 |
| d. | 10 | –10 |
| e. | –5 | –2 |
| f. | –5 | 2 |
| g. | –10 | –5 |
| h. | –10 | –10 |
A19. Find the value of the conductive flux Fz cond (W m–2) given a change of absolute temperature with height (T2 – T1 = value below) across a distance (z2 – z1 = 1 m):
| a. –1 | b. –2 | c. –3 | d. –4 | e. –5 | f. –6 | g. –7 |
| h. 1 | i. 2 | j. 3 | k. 4 | m. 5 | n. 6 | o. 7 |
A20. Find the effective surface turbulent heat flux (°C·m s–1) over a forest for wind speed of 10 m s–1, air temperature of 20°C, and surface temperature (°C) of
| a. 21 | b. 22 | c. 23 | d. 24 | e. 25 | f. 26 | g. 27 |
| h. 19 | i. 18 | j. 17 | k. 16 | m. 15 | n. 14 | o. 13 |
A21. Find the effective kinematic heat flux at the surface on a calm day, for a buoyant velocity scale of 50 m s–1, a mixed-layer potential temperature of 25°C, and with a surface potential temperature (°C) of:
| a. 26 | b. 28 | c. 30 | d. 32 | e. 34 | f. 36 | g. 38 |
| h. 40 | i. 42 | j. 44 | k. 46 | m. 48 | n. 50 |
A22. Find the effective kinematic heat flux at the surface on a calm day, for a Deardorff velocity of 2ms–1, a mixed-layer potential temperature of 24°C, and with a surface potential temperature (°C) of:
| a. 26 | b. 28 | c. 30 | d. 32 | e. 34 | f. 36 | g. 38 |
| h. 40 | i. 42 | j. 44 | k. 46 | m. 48 | n. 50 |
A23. For dry air, find the buoyancy velocity scale, given a mixed-layer potential temperature of 25°C, a mixed-layer depth of 1.5 km, and with a surface potential temperature (°C) of:
| a. 27 | b. 30 | c. 33 | d. 36 |
| e. 40 | f. 43 | g. 46 | h. 50 |
A24. For dry air, find the Deardorff velocity w* for an effective kinematic heat flux at the surface of 0.2 K·m s–1, air temperature of 30°C, and mixed-layer depth (km) of:
| a. 0.4 | b. 0.6 | c. 0.8 | d. 1.0 |
| e. 1.2 | f. 1.4 | g. 1.6 | h. 1.8 |
A25. Find the value of vertical divergence of kinematic heat flux, if the flux at the top of a 200 m thick air layer is 0.10 K·m s–1, and flux ( K·m s–1) at the bottom is:
| a. 0.2 | b. 0.18 | c. 0.16 | d. 0.14 |
| e. 0.12 | f. 0.10 | g. 0.08 | h. 0.06 |
A26. Given values of effective surface heat flux and boundary-layer depth for daytime during fair weather, what is the value of the turbulent-flux vertical gradient?
| FH (K·m·s–1) | zi (km) | |
| a. | 0.25 | 2.0 |
| b. | 0.15 | 1.5 |
| c. | 0.1 | 1.0 |
| d. | 0.03 | 0.3 |
| e. | 0.08 | 0.3 |
| f. | 0.12 | 0.8 |
| g. | 0.15 | 1.0 |
| h. | 0.25 | 1.5 |
A27. Given a pre-storm environment where the temperature varies linearly from 25°C at the Earth’s surface to –60°C at 11 km (tropopause). What is the value of the vertical gradient of turbulent flux (K s–1) for an altitude (km) of:
| a. 0.1 | b. 0.5 | c. 1 | d. 1.5 | e. 2 | f. 2.5 | g. 3 |
| h. 3.5 | i. 4 | j. 5 | k. 6 | m. 7 | n. 8 | o. 11 |
A28. Find the mid-tropospheric maximum value of heat flux (K·m s–1) for a stormy atmosphere, where the troposphere is 11 km thick, and the air temperature at the top of the troposphere equals the air temperature of a standard atmosphere. But the air temperature (°C) at the ground is:
| a. 16 | b. 17 | c. 18 | d. 19 | e. 20 | f. 21 | g. 22 |
| h. 23 | i. 24 | j. 25 | k. 26 | m. 27 | n. 28 | o. 29 |
A29. Find the latent-heating rate (°C h–1) averaged over the troposphere for a thunderstorm when the rainfall rate (mm h–1) is:
| a. 0.5 | b. 1 | c. 1.5 | d. 2 | e. 2.5 | f. 3 | g. 3.5 |
| h. 4 | i. 4.5 | j. 5 | k. 5.5 | m. 6 | n. 6.5 | o. 7 |
A30. Given below the net radiative flux (W m–2) reaching the surface, find the sum of sensible and latent heat fluxes (W m–2) at the surface. (Hint: determine if it is day or night by the sign of the radiative flux.)
| a. –600 | b. –550 | c. –500 | d. –450 | e. –400 |
| f. –350 | g. –300 | h. –250 | i. –200 | j. –150 |
| k. –100 | m. –50 | n. 50 | o. 100 | p. 150 |
A31. Same as the previous problem, but estimate the values of the sensible and latent heat fluxes (W m–2) assuming a Bowen ratio of:
| (1) 0.2 | (2) 5.0 |
A32. Suppose you mounted instruments on a tower to observe temperature T and mixing ratio r at two heights in the surface layer (bottom 25 m of atmosphere) as given below. If a net radiation of –500 W m–2 was also measured at that site, then estimate the values of effective surface values of sensible heat flux and latent heat flux.
| index | z(m) | T(°C) | r (gvap/kgair |
| 2 | 10 | T2 | 10 |
| 1 | 2 | 20 | 15 |
where T2 (°C) is:
| a. 13.5 | b. 13 | c. 12.5 | d. 12 | e. 11.5 | f. 11 |
| g. 10.5 | h. 10 | i. 9.5 | j. 9 | k. 8.5 | m. 8 |
A33. Not only can a stationary person feel wind chill when the wind blows, but a moving person in a calm wind can also feel wind chill, because most important is the speed of the air relative to the speed of the body. If you move at the speed given below through calm air of temperature given below, then you would feel a wind chill of what apparent temperature? Given: M (m s–1), T (°C) .
| a. 5, 5 | b. 10, 5 | c. 15, 5 | d. 20, 5 | e. 25, 5 |
| f. 30, –10 | g. 25, –10 | h. 20, –10 | i. 15, –10 | j. 10, –10 |
A34(§). Modify eqs. (3.64) to use input and output temperatures in Fahrenheit and wind speeds in miles per hour. Calculate sufficient values to plot a graph similar to Fig 3.12 but in these new units.
A35. Find the heat index apparent temperature (°C) for an actual air temperature of 33°C and a relative humidity (%) of:
| a. 5 | b. 10 | c. 20 | d. 30 | e. 40 | f. 50 | g. 60 |
| h. 70 | i. 75 | j. 80 | k. 85 | m. 90 | n. 90 |
A36. Find the humidex apparent air temperature (°C) for an actual air temperature of 33°C and a dewpoint temperature (°C) of:
| a. 32.5 | b. 32 | c. 31 | d. 30 | e. 29 | f. 28 | g. 27 |
| h. 26 | i. 25 | j. 23 | k. 20 | m. 15 | n. 10 | o. 5 |
3.10.3. Evaluate & Analyze
E1. Assume that 1 kg of liquid water initially at 15°C is in an insulated container. Then you add 1 kg of ice into the container. The ice melts and the liquid water becomes colder. Eventually a final equilibrium is reached. Describe what you end up with at this final equilibrium?
E2. Explain in your own words why the units for specific heat Cp (J·kg–1·K–1) are slightly different than the units for the latent heat factor L (J·kg–1). (Hint: read the INFO box on Internal Energy.)
E3. Explain in your own words why the magnitude of Cp should be larger than the magnitude of Cv. (Hint: read the INFO box on Cp vs. Cv).
E4. Consider the INFO box on Cp vs. Cv, with Figure 3I.3c representing an initial state at equilibrium. Suppose you add some weight to the piston in Fig (c) causing the piston to become lower to reach a new equilibrium, but no thermal energy is added (∆q = 0). Describe what would happen to: (a) the molecules on average, (b) the gas temperature in the cylinder, (c) the air density in the cylinder, and (d) the air pressure in the cylinder.
E5. For the First Law of Thermodynamics (eq. 3.4d) which term(s) is are zero for a process that is:
| a. adiabatic | b. isothermal | c. isobaric |
E6. Start with eq. (3.4) and use algebra to derive equation (3.5). What did you need to assume to do this derivation? Does the result have any limitations?
E7. For Figure 3.2, speculate on other processes not listed that might affect the air-parcel temperature.
E8. Using Figure 3.3, explain in your own words the difference between a process lapse rate and an environmental lapse rate. Can both exist with different values at the same height? Why?
E9. Eq. (3.7) tells us that temperature of an adiabatically rising air parcel will decrease linearly with increasing height. In your own words, explain why you would NOT expect the same process to cause temperature to decrease linearly with decreasing pressure.
E10. If an air parcel rises isothermally (namely, heat is added or subtracted to maintain constant temperature), then what would happen to the potential temperature of the air parcel as it rises?
E11. Chinook winds (also known as foehn winds) consist of air descending down the lee slope of a mountain and then continuing some distance across the neighboring valley or plain. Why are Chinook winds usually warm when they reach the valley? (Hint: consider adiabatic descent of an air parcel.)
E12. In the definition of virtual potential temperature, why do liquid water drops and ice crystals cause the air to act heavier (i.e., colder virtual potential temperature), even though these particles are falling through the air?
E13. First make a photocopy of Figure 3.4, so that you can keep the original Thermo Diagram clean. a) On the copy, plot the vertical temperature profile for a standard atmosphere, as defined in Chapter 1. Suppose that this standard profile represents background environmental air.
b) On this same diagram, plat a point representing an air parcel at (P, T) = (100 kPa, 15°C). If you adiabatically lift this parcel to 50 kPa, what is its new temperature?
c) Is the parcel temperature a 50 kPa warmer or colder than the environment at that same pressure?
E14(§). For a standard atmosphere (see Chapt. 1), calculate potential temperature θ at z = 0, 2, 4, 6, 8, 10 km altitudes. Plot θ along the bottom axis and z along the vertical axis.
E15(§). Thermo diagrams often have many different types of lines superimposed. For example, on the background T vs. log-P diagram of Figure 3.4 is plotted just one type of line: the dry adiabats. Instead of these adiabats, start with the same background of a T vs. log-P diagram, but instead draw lines connecting points of equal height (called contour lines). To calculate these lines, use the hypsometric equation from chapter 1 to solve for P vs. (z, T). Do this for the z = 2, 4, 6, 8, 10 km contours, where for any one height, plug in different values of T to find the corresponding values of P that define the contour.
E16. For advection to be a positive contribution (i.e., causing heating) and for wind that is in a positive coordinate direction, explain why the corresponding temperature gradient must be negative.
E17. Suppose that mild air (20°C at 10 m altitude) rests on top of a warm ocean (26°C at the surface), causing convection (vertical overturning of the air). If there is no mean horizontal wind, then the effective heat flux at the surface has what value? Assume a mixed layer that is 1200 m thick with average thermodynamic state of r = 0.01 gvapor/gair and θ = 15°C.
E18. Light travels faster in warm air than in cold. Use this info, along with Figure 3.7, to explain why inferior mirages (reflections of the sky) are visible on hot surfaces such as asphalt roads. (Hint: Consider a wave front that is moving mostly horizontally, but also slightly downward at a small angle relative to the road surface, and track the forward movement of each part of this wave front — an optics method known as Huygens’ Principle. See details in the atmospheric Optics chapter.)
E19. Under what conditions would eqs. (3.34 - 3.35) be expected to fail? Why?
E20. Use eqs. (3.37) and (3.39) to solve for the heat flux as a function of the temperature difference.
E21. In Figure 3.8, the heat flux is greatest at the height where there is no change in the vertical temperature profile from before to after a storm. Why should that be the case?
E22. How fast does air temperature change if only if the only thermodynamic process that was active was direct IR cooling?
E23. In a thunderstorm, the amount of water condensation in the troposphere is often much greater than the amount of rain reaching the ground. Why is that, and how might it affect the heat budget averaged over the whole thunderstorm depth?
E24. Eq. (3.51) has what limitations?
E25. Comment on the relative strengths of advective vs. latent heating in an Eulerian system, given V = 5 m s–1, ∆T/∆y = –5°C/1000km, and 1 g/kg of water condenses every 5 minutes.
E26. Create a figures similar to Figure 3.9, but for:
a) daytime over a white concrete road,
b) nighttime black asphalt road.
E27. It is sometimes said that conductive heat flux into the ground is a response to radiative forcings at the surface. Is that statement compatible with the crude parameterization presented in this book for flux into the ground? Explain.
E28. What is the initial rate of change of average mixed-layer air temperature with horizontal distance downwind if the air is initially 5 °C colder than the water, given that the air blows over the water at speed 15 m s–1? Consider entrainment into the top of the mixed layer, but neglect other heating or cooling processes.
E29. Can the parameterizations (eqs. 3.58 - 3.61) actually give a balanced heat budget? For what types of situations are these parameterizations valid?
E30. (§). Suppose that we used the heat transfer eq. (3.35) as a basis for deriving wind chill. The result might be a different wind-chill relationship:
\(\ \begin{align} T_{\text {wind chill}} =T_{s}+\left(T_{\text {air}}-T_{s}\right) \cdot\left[b+a \cdot\left(\frac{M+M_{o}}{M_{o}}\right)^{0.16}\right]+T_{c}\tag{3.67}\end{align}\)
where Ts = 34.6°C is an effective skin temperature, and where, a = 0.5 , b = 0.62 , Tc = 4.2°C, and Mo = 4.8 km h–1. Plot this equation as a graph similar to Figure 3.12, and comment on the difference between the formula above and the actual wind-chill formula.
E31. Notice in Figure 3.12 that the curves bend the most for slow wind speeds. Why might you expect this to be the case?
3.10.4. Synthesize
S1. Describe the change to the ocean if condensation caused cooling and evaporation caused heating of the air. Assume dry air above the ocean.
S2. Suppose that zero latent heat was associated with the phase changes of water. Describe the possible changes to climate and weather, if any?
S3. Describe the change to the atmosphere if rising air parcels became warmer adiabatically while sinking ones became cooler.
S4. Suppose that for each 1 km rise of an air parcel, the parcel mixes with an equal mass of surrounding environmental air. How would the process lapse rate for this rising air parcel be different (if at all) from the lapse rate of an adiabatically rising air parcel (having no mixing).
S5. Macro thermodynamics (the kind we’ve used in this chapter) considers the statistical state of a large collection of molecules that frequently collide with each other, and how they interact on average with their surroundings. Can this same macro thermodynamics be used in the exosphere, where individual air molecules are very far apart (i.e., have a large mean-free path) and rarely interact? Why? Also, explain if how heat budgets can be used in the exosphere.
S6. Could there be situations where environmental and process lapse rates are equal? If so, give some examples.
S7. Suppose that the virtual potential temperature was not affected by the amount of solid or liquid water in the air. How would weather and climate change, if at all?
S8. The background of the thermo diagram of Figure 3.4 is an orthogonal grid, where the isotherms are plotted perpendicular to the isobars. Suppose you were to devise a new thermo diagram with the dry adiabats perpendicular to the isobars. On such a diagram, how would the isotherms be drawn? To answer this, draw a sketch of this new diagram, showing the isobars, adiabats, and isotherms. (Do this as a conceptual exercise, not by solving equations to get numbers.)
S9. Describe changes to Earth’s surface heat balance if the geological crust was 1 km thick aluminum (an excellent conductor of heat) covering the whole Earth.
S10. Suppose you were on a train moving in a straight line at constant speed. You make measurements of the surrounding environmental air as the train moves down the track.
a) If the environmental air was calm, do you think your measurements are Eulerian, Lagrangian, or neither? Explain.
b) If the environmental air was moving in any arbitrary speed or direction, do you think your measurements are Eulerian, Lagrangian or neither? Explain.
c) Try to create a heat budget equation that works in the framework, given your constant speed of translation of Mo.
S11. Describe how atmospheric structure, climate, and weather would change if the troposphere were completely transparent to all IR radiation, but was mostly opaque to solar radiation.
S12. Describe how errors in surface sensible and latent heat flux estimates would increase as the temperature and humidity differences between the two measurement levels approached zero.
S13. The wind-chill concept shows how it feels colder when it is winder. For situations where the wind chill is much colder than the actual air temperature, to what temperature will an automobile engine cool after it is turned off? Why? (Assume the car is parked outside and is exposed to the wind.)
Sample Application
[This sample applies to eqs. 3.1 and 3.3, but was put here on the last page of the chapter because there was no room for it earlier in the chapter.]
How much dew must condense on the sides of a can of soda for it to warm the soda from 1°C to 16°C?
Hints: Neglect the heat capacity of the metal can. The density of liquid water is 1000 kg·m–3. Assume the density of soda equals that of pure water. Assume the volume of a can is 354 ml (milliliters), where 1 l = 10–3 m3.
Find the Answer
Given: ρwater = 1000 kg·m–3.
Cliq = 4200 J·kg–1·K–1
Volume (Vol) in Can = 354 ml
Lcond = + 2.5x106 J·kg–1
∆T = 15 K
Find: Volume of Condensate
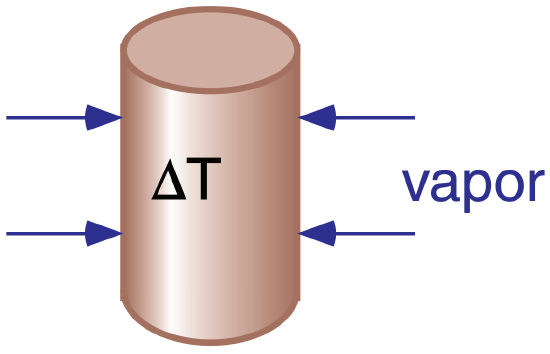
Equate the latent heat release by condensing water vapor (eq. 3.3) with the sensible heat gained by fluid in the can (eq. 3.1)
∆QE = ∆QH
ρcondensate· (∆Vol of Condensate)·Lcond = ρsoda· (Vol of Can)·Cliq·∆T
Assume the density of condensate and soda are equal, so they cancel. The equation can then be solved for ∆Volume of Condensate.
∆Volume of Condensate = (Vol of Can)·Cliq·∆T Lcond = (354 ml)·(4200 J·kg–1·K–1)·(15 K) (2.5x106 J·kg–1) = 8.92 ml
Check: Units OK. Sketch OK. Physics OK.
Exposition: Latent heats are so large that an amount of water equivalent to only 2.5% of the can volume needs to condense on the outside to warm the can by 15°C. Thus, to keep your can cool, insulate the outside to prevent dew from condensing.


