5.5: Curvature Effect - Kelvin Effect
- Page ID
- 3379
Let’s look at the curvature effect first (Figure \(\PageIndex1\)). Consider the forces that are holding a water drop together for a flat and a curved surface. The forces on the hydrogen bonding in the liquid give a net inward attractive force to the molecules on the boundary between the liquid and the vapor. The net inward force, divided by the distance along the surface, is called surface tension, \(σ\) with units of N/m or J/m2.

If the surface is curved, then the amount of bonding that can go on between any one water molecule on the surface and its neighbors is reduced. As a result, there is a greater probability that any one water molecule can escape from the liquid and enter the vapor phase. Thus, the evaporation rate increases. The greater the curvature, the greater the chance that the surface water molecules can escape. Thus, it takes less energy to remove a molecule from a curved surface than it does from a flat surface.
When we work through the math, we arrive at the Kelvin Equation:
\[e_{s c}(T)=e_{s}(T) \cdot \exp \left(\frac{2_{\sigma}}{n_{L} \cdot R \cdot T \cdot r_{d}}\right)\]
where esc is the equilibrium vapor pressure over a curved surface of pure water, es is the equilibrium vapor pressure over a flat surface of pure water, both of which are functions of temperature, although esc is also a function of the drop radius, nL is the number of moles per volume of water (55.5 moles L-1). R* is the molar gas constant, σ is the water surface tension, and r is the radius of the drop.
\[\left(\frac{2 \sigma}{n_{L} \cdot R^{*}}\right)=3.3 \times 10^{-7} \mathrm{m} K^{-1}\]
Since the evaporation is much, much greater over a curved surface, the condensation must also be much, much greater in order to keep condensation = evaporation, which is required for saturation (i.e., equilibrium). Thus, the saturation vapor pressure over a curved surface is much greater than the saturation vapor pressure over a flat surface of pure water. When we plot this equation, we get the plot in Figure \(\PageIndex2\):
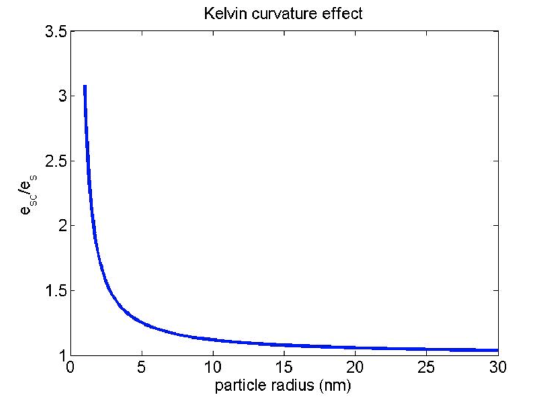
Note the rapid increase in equilibrium vapor pressure for particles that have radii less than 10 nm. Of course, all small clusters of water vapor and CCN start out at this small size and grow by adding water.
The Kelvin Equation can be approximated by expanding the exponential into a series:
\[e_{s c}(T)=e_{s}(T) \cdot\left(1+\frac{2 \sigma}{n_{L} \cdot R^{*} \cdot T \cdot r_{d}}\right)=e_{s}(T) \cdot\left(1+\frac{a_{K}}{r_{d}}\right), \quad\]
where
\[a_{K}=\frac{2 \sigma}{n_{L} \cdot R^{*} \cdot T}\]
Summary
Cloud drops start as very small spherical drops, but the vapor pressure required for them to form is much greater than es until they get closer to 10-2μm in size. The Kelvin effect is important only for tiny drops; it is important because all drops start out as tiny drops and must go through that stage. As drops gets bigger, their radius increases and esc approaches es.
So, is it possible to form a cloud drop out of pure water? This process is called homogeneous nucleation. The only way for this to happen is for two molecules to stick together, then add another, then another, etc. But the radius of the nucleating drop is so small that the vapor pressure must be very large. It turns out that drops probably can nucleate at a reasonable rate when the relative humidity is about 440%. Have you ever heard of such a high relative humidity?
So, the lesson here is that homogeneous nucleation is very unlikely because of the Kelvin effect.


