9.3: Five Air Motion Types You Must Get to Know
- Page ID
- 3406
Generally, air velocities change with distance in such a way that more than one partial derivative is different from zero at any time. It turns out that any motion of an air parcel is a combination of five different motions, one being translation, which we have already discussed, and four of which can be represented by pairs of partial derivatives of velocity. Of these four, one is a deformation of the air parcel, called stretching, which flattens and lengthens the air parcel. A second is another deformation of the air parcel, called shearing, which twists the air parcel in both the x and y directions. A third is pure rotation, called vorticity. A fourth enlarges or shrinks the parcel without changing its shape, called divergence. Let’s consider each of five types of air motion alone, even though more than one is often occurring for an air parcel.
Translation simply moves the air parcel without stretching it, shearing it, rotating, or changing its area. There are no partial derivatives of velocities involved with translation.
For the remaining four cases, we will provide examples in which the motion (stretching, shearing, vorticity, and divergence) has a positive value. We could have provided examples in which the motion has negative value, but the conclusions would be the same.
Stretching deformation is represented by \(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\),
u gets more positive as xgets more positive and u gets more negative as x gets more negative (so that the derivative is always positive), making the parcel grow in the x direction. In the other direction, v gets more negative as y gets more positive and v gets more positive as y gets more negative (so that the derivative is always negative), making the parcel shrink in the y direction (see figure below). However, the total area of the air parcel will remain the same if \(\partial u / \partial x=\partial v / \partial y\). Shown in the figure is positive stretching deformation; negative stretching deformation occurs when the parcel is stretched in the y direction.
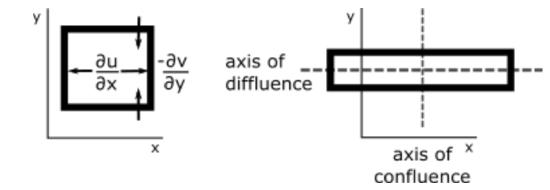
Credit: W. Brune
Shearing deformation is represented by \(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\). In this case, v gets more positive as x gets more positive and v gets more negative as x gets more negative, resulting in the air parcel part at lower x getting pushed towards lower y, and the air parcel part at higher x getting pushed towards higher y. At the same time, u gets more positive as y gets more positive and u gets more negative as y gets more negative, resulting in the air parcel part at lower ygetting pushed to lower x and the air parcel part at higher y getting pushed to higher x (see figure below). The total area of the air parcel remains the same after the shearing occurs. Shearing deformation is positive when the air parcel stretches in the southwest/northeast direction and contracts in the southeast/northwest direction (as in the figure below). Shearing deformation is negative when the parcel stretches in the southeast/northwest direction and contracts in the southwest/northeast direction.
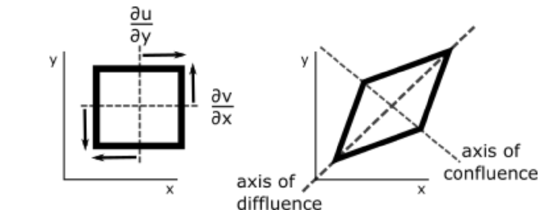
Credit: W. Brune
As the two figures above show, both stretching and shearing deformation cause stretching along the axis of diffluence and contraction along the axis of confluence, with the two axes at right angles to each other. These deformations result in weather fronts. In both cases, these motions cause some parts of the air parcel to move away from each other and some parts of the air parcel to move towards each other. The air coming together is called frontogenesis.
Vorticity is represented by \(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial v} \equiv \zeta\). Vorticity is special, and because it is special, it is represented by a Greek lower-case letter, zeta (ζ). In this case, the air parcel does not get distorted if \(\partial v / \partial x=-\partial u / \partial y\) and does not change area. It simply rotates (see figure below).

Credit: W. Brune
This difference in partial derivatives may look familiar to you.
\[\vec{U}_{H}=\vec{i} u+\vec{j} v \quad\) and \(\quad \vec{\nabla}_{H}=\vec{i} \frac{\partial}{\partial x}+\vec{j} \frac{\partial}{\partial y}\]
\[\vec{\nabla}_{H} \times \vec{U}_{H}=\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) \vec{k}\]
\[\zeta=\vec{k} \cdot\left(\vec{\nabla}_{H} \times \vec{U}_{H}\right)\]
Vorticity is actually a vector that follows the right-hand rule. Your fingers curve in the direction of the flow and your thumb is the vorticity vector. Here we are discussing only the vertical component of the vorticity. In a right-handed coordinate system, counter-clockwise flow in the x-y plane will result in your thumb pointing in the positive z direction. Hence, vorticity is positive if the rotation is counter-clockwise and is negative if the rotation is clockwise. In the Northern Hemisphere, low-pressure systems are typically characterized by counter-clockwise flow and thus have positive vorticity whereas high-pressure systems are typically characterized by clockwise flow and thus have negative vorticity. The vorticity definition is the same in the Southern Hemisphere (with counter-clockwise flow being positive and clockwise flow being negative), but low-pressure systems usually have clockwise flow and high-pressure systems usually have counterclockwise flow. Vorticity is an important quantity because low- and high-pressure systems are responsible for a lot of weather.
Divergence is represented by \(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} \equiv \delta\).
Divergence is also special, and because it is special, it is represented by a Greek lower-case letter, delta (δδ ). When the divergence is positive, the air parcel grows (i.e., its area increases) (see figure below). If the divergence is negative, then the air parcel shrinks (i.e., its area decreases). Strictly speaking, δδ is the horizontal divergence because it describes a change in parcel area projected onto a horizontal plane. Adding ∂w/∂z to the horizontal divergence gives the 3-D divergence.
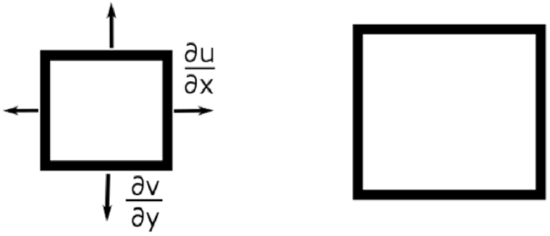
Divergence of an air parcel shown for the case when \(\partial u / \partial x\) and \(\partial v / \partial y\) are both positive.
Credit: W. Brune
The divergence can be written in vector notation:
\[\vec{U}_{H}=\vec{i} u+\vec{j} v \quad\) and \(\quad \vec{\nabla}_{H}=\vec{i} \frac{\partial}{\partial x}+\vec{j} \frac{\partial}{\partial y}\]
\[\vec{\nabla}_{H} \cdot \vec{U}_{H}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\]
Watch this video (1:56) for further explanation:
Five Air Motion Types
- Click here for transcript of the Five Air Motion Types video.
-
Airflow can be characterized by a combination of five basic flow types. Translation, which is just a motion of the air parcel, no change in area. Stretching deformation, which increases the parcel in one direction and decreases it in another. Shearing deformation, which shears the air parcel simultaneously in the x and y directions, creating a diamond shape out of a square. Vorticity, which thins the air parcel. And divergence, which grows the air parcel. The last four types can be represented by combinations of the partial derivatives of horizontal velocities, u and v, with respect to horizontal directions, x and y. Note that if we know the wind velocity vectors in the [INAUDIBLE] grid then we can calculate these five wind types for an airflow by determining the changes in the velocities as functions of x and y. And then combining these differentials that are shown here to find the actual values for stretching deformation, shearing deformation, vorticity, and divergence. The units for all of these motion types is per second, which is a frequency. In the figures, I have shown only those transformations that are positive. Negative translation goes to the left. Negative stretching deformation elongates the parcel in the y direction. Negative sharing deformation elongates the parcel in the northwest-southeast direction. Negative vorticity is clockwise. Negative divergence causes the air parcel to shrink, which is called convergence. Prove it to yourself that these transformations shown here are all possible. We will use the divergence heavily in the next section to the lesson.


