13.3.2: Packing in Three Dimensions

In three dimensions, marbles (or anions) can be closest packed in two ways. Both are equivalent to piling hexagonal packed sheets one above another. Three adjacent marbles in a hexagonal closest-packed sheet make a triangle. If we put another marble on top of them, it slips into the low spot above the center of the triangle, resulting in a tetrahedral structure composed of four marbles (Figure 13.12a). All four marbles touch each other, so the arrangement is closest packed. Alternatively, we could put three marbles on top of the first three, as shown in Figure 13.12b. This arrangement of marbles, too, is closest packed. Each marble is in contact with three in the adjacent layer but you may have to look closely to convince yourself that this is the case.

Figure 13.12: Closest packing in three dimensions

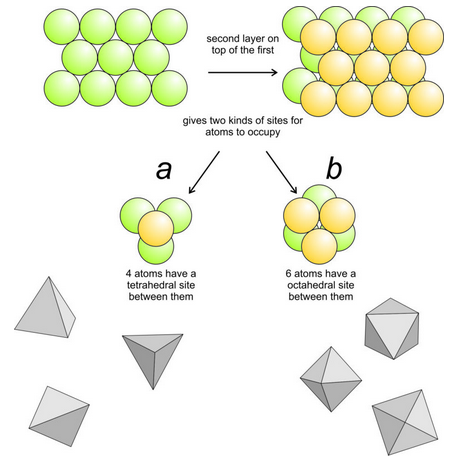
Figure 13.12a shows four marbles, or four cations, forming a tetrahedron. If an anion is between them, it will be in tetrahedral coordination. Figure 13.12b shows 6 marbles, or cations, forming an octahedron. If an anion is between them, it will be in octahedral coordination. The geometric shapes in the bottom of Figure 13.12 are different views of tetrahedra and octahedra created by joining the centers of the anions.

Figure 13.13: Hexagonal closest packing and cubic closest packing

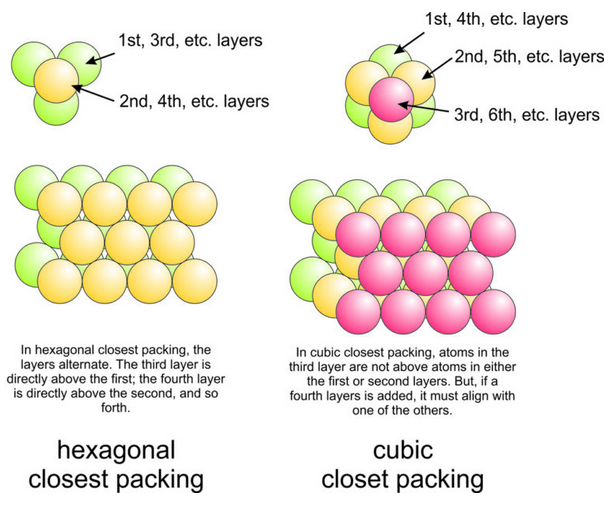
Now consider an entire layer of hexagonal packed marbles. If we put another hexagonal packed layer on top, its marbles naturally fall into gaps produced by groups of three in the bottom layer. So the marbles in the second layer will not be directly above those in the first (Figure 13.13).

If we now place a third layer on top of the second, marbles will fill gaps as before. However, marbles in the third layer may or may not be directly above those in the first layer. There are two possibilities (Figure 13.13). If the third layer is above the first layer, we call the structure hexagonal closest packed. If the layer is not, we call it cubic closest packed (see Box 13-3, below). Although it may not be immediately obvious, if we add a fourth layer, its marbles must lie directly above those of another layer.

We can describe hexagonal closest packed (HCP) structures as having ABABAB layering because alternate layers are directly above each other. Cubic closest packed (CCP) structures have an ABCABCABC packing sequence; it takes three layers before they repeat. In both HCP and CCP, every marble (or anion) is in contact with 12 others.

Why Are Atomic Arrangements Called Hexagonal Closest Packed (HCP) and Cubic Closest Packed (CCP)?

Figure 13.14: Three ways atoms can pack together

In two dimensions, closest-packed atoms are in hexagonal patterns. Each atom is surrounded by six others with no wasted space between. In 3D closest-packed structures, each atom is surrounded by 12 others with no wasted space between.

3D closest packed arrangements may be hexagonal closest packed (HCP) or cubic closest packed (CCP). If HCP, atoms from alternating layers yield a unit cell with the shape of a hexagonal prism. If CCP, atoms from four layers combine to form a unit cell with the shape of a cube. The large drawings in Figure 13.14 show two different views of three structures. The drawings on the left show packing more clearly, but the drawings on the right (with much smaller atoms) do a better job of revealing atom locations.

Hexagonal closest packing involves two layers of atoms that alternate – even-numbered layers are directly above/below each other, and odd-numbered layers are directly above/below each other (but are offset with respect to the even-numbered layers). Figure 13.14a shows an example of an HCP arrangement. The bottom and top (orange) layers of seven atoms are identical; they are in a hexagonal pattern with an extra atom at the center. The middle layer (green) contains three touching atoms forming an equilateral triangle. The three nestle snugly above and below openings in the bottom and top layers.

The drawing of cubic closest packing (Figure 13.14b) is a bit more difficult to see. 14 atoms form a cubic unit cell. The arrangement contains three layers that repeat. The blue atom in the top right corner is in a layer by itself. Behind it, the six orange atoms form a closest packed triangle. Behind them, six green atoms also form a closest packed triangle, but with a different orientation. And, behind them is another single blue atom. So, the layers are sloping instead of horizontal or vertical. The inset shows the layers rotated to be horizontal.

Although the closest packing model is a convenient concept, most minerals do not have atoms in closest-packed arrangements. Some halide and sulfide minerals have nearly closest packed structures, but metal crystals are the best examples. Gold, silver and platinum are examples of native metals with cubic closest packing. Magnesium and zinc are examples of native metals with hexagonal closest packing. Native iron has atoms with a body-centered cubic arrangement (Figure 13.14c) with atoms at the corners and one in the center. This arrangement, however, is not closest packed.