13.3.1: Closest Packing in Two Dimensions

Last updated
Save as PDF

Page ID: 18347

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

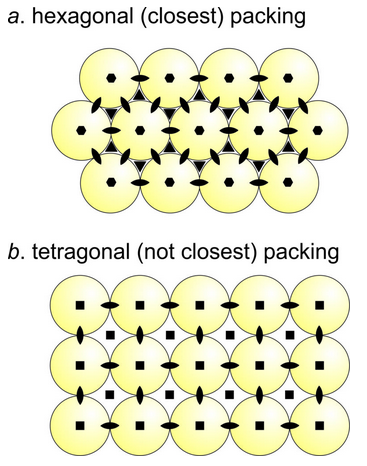
13.11.png — Figure 13.11: Packing of ions in 2D

In many crystals, anions pack together in highly regular repetitive patterns. As an analogy, consider a collection of equal-sized marbles. We may arrange the marbles so rows line up and repeat at regular spacing characterized by translational symmetry. Figure 13.11 shows two alternative ways that marbles (shown as circles) can pack together in two dimensions. In Figure 13.11a groups of three marbles are arranged so that connecting their centers yields an equilateral triangle. On a slightly larger scale, each marble is surrounded by six others, and connecting their centers makes a hexagon. The total pattern has 2-fold, 3-fold, and 6-fold rotational symmetry (shown by symmetry symbols in the drawing), and also translational symmetry and mirror planes. Figure 13.11b shows an alternative arrangement of marbles in two dimensions. This arrangement has 2-fold and 4-fold axes of symmetry (shown by lens- and square-shaped symbols), but not 3-fold. The symmetries of the two patterns in Figure 13.11 are equivalent to the symmetries of a hexanet and a square net (Figures 11.23 and 11.27 in Chapter 11).

We call the arrangement of marbles in Figure 13.11a hexagonal packing. We call the pattern in Figure 13.11b tetragonal packing because of the obvious 4-fold symmetry. In hexagonal packing the marbles are closer together than in tetragonal packing. Because no other two-dimensional arrangement allows marbles to be closer together, we say the hexagonal arrangement is closest packed. Each marble touches six others, the maximum possible. In the tetragonal arrangement, each marble only touches four others.