11.8.2: Points in Unit Cells

Last updated
Save as PDF

Page ID: 18454

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

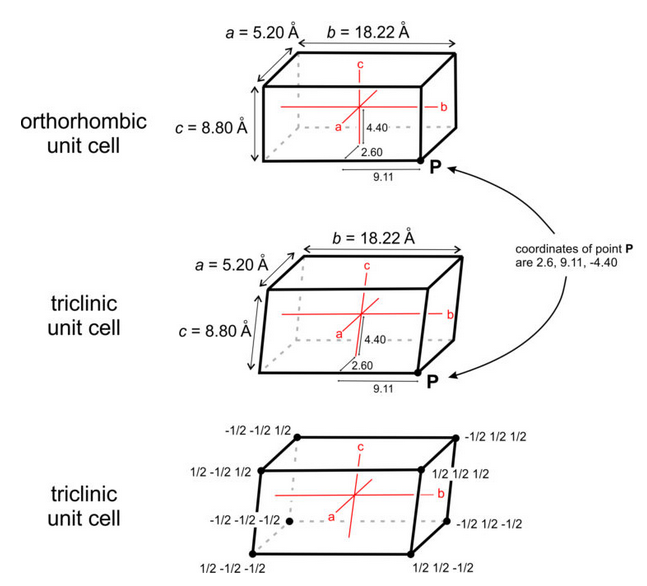
11.59.png — Figure 11.59: Coordinates of points in unit cells

Mineralogists describe the locations of atoms or other points in unit cells by giving their coordinates. As examples, consider the orthorhombic and triclinic crystals shown in Figure 11.59. In the orthorhombic crystal the three axes (shown in red) intersect at 90°, in the triclinic crystal they do not. Assume both crystals have cell dimensions a = 5.20 Å, b = 18.22 Å, and c = 8.80 Å, and the axes’ origins are at the center of the unit cells as shown. The coordinates of point P, at the lower right-hand corner in drawings a and b, are therefore 5.20/2 = 2.60 Å, 18.22/2 = 9.11 Å, and 8.80/2 = -4.40 Å. The negative sign arises because the points are in a negative direction from the origin along the c-axis.

We do not, however, normally report coordinates in angstroms (Å). Instead, we report distances relative to unit cell dimensions. Another way to describe the location of point P in Figure 11.59a and b would be to say it has coordinates 1/2a, 1/2b, -1/2c. Typically, we normalize coordinates to unit cell dimensions by dropping the a, b, and c. The coordinates then become 1/2 , 1/2 , -1/2. The points at the corners must have coordinates ±1/2, ±1/2, ±1/2, if the origin is at the center of the unit cell (Figure 11.59c). Note that the system to which a crystal belongs does not affect coordinate values.

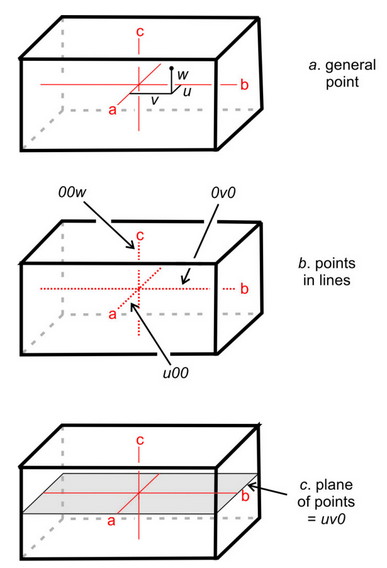
11.60.png — Figure 11.60: General points and special points in unit cells

Traditionally, crystallographers have used the variables u, v, and w to represent the coordinates of a point if the coordinates are rational numbers, and x, y, and z if irrational. For simplicity, in this text we will use uvw in all instances (Figure 11.60a). We can say that uvw represents a general point anywhere in the cell.

Suppose two coordinates, for example v and w, are zero. All the points described by the coordinates u00 constitute a set of special points, lying along the a-axis (Figure 11.60b). Similarly, 0v0 and 00w refer to sets of special points on the b- and c-axes, respectively. If only one coordinate equals zero, a point lies in a plane including two axes. We might, for example, talk about special points located at uv0. These are points on a plane that includes the a- and b-axes, as shown in Figure 11.60c. Note that no parentheses or brackets are used when giving coordinates of a point.

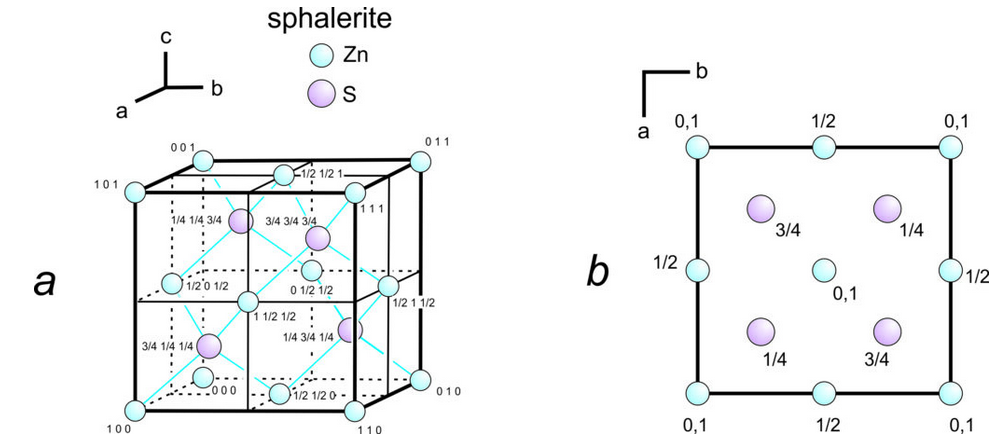
11.61.png — Figure 11.61: The atoms in a sphalerite unit cell

Figure 11.61a shows a unit cell of sphalerite, ZnS, with uvw coordinates for each atom. The axes origin is in the bottom back left corner. Because three-dimensional drawings are sometimes difficult to draw and see, crystallographers often use projections, which contain the same information in a less cluttered manner (Figure 11.61b). In the projection, which is a view down the c-axis, we need not specify u and v values because they can be estimated from the location of the atoms in the drawing. The numbers are w values. Sometimes we omit w values for atoms at unit cell corners; by convention, this means the atoms are found on both the top and bottom of the cell as it appears in projection.