11.8.1: Unit Cell Parameters and Crystallographic Axes

Last updated
Save as PDF

Page ID: 18453

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

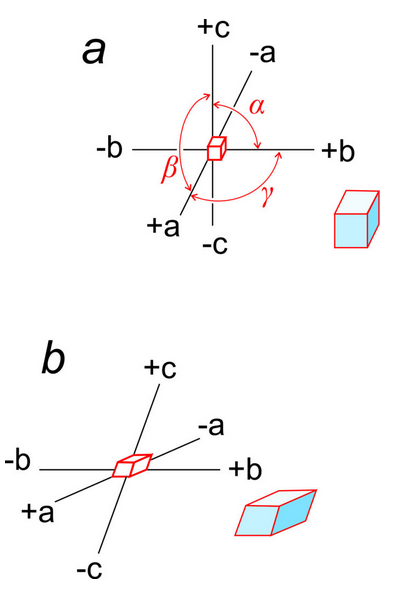
11.56.png — Figure 11.56: Coordinate systems from mineral crystals

Earlier in this chapter, we introduced the unit cell parameters a, b, c, α, β, and γ. a, b, and c are the lengths of unit cell edges; α, β, and γ are the angles between the edges. α is the angle between b and c, β is the angle between a and c, and γ the angle between a and b (Figure 11.56a).

Unit cell edges define a coordinate system used by crystallographers when they wish to describe the locations of atoms or other features within a cell. Some crystal systems are orthogonal (cubic, tetragonal, orthorhombic) but others are not. Cubic crystals, and others that belong to an orthogonal system, use a standard Cartesian coordinate system. Figure 11.56a shows an example.

Figure 11.56b shows axes that are inclined with respect to each other. In this example, they correspond to a triclinic unit cell. α, β, and γ, the angles between axes, are not equal to 90^o and (in contrast with the cube) the edges of the unit cell have different lengths along different axes.

Figure 11.57 shows coordinate axes for each of the crystal systems. We have labeled all angles in the top drawing (of a green cube); in the other drawings, only the non-90^o angles are identified. In the orthogonal systems, α, β, and γ all equal 90^o. In the hexagonal and rhombohedral systems, β = 120^o and the other angles are 90^o. Other constraints are in the right-hand column of this figure. We used calcite as an example of a rhombohedral mineral. In much of the literature, however, calcite’s unit cell is described using a hexagonal prism.

11.57.png — Figure 11.57: Coordinate systems for different crystal systems

Although it makes no practical difference which edges of a unit cell we call a, b, or c, or which angles are α, β, and γ, mineralogists normally follow certain conventions. In triclinic minerals, none of the angles are special and a, b, and c are all different lengths. Although the literature contains exceptions, by modern convention edges are chosen so that c < a < b. In monoclinic minerals, such as sanidine, only one angle in the unit cell is not 90°. By convention, the non-90° angle is β, the angle between a and c. For historical reasons, this convention is called the second setting for monoclinic minerals. In orthorhombic crystals, we choose axes so that c > a > b. In tetragonal and hexagonal crystals, the c-axis always corresponds to the 4-fold or 6-fold axis.

In this book we use a, b, and c to designate the three crystallographic axes, but crystallographers sometimes use subscripts to indicate axes, and thus cell edges, that must be identical lengths because of symmetry. Instead of a, b, and c, the three axes of cubic minerals might be designated a₁, a₂, and a₃. The axes of tetragonal crystals can be designated a₁, a₂, and c.

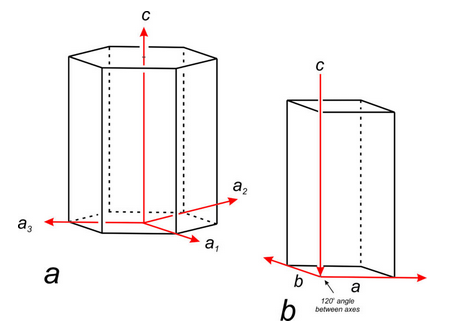
11.58.png — Figure 11.58: Two choices for axes in hexagonal crystals

For hexagonal crystals, crystallographers have historically used four axes: a₁, a₂, a₃, and c (Figure 11.58a). The three a-axes, a₁, a₂, and a₃, are parallel to edges of a nonprimitive hexagonal unit cell. Although the third a-axis is redundant for describing symmetry or points in 3D space, it has been included in the past to emphasize that there are three identical a-axes perpendicular to the c-axis. Because only three axes are used in much of the modern literature (Figure 11.58b), we will only briefly mention the fourth axis in the rest of this chapter.

Although mineralogists historically used angstroms (1 Å = 10^-10m) to give cell dimensions, much recent literature uses nanometers (1 nm = 10 Å). Typical mineral unit cells have edges of 2 to 20 Å (0.2 to 2 nm). The angles α, β, and γ are normally given as a decimal number of degrees (for example, 94.62°). These angles between edges vary greatly, although unit cells are often chosen so that angles are close to 90°.

Instead of using angstroms (or nanometers) to give distances, we may also use unit cell dimensions as a scale. For example, we might say that a certain plane intersects the axes at distances of 3a, 2b, and 2c from the origin. It is implicit that 3a refers to a distance equal to three unit cell edge lengths along the a-axis, 2b a distance equal to two unit cell lengths along the b-axis, and 2c a distance equal to two unit cell lengths along the c-axis.

The symmetry of a unit cell always affects the relationships between a, b, and c. So, in the cubic system, a = b = c, but in the tetragonal and hexagonal systems a = b ≠ c. The relationships implied by crystal systems mean that, for systems other than triclinic, we need not give six values to describe unit cell shape. For example, for orthorhombic, hexagonal, tetragonal, and cubic minerals, we do not specify any angles because they are all defined by the crystal system. The table below gives examples of unit cell parameters for minerals from each of the crystal systems; unnecessary information has been omitted. These same example minerals are the ones listed in Figure 11.57.

Unit Cell Parameters (a, b, c, α, β, and γ), Z (number of formulas per unit cell), and V (unit cell volume) for One Mineral from Each of the Crystal Systems*
fluorite CaF₂	rutile TiO₂	beryl Be₃Al₂Si₆O₁₈	calcite CaCO₃	enstatite Mg₂Si₂O₆	sanidine KAlSi₃O₈	albite NaAlSi₃O₈
cubic Z = 4 a = 5.46 V = 162.77	tetragonal Z = 2 a = 4.59 c = 2.96 V = 62.36	hexagonal Z = 2 a = 9.23 c = 9.19 V = 2034.09	rhombohedral Z = 2 a = 4.98 c = 17.06	orthorhombic Z = 4 a = 18.22 b = 8.81 c = 5.21 V = 836.30	monoclinic Z = 4 a = 8.56 b = 13.03 c = 7.17 γ = 115.98 V = 799.72	triclinic Z = 4 a = 8.14 b = 12.8 c = 7.16 α = 94.33 β = 116.57 γ = 87.65 V = 746.01
*a, b, and c are in angstroms; α, β, and γ are in degrees; and V is in cubic angstroms.

Consider the triclinic mineral albite, a feldspar with composition NaAlSi₃O₈. The last column in the table lists albite’s unit cell parameters. Because none of the angles are special and none of the cell edges are equal, we need six parameters to describe the cell shape. In contrast, fluorite (the first column of the table) has a cubic unit cell, so we need to give only one cell dimension, the length of the cell edge. It is implicit that all angles are 90° and all cell edges are the same length.

Physical dimensions do not completely describe a unit cell. We must also specify the nature and number of atoms within the unit cell. To provide some of this information, the table above lists two other things besides dimensions and angles: mineral formulas and Z, the number of formulas in each unit cell. For example, fluorite has the formula CaF₂ and Z = 4. This means there are 4 CaF₂ molecules (4 Ca and 8 F atoms) in each unit cell. Albite has the formula NaAlSi₃O₈ and Z = 4. This means that four NaAlSi₃O₈ formulas are in each unit cell. In other words, each unit cell contains 4 Na atoms, 4 Al atoms, 12 Si atoms, and 32 O atoms.