11.4.2: Unit Cell Symmetry and Crystal Symmetry

Consider fluorite (CaF₂), spinel (MgAl₂O₄), the garnet almandine (Fe₃Al₂Si₃O₁₂), and the rare mineral tetrahedrite (Cu₁₂As₄S₁₃). Tetrahedrite has a primitive cubic unit cell; fluorite and spinel have face-centered cubic unit cells; almandine has a body-centered cubic unit cell. In fluorite, Ca²⁺ is found at the corners of the unit cell and at the center of each face, while F^–occupies sites completely within the unit cell (see Figure 11.6). Spinel, almandine, and tetrahedrite have more complex structures, in large part because they contain more than one cation.

Many unit cells together make up a crystal. The crystal may or may not have the same symmetry as a single unit cell. In fluorite, spinel, and almandine crystals, unit cells stack together so that all symmetry elements (rotation axes and mirror planes) are preserved. However, fluorite crystals are typically cubes, spinel crystals are typically octahedra, and almandine crystals are typically dodecahedra. Figure 11.38 shows how cubes can combine to make these shapes. Figure 11.38e shows an example of a crystal, made with a cubic unit cell, that contains two forms (two differently shaped kinds of faces).

Figures 11.39 through 11.42 show mineral examples. We also saw a beautiful dodecahedral garnet crystal in Figure 10.48 (Chapter 10) and well formed fluorite crystals in Figures 4.3 and 4.37 (Chapter 4). The cube, octahedron, and dodecahedron are all special forms that have the same symmetry as the unit cell, ⁴/_m3²/_m. Tetrahedrite crystals (Figures 11.36d and 11.40), in contrast with the other three, do not have the same symmetry as their unit cell. Although made of cubic unit cells, the crystals lack 4-fold rotation axes. Instead, when euhedral, tetrahedrite crystals typically form pyramids that have symmetry 43m. See the drawing in Figure 11.38, below.

Figure 11.38: Cubic unit cells combining to make crystals

Figure 11.39: Fluorite cubes with specks of pyrite on top

Figure 11.40: Spinel octahedra in a white calcite marble

Figure 11.41: Garnet in a schist from Alaska

Figure 11.42: Tetrahedrite with minor malachite and azurite

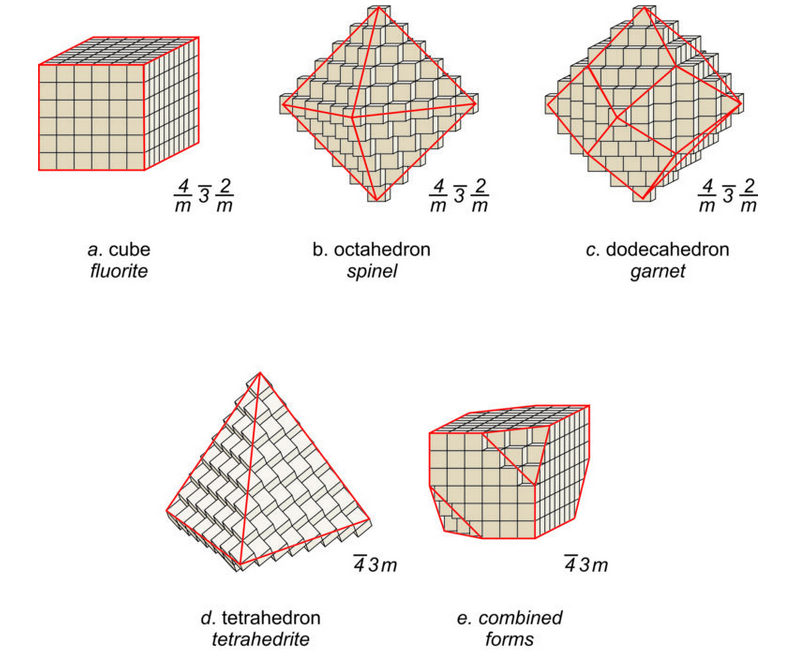
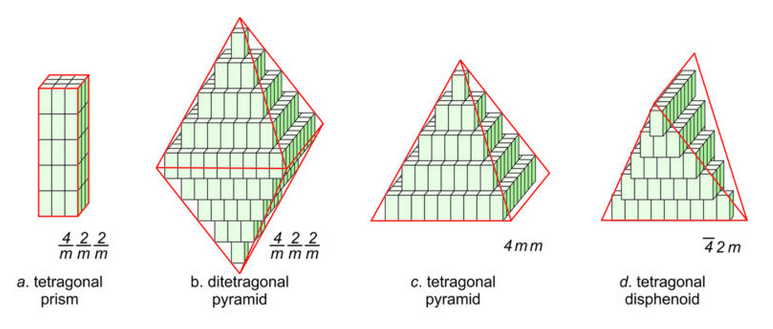
Figure 11.43 shows how tetragonal unit cells can be stacked to produce crystals. The results include a tetragonal prism and a ditetragonal pyramid that have the same symmetry as the unit cell (⁴/_m²/_m²/_m). But tetragonal unit cells can also create a pyramid (with symmetry 4mm) or a tetragonal disphenoid (with symmetry 42m). Other shapes with other symmetries are possible too. Note that the crystal in Figures 11.41b and d contain a single form (al faces are the same shape); the other two crystals contain two forms.

Figure 11.43: Four crystals composed of tetragonal unit cells

The preceding discussion points out a fourth important law of crystallography is:
blank■ If a crystal has certain symmetry, the unit cell must have at least as much symmetry.

As a corollary to this law, because crystals consist of unit cells, the symmetry of a crystal can never be more than that of its unit cell. If a crystal has a 4-fold axis of symmetry, it must have a unit cell that includes a 4-fold axis of symmetry. A mineral that forms cubic crystals must have a cubic unit cell. If a crystal has certain symmetry, it is certain that the unit cell and crystal’s atomic structure have at least that much symmetry. They may have more, as in the case of tetrahedrite.

This fourth law is the basis for the crystal systems we introduced in the previous chapter. The symmetry of a crystal requires certain symmetry in the crystal’s unit cell. And we divide the 32 possible symmetries – the 32 point groups – into systems based on that understanding. The six crystal systems are defined by symmetry and named by their unit cell shape. And crystals in the same crystal system all have the same-shaped unit cells, even if the crystals themselves do not look the same.

If, for example, a crystal has symmetry 4, 4, ⁴/_m, 422, 4mm, 42m, or ⁴/_m²/_m²/_m, it must have a unit cell that is a tetragonal prism. If a crystal has symmetry 222, mm2, or mmm, it must have a unit cell that is an orthorhombic prism, and so forth. The table below summarizes these relationships. By examining a crystal’s morphology, we can often determine the point group, system, and unit cell shape. Determining whether a unit cell is primitive, face-centered, body-centered, or end-centered, however, is not possible without additional information, which usually comes from X-ray diffraction studies.

Crystal Systems and Point Groups
crystal system	unit cell shape	point groups
triclinic	triclinic prism	1, 1
monoclinic	monoclinic prims	2, m, ^2/m
orthorhombic	orthorhombic prism	222, mm2 , mmm
tetragonal	tetragonal prism	4, 4, ^4/m, 422, 4mm, 42m, ^4/m^2/m^2/m
rhombohedral	rhombohedron	3, 3, 32, 3m, 3 m
hexagonal	hexagonal prism	6, 6, ^6/m, 622, 6mm, 62m, ^6/m^2/m^2/m
cubic	cube	23, ^2/m3, 432, 43m, ^4/m3^2/m

It is important to remember that the symmetry of a crystal depends not only on the symmetry of the unit cell, but also on how the unit cells combine to make the crystal. Some minerals, such as halite and other salts, tend to develop euhedral crystals with obvious symmetry, making it easy to infer the symmetry of the unit cell. Others develop crystals with faces that are nearly identical, suggesting the presence of symmetry but leaving some uncertainty. While size and shape of faces can vary because of accidents of crystal growth, the angles between faces vary little from the ideal (Steno’s law). Consequently, crystallographers often rely on angles instead of face shapes to infer the symmetry of the unit cell. Even if a crystal is anhedral and poorly formed, its internal structure is orderly and its unit cells all have the same atomic arrangement.