11.2: Translational Symmetry
- Page ID
- 17555
In the previous chapter we discussed symmetry due to rotation, reflection, and inversion. These are all types of point symmetry. The orderly repetition of patterns due to translation is another form of symmetry, called space symmetry. Space symmetry differs from point symmetry.
Space symmetry repeats something an infinite number of times to fill space, while point symmetry repeats something a discrete number of times and only describes symmetry localized about a central point. Point symmetry operators return a dot or a crystal face to its original position and orientation after 1, 2, 3, 4, or 6 repeats of the operation, but space symmetry operators do not. Translation goes on (almost) forever!
We often envision translational symmetry by thinking about a lattice, a set of an infinite number of points related by translations. In two dimensions, a lattice is called a plane lattice. In three dimensions, a lattice is a space lattice. Whether two or three dimensional, lattices are imaginary – they are not physical entities – they are patterns that we use to describe translational symmetry.
Figure 11.14a shows an example of how we depict a plane lattice. The vectors t1 and t2 are translation operators that generate the entire lattice from a single starting point. This drawing only shows part of the lattice; in your mind you should picture it extending infinitely in all directions.
Translational symmetry, like all symmetry, is a property that objects may have. If we have an object or a drawing, we can describe its translational symmetry. But it does not work the other way around because many different objects or drawings may have identical symmetry.
For example, Figure 11.14b (above) shows cats related by the same symmetry depicted in Figure 11.14a. Figure 11.14c shows parallelograms related by the same symmetry. And Figure 11.14d shows colored circles (that might represent atoms) related by the same symmetry.
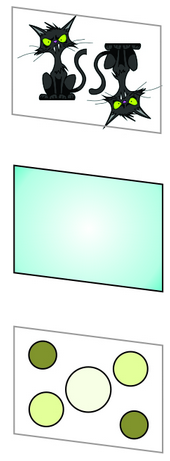
The four drawings in Figure 11.14 have more than just translational symmetry. They also contain multiple 2-fold rotation axes perpendicular to the plane of the page. And there are inversion centers, too. So we see that translational symmetry can combine with other kinds of symmetry.
Repetitive patterns are composed of motifs, which are designs that repeat, such as a flower pattern that might be on wallpaper. The term motif is used in an analogous way in music to refer to a sequence of notes that repeat. Interior decorators or clothing designers use the term to describe a common theme or element in their work.
A motif (whether it comprises two cats, a parallelogram, or colored circles) and empty space around it, make up unit cells that repeat to create an infinite pattern. The lattice describes the nature of the repetition, with each lattice point representing one motif. But lattice points do not correspond to any particular point on a motif. We could choose them at the motif’s center or one of its corners and the result would be the same.
Figure 11.15 shows unit cells that can be used to generate the patterns seen in Figure 11.14. These unit cells are parallelograms with dimensions and angles that match the translation vectors of the lattice. Notice that each one of these unit cells has a 2-fold axis of symmetry perpendicular to the page and an inversion center. This symmetry must be present to be consistent with the lattice.