11.1: Observations in the Seventeenth through Nineteenth Centuries

In 1669 Nicolaus Steno studied many quartz crystals and found angles between adjacent prism faces, termed interfacial angles, to be 120^o no matter how the crystals had formed. For example, Figures 11.2 to 11.5 show four varieties of quartz with nearly identical crystal shapes and similar angles between faces. Steno could not make precise measurements, and some of his contemporaries argued that he was overlooking subtle differences.

Figure 11.2: Citrine from Minas Gerais, Brazil

Figure 11.3: Amethyst from Veracruz, Mexico. The specimen is 5.8 cm wide.

Figure 11.4: Smoky quartz from near Roswell, New Mexico

Figure 11.5: Phantom quartz from Minas Gerais, Brazil. The photo is 7.8 cm tall.

A century after Steno, in 1780, more accurate measurements became possible when Arnould Carangeot invented the goniometer, a protractor-like device used to measure interfacial angles on crystals. Carangeot’s measurements confirmed Steno’s earlier observations. Shortly after, Romé de l’Isle (1782) stated the first law of symmetry, a law called the constancy of interfacial angles, which we commonly call Steno’s law. This law states that:
blank■ Angles between equivalent faces of crystals of the same mineral are always the same.

Steno’s law acknowledges that the size and shape of the crystals may vary.

In 1784 René Haüy studied calcite crystals and found that they had the same shape, no matter what their size. Haüy hypothesized the existence of basic building blocks called integral molecules and argued that large crystals formed when many integral molecules bonded together. Haüy erroneously concluded that integral molecules formed basic units that could not be broken down further. At the same time, Jöns Jacob Berzelius and others established that the composition of a mineral does not depend on sample size. And Joseph Proust and John Dalton proved that elements combined in proportions of small rational numbers. Scientists soon combined these crystallographic and chemical observations and came to several conclusions:
blank• Crystals are made of small basic building blocks.
blank• The blocks stack together in a regular way, creating the whole crystal.
blank• Each block contains a small number of atoms.
blank• All building blocks have the same atomic composition.
blank• The building block has shape and symmetry that relate to the shape and symmetry of the entire crystal.

Figure 11.6: The atomic arrangement in fluorite.

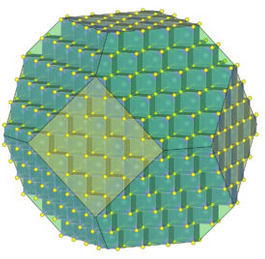
Figure 11.6 is the same figure we saw in Chapter 1. It shows the arrangement of atoms and building blocks in a fluorite crystal. Notice that the overall crystal has a sort of cube shape, and the building blocks are also cubes. This relationship between crystal symmetry and building block symmetry is at the heart of crystallography.

Early in the 1800s, several researchers found that crystals of similar, but not identical, chemical composition could have identical shapes. W. H. Wollaston (c. 1809) showed that calcite (CaCO₃), magnesite (MgCO₃), rhodochrosite (MnCO₃), and siderite (FeCO₃) all commonly formed the same distinctive rhombohedron-shaped crystals

Figure 11.7: Calcite

Figure 11.8: Magnesite from Minas Gerais, Brazil

Figure 11.9: Rhodochrosite from Colorado

Figure 11.10: Siderite from Mt. Saint Hilaire, Quebec

Those who studied sulfate compounds also found that crystals of different compositions had the same crystal shape. Both the rhombohedral carbonates and the sulfates are examples of isomorphous series. Wollaston and others concluded that when crystal shapes in such series are truly identical, the distribution of atoms within the crystals must be identical as well, even if the compositions are not. Minerals with identical atomic distributions are termed isostructural even if (unlike carbonates or sulfates) they have significantly different compositions.

Sometimes isostructural minerals form solid solutions because they can mix to form intermediate compositions. Fayalite (Fe₂SiO₄) and forsterite (Mg₂SiO₄) are isostructural and form a complete solid solution; olivines can have any composition between the two end members. In contrast, halite (NaCl) and periclase (MgO) are isostructural but do not form solid solutions. Calcite, magnesite, rhodochrosite, and siderite are isostructural but their mutual solubility is limited. They form only limited solid solutions, also called partial solid solutions.

In 1821 Eilhard Mitscherlich, a student of Berzelius’s, discovered that the same elements may combine in different atomic structures. For instance, calcite and aragonite both have composition CaCO₃, but they form different crystal shapes and have different physical properties. We call such minerals polymorphs because, although identical in composition, they have different atomic arrangements and crystal morphologies. Mineralogists have now studied several other CaCO₃ polymorphs, but none except vaterite occur naturally. In calcite and vaterite the basic building blocks have rhomb-shaped faces, while in aragonite the faces are rectangles.

Figure 11.11 shows calcite and siderite crystals that do not have the same shapes as those above in Figures 11.7 and 11.10. Many minerals, especially carbonate minerals have multiple common habits. Figure 11.12 shows aragonite crystals and Figure 11.13 shows vaterite crystals. Both minerals, like calcite, have composition CaCO₃.

Figure11.11: White calcite with siderite from the Pyrenees. The specimen is 11 cm tall.

Figure 11.12: Aragonite crystals from Guadalajara, Spain

Figure 11.13: White vaterite crystals from near Naples, Italy. The sample is 7.1 cm wide.

By the early/mid 1800s it was clear that there was no direct correlation between the shapes of building blocks and crystal composition, as Haüy had originally thought. Despite flaws in some of his ideas, however, we must credit René Haüy as one of the founders of crystallography. In later years, he pioneered the application of mathematical concepts to crystal properties which established the basis for modern crystallography and crystallographers still use much of his work today. We now accept that:

• All crystals have basic building blocks called unit cells.
• The unit cells are arranged in a pattern described by points in a lattice.
• The relative proportions of elements in a unit cell are given by the chemical formula of a mineral.
• Crystals belong to one of seven crystal systems. Unit cells of distinct shape and symmetry characterize each crystal system.
• Total crystal symmetry depends on both unit cell symmetry and lattice symmetry.