10.1.4: Rotational Symmetry

Figure 10.10: Rotational symmetry

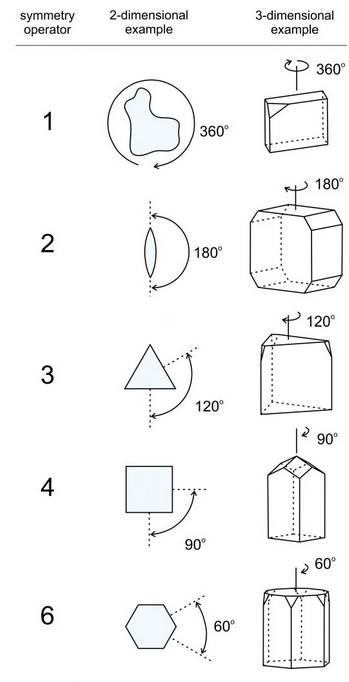
Reflection by a mirror is one of several types of symmetry operations. A second common type of symmetry in crystals, called rotational symmetry, is symmetry with respect to a line called a rotation axis. In two dimensions, a lens shape appears unchanged when rotated 180° (symmetry operator 2 in Figure 10.10). We say it has 2-fold symmetry because two repeats of a 180^o rotation operation return it to its original position. A 2-fold rotation axis is perpendicular to the plane of the page.

Figure 10.10 also shows other rotational symmetry operators. Equilateral triangles have 3-fold rotational symmetry. Rotate an equilateral triangle 120° and it appears the same. Do it three times and you are back to where you started.

Squares have 4-fold rotational symmetry (rotation of 90°), and hexagons have 6-fold rotational symmetry (rotation of 60°). Box 10-2 contains more examples of rotation axes in 2D.

The right-hand column in Figure 10.10 shows three-dimensional shapes – they might be crystals – with the different kinds of rotational symmetry (1-fold, 2-fold, 3-fold, 4-fold, and 6-fold). Many of them also contain mirror planes of symmetry. Thus we see that crystals may have more than one kind of symmetry. Fortunately the number of possible combinations is limited, which makes analyzing crystal symmetry easier than it would be otherwise.

All objects have 1-fold rotational symmetry because they remain unchanged after rotation of 360°. This seems trivial, but for completeness we have included 1-fold symmetry in Figure 10.10. And, although we can draw shapes that have 5-fold symmetry, or greater than 6-fold symmetry, minerals never possess such symmetry. For example, some natural materials, including plants and animals such as a starfish (having 5 legs), display apparent symmetries not possible for minerals. We will discuss why in the following chapter.

We call all the rotation axes we have just discussed proper rotation axes, to contrast them with rotoinversion axes, which we will discuss later. In shorthand notation, we symbolize proper rotation axes using the numbers 1, 2, 3, 4, or 6, corresponding to rotations of 360°, 180°, 120°, 90°, and 60°, respectively. The “fold” value tells us how many times the operation has to be repeated to return to the starting position – how many times it takes to add up to 360^o. Sometimes in drawings, we use a small lens shape, a triangle, a square, or a hexagon instead of numbers to show symmetry and label the different rotation axes.

Rotation Axes in 2D

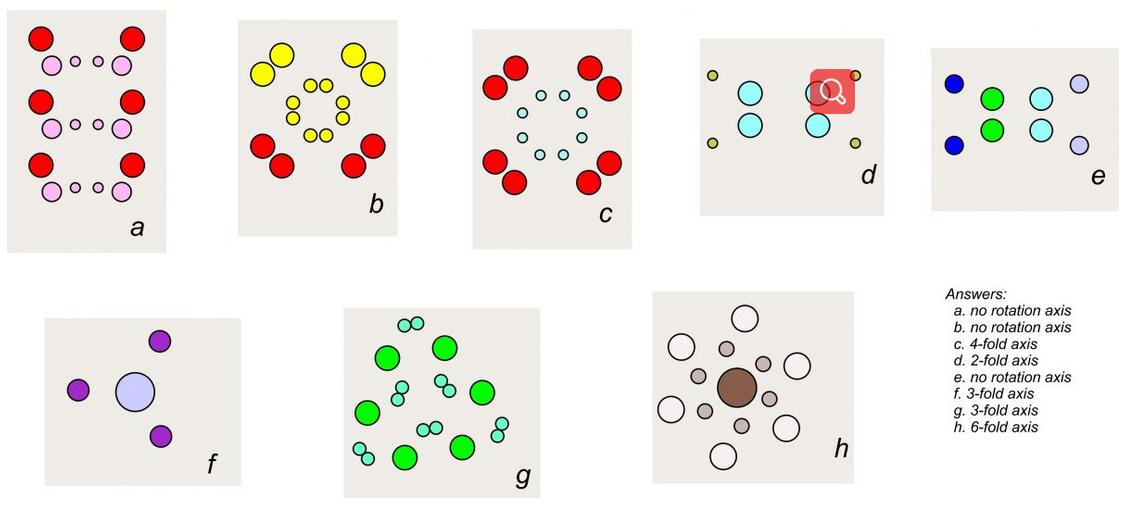
The drawings below show colorful patterns. Most are the same patterns you saw in the previous box. They all have 1-fold rotational symmetry. What other kinds of rotation axis (2-fold, 3-fold, 4-fold, or 6-fold) do you see in each drawing? (Some contain none.)

Figure 10.11: Some examples that may contain rotation axes

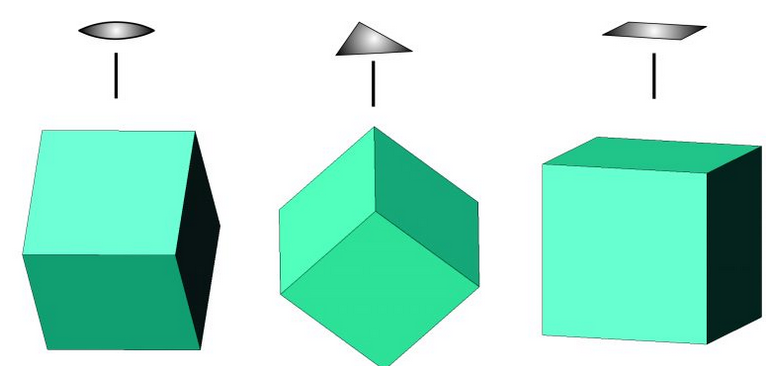
Above, we noted that cubes have nine mirror planes. Cubes also have 2-fold, 3-fold, and 4-fold rotational symmetry, shown in Figure 10.12. When rotated 180° about an edge diagonal, a cube appears unchanged drawing on left). When rotated 120° about a main diagonal (drawing in the center), or when rotated 90° about a line perpendicular to a face (drawing on the right), a cube does not change. Thus, we see that different rotation axes can combine in crystals. Cubes, with all their mirror planes and rotation axes, have the most symmetry possible for a crystal.

Figure 10.12: Rotational axes of a cube

Figure 10.13: Apophyllite on stilbite and calcite

Figure 10.14: Apatite crystal from Bahia State, Brazil. 7 cm tall

Many minerals grow as prisms, crystals having a set of identical faces parallel to one direction. Typically, prismatic crystals are elongated in one direction. Figure 10.13 shows a green prismatic crystal of apophyllite, a zeolite. The crystal has four vertical faces and a square cross section. It also has sloping terminating faces at the top and bottom ends. Figure 10.14 shows a hexagonal prism of apatite. The prism has six sides – all parallel to one direction – and terminating faces on its top. If the crystal was perfectly formed, there would also be six terminating faces on the bottom.

Prism faces are, in principle, identical in shape and size, although accidents of growth often lead to minor differences. Some minerals have multiple, nonidentically-shaped faces, all parallel to a common line. We call the collection of faces a zone and the common line the zone axis. Zones, present in most crystals, sometimes correspond to rotational axes of symmetry.

Symmetry can be enigmatic. For example, anhedral crystals exhibit no external symmetry, while euhedral crystals may exhibit a lot. And, rotational symmetry, even if present, may be hard to see. For example, the 3-fold axes of symmetry in a cube are difficult to see without turning the cube in your hand. Problems may be even more complicated in natural crystals because of growth imperfections in crystal faces, or the presence of many differently shaped crystal faces.