10.1.3: Mirror Planes

Last updated
Save as PDF

Page ID: 18467

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

10.7.jpg — Figure 10.7: Lions have symmetrical faces

Most animals, including humans and lions (Figure 10.7), appear symmetrical: an imaginary mirror down their center relates the appearance of their right side to their left side. We call such symmetry reflection, and we call the plane of the imaginary mirror the mirror plane. In shorthand notation, we use the letter m to designate a mirror of symmetry. Reflection is the symmetry operation, and the mirror plane is the symmetry operator. Reflection often relates identical faces on a crystal. Figure 10.8a shows a butterfly that has the same symmetry as a lion.

A face, or any object, on one side of a mirror has an equivalent at an equal distance on the other side of the mirror. The two faces or objects are the same perpendicular distance from the mirror and have opposite handedness, like your two hands shown in Figure 10.8b (one has the thumb on the left side and the other has the thumb on the right side).

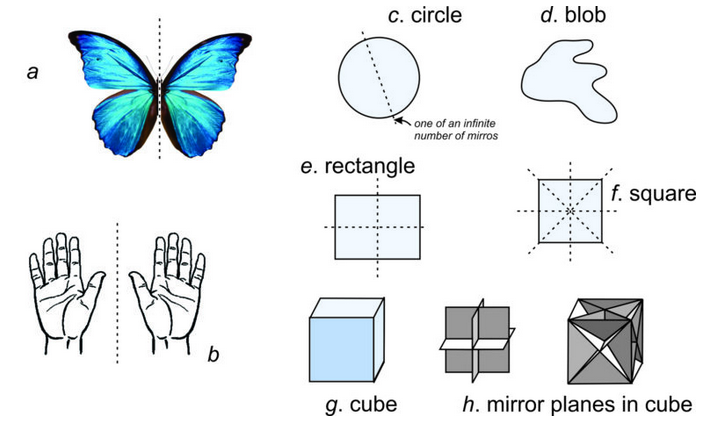
10.8.png — Figure 10.8: Mirror planes of symmetry

Two-dimensional drawings may have many mirror planes or no mirror planes. A circle (Figure 10.8c), for example, contains an infinite number of mirror planes; any line drawn through the center of the circle is a mirror of symmetry. Irregular blobs (Figure 10.8d), on the other hand, have no mirror planes. A rectangle (Figure 10.8e) contains two mirror planes, while squares (Figure 10.8f) have four. Box 10-1 contains more examples of mirror planes in 2D.

Three-dimensional objects, too, may have zero to many mirror planes. A cube (Figure 10.8g) has nine mirrors. Three are parallel to pairs of opposite faces; six intersect opposite faces along their diagonals (Figure 10.8h). Thus, a cube has more symmetry than a human, a lion, or a butterfly. (A perfect sphere has an infinite number of mirror planes, but, as we will see later, crystals cannot have more mirror planes than a cube.)

Mirror Planes in 2D

The drawings below show colorful patterns. Most of them contain mirror planes. How many mirror planes do you see in each pattern?

10.9.png — Figure 10.9: Some patterns that may contain mirror planes

For a video with further discussion of mirror planes:

Video 10-2: Mirror planes (6 minutes)