3.6: Density and Specific Gravity
- Page ID
- 17574
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
The Greek letter ρ (rho) symbolizes density. We usually give the density of a mineral in units of grams/cubic centimeter (gm/cm3). Density varies slightly depending on pressure or temperature, but most minerals have values between 2 and 8 gm/cm3. Borax, shown in this photo, has density of about 1.8 gm/cm3, lower than all other common minerals.
The polymorphs diamond and graphite are both made of carbon (C), but due to differences in atomic arrangements, diamond has density of 3.5 gm/cm3, while graphite’s is 2.2 gm/cm3. Graphite forms under Earth surface conditions, but diamond, with its high density, only forms deep in Earth where pressures are great. The Laws of Thermodynamics tell us that high pressures favor dense minerals, which makes sense because at high pressure things are squeezed together.
Accurate determination of density can be difficult or impossible because it requires knowing the volume of a crystal – which can be difficult to measure with accuracy. A related property, specific gravity (G), is often used instead. Specific gravity (unitless) is the ratio of the mass of a mineral to the mass of an equal volume of water at 1 atm, and because mass and weight are proportional, we normally determine specific gravity by comparing weights. If a mineral is at normal Earth surface conditions, density and specific gravity have about the same values.

Because specific gravity varies greatly between minerals, we can easily distinguish minerals with high, moderate, or low specific gravity simply by picking them up to see how heavy they feel. We use the term heft for estimations of G made using this approach. H is sometimes very useful for mineral identification. For example, the mineral barite (BaSO4), such as the example in Figure 3.74, sometimes exists as massive white material that is easily confused with feldspars. However, its great heft, easily discerned by picking it up, helps identify it. Similarly, we can distinguish cerussite (lead carbonate) from other carbonate minerals by its heft.
Specific gravity differences can also help in the separation of minerals. In the laboratory, researchers separate crushed rock into mineral components by “floating” samples in liquids of different specific gravities. In these heavy liquids, which are much denser than water, minerals separate as some float and others sink according to their specific gravities. In mining operations, ore minerals are often separated from valueless minerals by using gravity separation techniques that depend on specific gravity differences. This occurs in natural systems, too. Placer gold deposits form when gold from weathered rock, because of its high specific gravity, concentrates in stream beds.

The lightest minerals have specific gravities on the order of 1.8 to 2. They are mostly borates (such as borax), halides (e.g., halite), and sulfates (e.g., gypsum). Silicates (including quartz and all the other common rock-forming silicates) and carbonates (e.g., calcite or dolomite) range from about 2.5 to 3.5. Oxides and sulfides may have specific gravities as great as 7 or 8 but are highly variable. And, native metals (e.g., copper, silver, or gold) range up to 19 or 20. The photo in Figure 3.75 shows a gold nugget with quartz beneath it. It came from a placer. Gold has specific gravity of about 19.3 and quartz has specific gravity of 2.7.
The specific gravity of a mineral depends, in part, on how its atoms are packed together within a crystal. For example, the left part of the table below lists the specific gravities for quartz and four other SiO2 polymorphs. Stishovite, coesite, quartz, cristobalite, and tridymite all have different densities because they do not have the same atomic arrangements. The densest two – stishovite and coesite – are only found in very high pressure rocks or in meteorite impact craters.
Specific gravity also depends on composition. This can be demonstrated by looking at isostructural minerals – minerals with the same atomic arrangement but with different compositions. Consider the garnet group minerals for example. The table below lists names, compositions and specific gravities for seven garnets. The specific gravity values vary from 3.54 for pyrope to 4.33 for almandine, reflecting the atomic weights of the garnets’ elemental constituents. Two examples of garnet can be seen in Figures 3.6 and 3.7.
| Specific Gravities of Some Silica Polymorphs | ||
| mineral | formula | G |
| stishovite | SiO2 | 4.35 |
| coesite | SiO2 | 3.01 |
| quartz | SiO2 | 2.65 |
| cristobalite | SiO2 | 2.32 |
| tridymite | SiO2 | 2.26 |
| Specific Gravities of Some Garnet Minerals | ||
| mineral | formula | G |
| pyrope | Mg3Al2Si3O12 | 3.54 |
| grossular | Ca3Al2Si3O12 | 3.56 |
| uvarovite | Ca3Cr2Si3O12 | 3.80 |
| andradite | Ca3Fe2Si3O12 | 3.86 |
| spessartine | Mn3Al2Si3O12 | 4.19 |
| almandine | Fe3Al2Si3O12 | 4.33 |
Graphite and Diamond

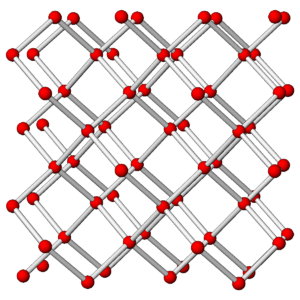
The photos in Figures 3.76 and 3.78 show a diamond crystal and a graphite crystal. Graphite and diamond are polymorphs – they have the same compositions but different atomic arrangements.
Both minerals are made of carbon but they have different properties and appearances because the carbon atoms are arranged differently in the two minerals. The drawings in Figures 3.77 and 3.79 show how carbon atoms are arranged in each.
As shown in the atomic drawings, in diamond, each carbon atom is covalently bonded to four others, creating an overall cubic 3-dimensional network that has the same properties in all directions. In graphite, carbon atoms are covalently bonded to form sheets that contain interconnected 6-carbon rings; very weak van der Waals bonds hold the sheets together.

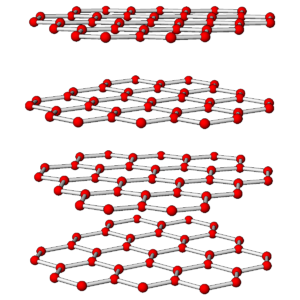
Diamond is a tenacious mineral that does not cleave easily. In contrast, graphite, because of its layered atomic arrangement, has excellent basal (planar) cleavage. Graphite has a hardness of 1½ and diamond has a hardness of 10. In diamond, all electrons are tied up in covalent bonds, so diamond does not conduct electricity. In graphite, there is a free electron associated with each carbon atom, so graphite conducts electricity well. Diamond has a denser structure than graphite – the specific gravity of diamond is about 3.5, and graphite’s is 2.1 to 2.3. Because of its high density, diamond only forms deep within Earth. This is true for all high density minerals – they only form where pressure is great.


