2.5: Compositional Variation in Minerals

2.19 Cleavelandite (albite-rich plagioclase)

Most natural minerals are formed from combinations of many elements. Unlike mechanical mixtures (such as two things being ground up together) the elements are ordered and intimately bonded together. The resulting crystalline solutions are solid solutions. Common plagioclase (a feldspar), for example, is mostly a solution of CaAl₂Si₂O₈ (anorthite) and NaAlSi₃O₈ (albite). It may also contain a small amount of orthoclase (KAlSi₃O₈). Anorthite, albite, and orthoclase are plagioclase end-members. End-member formulas describe ideal components that make up solid-solution minerals. The plagioclase sample seen in Figure 2.19 contains blades of a variety of plagioclase called cleavelandite accompanied by a few small flakes of silver-gray muscovite. Cleavelandite has composition close to end-member albite.

Some minerals, such as hornblende, contain many elements, and are complex solid solutions that have long and complicated formulas. Other minerals, including plagioclase and other feldspars, have limited compositional variations. Still others, such as fluorite (CaF₂) or quartz (SiO₂), have relatively simple formulas and vary little from their ideal compositions.

We may broadly classify the elements that comprise a mineral in one of three categories: major elements, minor elements, and trace elements. Major elements are those fundamental to a mineral; they control a mineral’s basic atomic structure and gross properties. They must be in the mineral or the mineral has been misidentified. Minor elements are those present in small amounts, usually as replacements for a major element. Such elements, perhaps in amounts up to a several weight %, may affect color and a few other properties, but the basic atomic arrangement of a mineral is controlled by its major element chemistry. Minerals also contain extremely small amounts of elements called trace elements. Trace elements are in all minerals and provide valuable information for geologists attempting to determine how, when, and where specific minerals formed. They have little effect on most mineral properties. A notable exception to this is sometimes color; even trace amounts of some elements can have major effects on a mineral’s color.

Mineralogists can acquire mineral analyses in many ways. In the past, most chemical analyses were determined by titration and other “wet chemical” techniques. Today we use sophisticated analytical instruments, including atomic absorption spectrophotometers and electron microprobes. We normally report analytical results by listing oxide weight percentages. We must convert weight percent values to mole value if we wish to have mineral formulas.

2.20 Crystals of olivine

As an example of chemical variability in minerals, let’s consider olivine. An example of olivine is shown in Figure 2.20, above, and the table below lists analyses of six olivines from different geologic environments. The top part of the table presents the analyses in terms of element weight %; the middle part presents the same information in terms of oxide weight %; the bottom part presents the composition in terms of the number of atoms in an olivine formula. The three parts of the table are redundant; values from one can be converted to the others by an arithmetical process called normalization (described later in this chapter). Most mineralogists and petrologists prefer to consider oxide weight % (for reasons explained in a later chapter), or numbers of atoms (because numbers of atoms directly translate into mineral formulas), instead of element weight %.

Olivine Analysis
Source:	Burma	Finland	NewX Zealand	Minnesota	EastXX Greenland	Germany
Element Weight %
Si Ti Al Fe Mn Mg Ca Na O Total	19.50 0.00 0.00 0.86 0.00 34.88 0.00 0.00 45.43 100.67	19.21 0.03 0.29 3.39 0.18 32.60 0.00 0.00 45.20 100.90	19.15 0.01 0.11 6.11 0.10 31.27 0.11 0.01 44.56 101.43	14.22 0.72 0.26 44.79 0.00 4.93 0.94 0.00 33.86 99.72	14.09 0.12 0.04 50.84 0.78 0.63 1.56 0.00 32.06 100.12	13.94 0.00 0.00 54.01 0.22 0.00 0.00 0.00 31.41 99.58
Oxide Weight %
SiO2 TiO2 Al2O3 FeO MnO MgO CaO Na2O Total	41.72 0.00 0.00 1.11 0.00 57.84 0.00 0.00 100.67	41.10 0.05 1.10 4.36 0.23 54.06 0.00 0.00 100.90	40.97 0.02 0.42 7.86 0.13 51.85 0.15 0.03 101.43	30.42 1.20 0.98 57.62 0.00 8.18 1.32 0.00 99.72	30.14 0.20 0.15 65.40 1.01 1.04 2.18 0.00 100.12	29.82 0.00 0.00 69.48 0.28 0.00 0.00 0.00 99.58
Atoms per 4 Oxygen
Si Ti Al Fe Mn Mg Ca Na Total	0.978 0.000 0.000 0.022 0.000 2.022 0.000 0.000 3.022	0.968 0.001 0.015 0.086 0.005 1.899 0.000 0.000 2.974	0.979 0.000 0.006 0.157 0.003 1.848 0.004 0.001 2.998	0.957 0.028 0.018 1.516 0.000 0.383 0.044 0.000 2.946	1.001 0.005 0.003 1.817 0.028 0.052 0.078 0.000 2.984	1.011 0.000 0.000 1.970 0.008 0.000 0.000 0.000 2.989

As the analyses above show, Mg, Fe, and Si are major elements in olivines. Olivine may also contain Ca, Mn, Ti, and sometimes Ni or Cr, but except in extremely rare circumstances, these elements are minor or trace elements.

The compositions of these six olivines are all different. Silicon, magnesium, and iron are especially variable. How can we make better sense of it all? The answer is to use the atom numbers in the bottom third of the table above to write formulas for each olivine. The ideal stoichiometry (ratios of elements) of olivine is (R)₂SiO₄, where R is usually Fe, Mg, Mn, or Ca. Thus, a general formula is (Fe,Mg,Mn,Ca)₂SiO₄ and a good olivine analysis should produce a formula close to this. Formulas for each of the six olivines – seen in the table below – come out to be very close to ideal. Apparent deviations from ideal stoichiometry (for example, the numbers of Si in the formulas are not exactly equal to 1) can mostly be attributed to inclusions of other minerals within the olivine, or to analytical error.

Normalized Olivine Formulas
specimen source	formula	% forsterite Mg2SiO4	% fayalite Fe2SiO4
Burma Finland New Zealand Minnesota East Greenland Germany	(Mg2.022Fe0.022)Si0.978O4 (Mg1.899Fe0.086Mn0.005Al0.015Ti0.001)Si0.968O4 (Mg1.848Fe0.157Mn0.003Ca0.004Al0.006)Si0.979O4 (Mg0.383Fe1.516Ca0.044Al0.018Ti0.028)Si0.957O4 (Mg0.052Fe1.817Mn0.028Ca0.078Al0.003Ti0.005)Si1.001O4 (Fe1.970Mn0.008)Si1.011O4	98.94xx 95.67xx 92.16xx 20.19xx 2.77xx 0.00xx	1.06xx 4.33xx 7.84xx 79.81xx 97.23xx 100.00xx

Chemical substitutions in some minerals involve many elements and are complex. In olivine the substitutions are relatively simple. We can describe the compositions of most natural olivines as combinations of the end members (represented by ideal formulas) called forsterite (Mg₂SiO₄), fayalite (Fe₂SiO₄), tephroite (Mn₂SiO₄), and calcio-olivine (Ca₂SiO₄). In contrast with olivine, many minerals (for example amphiboles and micas) have lengthy formulas and have many elements substituting in their structures. For such minerals, choosing useful end members is difficult and arbitrary.

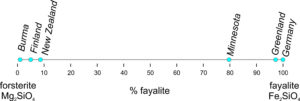
2.21 Comparing olivine compositions

The six olivines considered above contain very little besides forsterite and fayalite. This is typical for most olivines and, if we ignore the other components, we get the percent values in the two columns on the right in the table. The % forsterite and % fayalite were calculated, respectively, from the ratio of Mg/(Mg+Fe) and the ratio of Fe/(Mg+Fe) in each olivine. The binary (2-component) diagram below (Figure 2.21) shows the compositions plotted on a line anchored by pure forsterite on the left, and pure fayalite on the right. The sample from Burma is nearly 100% forsterite (Mg₂SiO₄), while that from Germany is 100% fayalite (Fe₂SiO₄). The other olivines fall between.

The degree to which elements may substitute for each other depends on the elements and on the mineral. In olivine, Fe and Mg mix freely, so any composition between fayalite and forsterite is possible. Olivines can incorporate only minor amounts of Ca, however, so no compositions midway between calcio-olivine and forsterite are found in nature. In contrast, Ca, Mg, and Fe mix freely in some other minerals, garnets for example. Natural garnets can have any composition between end members grossular (Ca₃Al₂Si₃O₁₂), almandine (Fe₃Al₂Si₃O₁₂), and pyrope (Mg₃Al₂Si₃O₁₂).