7.2: Absolute Dating
- Page ID
- 6882
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Relative time allows scientists to tell the story of Earth events, but does not provide specific numeric ages, and thus, the rate at which geologic processes operate. Based on Hutton’s principle of uniformitarianism (see Chapter 1), early geologists surmised geological processes work slowly and the Earth is very old. Relative dating principles was how scientists interpreted Earth history until the end of the 19th Century. Because science advances as technology advances, the discovery of radioactivity in the late 1800s provided scientists with a new scientific tool called radioisotopic dating. Using this new technology, they could assign specific time units, in this case years, to mineral grains within a rock. These numerical values are not dependent on comparisons with other rocks such as with relative dating, so this dating method is called absolute dating [5]. There are several types of absolute dating discussed in this section but radioisotopic dating is the most common and therefore is the focus on this section.
Radioactive Decay

All elements on the Periodic Table of Elements (see Chapter 3) contain isotopes. An isotope is an atom of an element with a different number of neutrons. For example, hydrogen (H) always has 1 proton in its nucleus (the atomic number), but the number of neutrons can vary among the isotopes (0, 1, 2). Recall that the number of neutrons added to the atomic number gives the atomic mass. When hydrogen has 1 proton and 0 neutrons it is sometimes called protium (1H), when hydrogen has 1 proton and 1 neutron it is called deuterium (2H), and when hydrogen has 1 proton and 2 neutrons it is called tritium (3H).
Many elements have both stable and unstable isotopes. For the hydrogen example, 1H and 2H are stable, but 3H is unstable. Unstable isotopes, called radioactive isotopes, spontaneously decay over time releasing subatomic particles or energy in a process called radioactive decay. When this occurs, an unstable isotope becomes a more stable isotope of another element. For example, carbon-14 (14C) decays to nitrogen-14 (14N).

The radioactive decay of any individual atom is a completely unpredictable and random event. However, some rock specimens have an enormous number of radioactive isotopes, perhaps trillions of atoms and this large group of radioactive isotopes do have a predictable pattern of radioactive decay. The radioactive decay of half of the radioactive isotopes in this group takes a specific amount of time. The time it takes for half of the atoms in a substance to decay is called the half-life. In other words, the half-life of an isotope is the amount of time it takes for half of a group of unstable isotopes to decay to a stable isotope. The half-life is constant and measurable for a given radioactive isotope, so it can be used to calculate the age of a rock. For example, the half-life uranium-238 (238U) is 4.5 billion years and the half-life of 14C is 5,730 years.
The principles behind this dating method require two key assumptions. First, the mineral grains containing the isotope formed at the same time as the rock, such as minerals in an igneous rock that crystallized from magma. Second, the mineral crystals remain a closed system, meaning they are not subsequently altered by elements moving in or out of them.

These requirements place some constraints on the kinds of rock suitable for dating, with the igneous rock being the best. Metamorphic rocks are crystalline, but the processes of metamorphism may reset the clock and derived ages may represent a smear of different metamorphic events rather than the age of original crystallization. Detrital sedimentary rocks contain clasts from separate parent rocks from unknown locations and derived ages are thus meaningless. However, sedimentary rocks with precipitated minerals, such as evaporites, may contain elements suitable for radioisotopic dating. Igneous pyroclastic layers and lava flows within a sedimentary sequence can be used to date the sequence. Cross-cutting igneous rocks and sills can be used to bracket the ages of affected, older sedimentary rocks. The resistant mineral zircon, found as clasts in many ancient sedimentary rocks, has been successfully used for establishing very old dates, including the age of Earth’s oldest known rocks [6] Knowing that zircon minerals in metamorphosed sediments came from older rocks that are no longer available for study, scientists can date zircon to establish the age of the pre-metamorphic source rocks.

There are several ways radioactive atoms decay. We will consider three of them here—alpha decay, beta decay, and electron capture. Alpha decay is when an alpha particle, which consists of two protons and two neutrons, is emitted from the nucleus of an atom. This also happens to be the nucleus of a helium atom; helium gas may get trapped in the crystal lattice of a mineral in which alpha decay has taken place. When an atom loses two protons from its nucleus, lowering its atomic number, it is transformed into an element that is two atomic numbers lower on the Periodic Table of the Elements.
CC BY-SA 4.0], via Wikimedia Commons" width="778px" height="415px" src="/@api/deki/files/7554/07.11_periodic_table-300x160.png">
Periodic Table of the Elements
The loss of four particles, in this case, two neutrons and two protons, also lowers the mass of the atom by four. For example, alpha decay takes place in the unstable isotope 238U, which has an atomic number of 92 (92 protons) and a mass number of 238 (total of all protons and neutrons). When 238U spontaneously emits an alpha particle, it becomes thorium-234 (234Th). The radioactive decay product of an element is called its daughter isotope and the original element is called the parent isotope. In this case, 238U is the parent isotope and 234Th is the daughter isotope. The half-life of 238U is 4.5 billion years, i.e., the time it takes for half of the parent isotope atoms to decay into the daughter isotope. This isotope of uranium, 238U, can be used for absolute dating the oldest materials found on Earth, and even meteorites and materials from the earliest events in our solar system.

Beta Decay is when a neutron in its nucleus splits into an electron and a proton. The electron is emitted from the nucleus as a beta ray. The new proton increases the element’s atomic number by one, forming a new element with the same atomic mass as the parent isotope. For example, 234Th is unstable and undergoes beta decay to form protactinium-234 (234Pa), which also undergoes beta decay to form uranium-234 (234U). Notice these are all isotopes of different elements but they have the same atomic mass of 234. The decay process of radioactive elements like uranium keeps producing radioactive parents and daughters until a stable, or non-radioactive, daughter is formed. Such a series is called a decay chain. The decay chain of the radioactive parent isotope 238U progresses through a series of alpha (red arrows on the adjacent figure) and beta decays (blue arrows) until it forms the stable daughter isotope, lead-206 (206Pb).
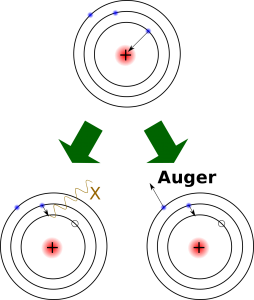
Electron capture is when a proton in the nucleus captures an electron from one of the electron shells and becomes a neutron. This produces one of two different effects: 1) an electron jumps in to fill the missing spot of the departed electron and emits an X-ray, or 2) in what is called the Auger process, another electron is released and changes the atom into an ion. The atomic number is reduced by one and the mass number remains the same. An example of an element that decays by electron capture is potassium-40 (40K). Radioactive 40K makes up a tiny percentage (0.012%) of naturally occurring potassium, most of which not radioactive. 40K decays to argon-40 (40Ar) with a half-life of 1.25 billion years, so it is very useful for dating geological events [7]. Below is a table of some of the more commonly-used radioactive dating isotopes and their half-lives.
| Elements | Parent symbol | Daughter symbol | Half-life |
| Uranium-238/Lead-206 | 238U | 206Pb | 4.5 billion years |
| Uranium-235/Lead-207 | 235U | 207Pb | 704 million years |
| Potassium-40/Argon-40 | 40K | 40Ar | 1.25 billion years |
| Rubidium-87/Strontium-87 | 87Rb | 87Sr | 48.8 billion years |
| Carbon-14/Nitrogen-14 | 14C | 14N | 5,730 years |
Radioisotopic Dating

For a given sample of rock, how is the dating procedure carried out? The parent and daughter isotopes are separated out of the mineral using chemical extraction. In the case of uranium, 238U and 235U isotopes are separated out together, as are the 206Pb and 207Pb with an instrument called a mass spectrometer [9].
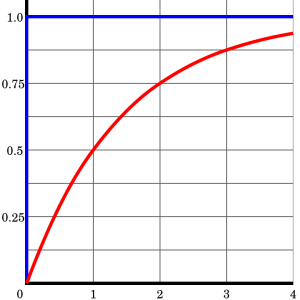
Here is a simple example of age calculation using the daughter-to-parent ratio of isotopes. When the mineral initially forms, it consists of 0% daughter and 100% parent isotope, so the daughter-to-parent ratio (D/P) is 0. After one half-life, half the parent has decayed so there is 50% daughter and 50% parent, a 50/50 ratio, with D/P = 1. After two half-lives, there is 75% daughter and 25% parent (75/25 ratio) and D/P = 3. This can be further calculated for a series of half-lives as shown in the table. The table does not show more than 10 half-lives because, after about 10 half-lives, the amount of remaining parent is so small it becomes too difficult to accurately measure via chemical analysis. Modern applications of this method have achieved remarkable accuracies of plus or minus two million years in 2.5 billion years (that’s ±0.055%) [10]. Applying the uranium/lead technique in any given sample analysis provides two separate clocks running at the same time, 238U and 235U. The existence of these two clocks in the same sample gives a cross-check between the two. Many geological samples contain multiple parent/daughter pairs, so cross-checking the clocks confirms that radioisotopic dating is highly reliable.
| Half-lives (#) | Parent present (%) | Daughter present (%) | Daughter/ Parent ratio | Parent/ Daughter ratio |
| Start the clock | 100 | 0 | 0 | infinite |
| 1 | 50 | 50 | 1 | 1 |
| 2 | 25 | 75 | 3 | 0.33 |
| 3 | 12.5 | 87.5 | 7 | 0.143 |
| 4 | 6.25 | 93.75 | 15 | 0.0667 |
| 5 | 3.125 | 96.875 | 31 | 0.0325 |
| 10 | 0.098 | 99.9 | 1023 | 0.00098 |
The ratio of parent to a daughter in terms of half-life.
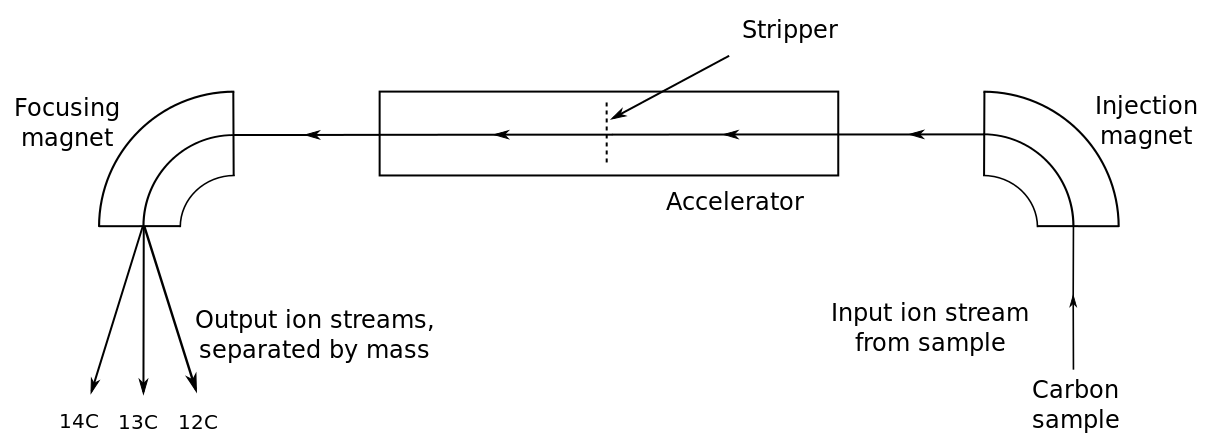
Another radioisotopic dating method involves carbon and is useful for dating archaeologically important samples containing organic substances like wood or bone. Radiocarbon dating, also called carbon dating, uses the unstable isotope carbon-14 (14C) and the stable isotope carbon-12 (12C). Carbon-14 is constantly being created in the atmosphere by the interaction of cosmic particles with atmospheric nitrogen-14 (14N) [11]. Cosmic particles such as neutrons strike the nitrogen nucleus, kicking out a proton but leaving the neutron in the nucleus. The collision reduces the atomic number by one, changing it from seven to six, changing the nitrogen into carbon with the same mass number of 14. The 14C quickly bonds with oxygen (O) in the atmosphere to form carbon dioxide (14CO2) that mixes with another atmospheric carbon dioxide (12CO2) while this mix of gases is incorporated into living matter. While an organism is alive, the ratio of 14C/12C in its body doesn’t really change since CO2 is constantly exchanged with the atmosphere. However, when it dies, the radiocarbon clock starts ticking as the 14C decays back to 14N by beta decay, which has a half-life of 5,730 years. The radiocarbon dating technique is thus useful for 57,300 years or so, about 10 half-lives back.
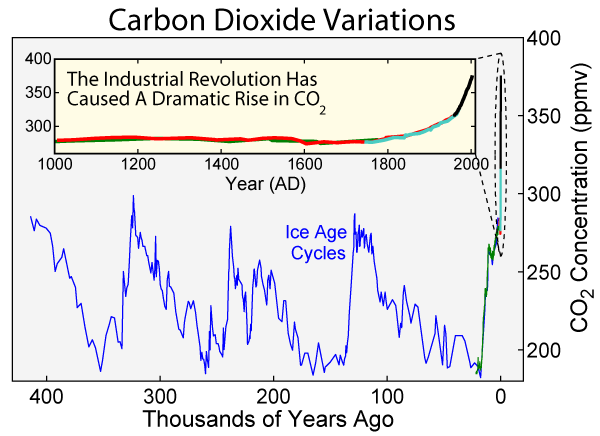
Radiocarbon dating relies on daughter-to-parent ratios derived from a known quantity of parent 14C. Early applications of carbon dating assumed the production and concentration of 14C in the atmosphere remained fairly constant for the last 50,000 years. However, it is now known that the amount of parent 14C levels in the atmosphere. Comparisons of carbon ages with tree-ring data and other data for known events have allowed reliable calibration of the radiocarbon dating method. Taking into account carbon-14 baseline levels must be calibrated against other reliable dating methods, carbon dating has been shown to be a reliable method for dating archaeological specimens and very recent geologic events.
Age of the Earth

The work of Hutton and other scientists gained attention after the Renaissance (see Chapter 1), spurring exploration into the idea of an ancient Earth. In the late 19th century William Thompson, a.k.a. Lord Kelvin, applied his knowledge of physics to develop the assumption that the Earth started as a hot molten sphere. He estimated the Earth is 98 million years old, but because of uncertainties in his calculations stated the age as a range of between 20 and 400 million years [12; 13]. This animation (also shown below) illustrates how Kelvin calculated this range and why his numbers were so far off, which has to do with unequal heat transfer within the Earth. It has also been pointed out that Kelvin failed to consider pliability and convection in the Earth’s mantle as a heat transfer mechanism. Kelvin’s estimate for Earth’s age was considered plausible but not without challenge, and the discovery of radioactivity provided a more accurate method for determining ancient ages [14].
In the 1950s, Clair Patterson (1922–1995) thought he could determine the age of the Earth using radioactive isotopes from meteorites, which he considered to be early solar system remnants that were present at the time Earth was forming. Patterson analyzed meteorite samples for uranium and lead using a mass spectrometer. He used the uranium/lead dating technique in determining the age of the Earth to be 4.55 billion years, give or take about 70 million (± 1.5%) [15]. The current estimate for the age of the Earth is 4.54 billion years, give or take 50 million (± 1.1%) [13]. It is remarkable that Patterson, who was still a graduate student at the University of Chicago, came up with a result that has been little altered in over 60 years, even as technology has improved dating methods.
Dating Geological Events

Radioactive isotopes of elements that are common in mineral crystals are useful for radioisotopic dating. The uranium/lead method, with its two cross-checking clocks, is most often used with crystals of the mineral zircon (ZrSiO4) where uranium can substitute for zirconium in the crystal lattice. Zircon is resistant to weathering which makes it useful for dating geological events in ancient rocks. During metamorphic events, zircon crystals may form multiple crystal layers, with each layer recording the isotopic age of an event, thus tracing the progress of the several metamorphic events [16].
Geologists have used zircon grains to do some amazing studies that illustrate how scientific conclusions can change with technological advancements. Zircon crystals from Western Australia that formed when the crust first differentiated from the mantle 4.4 billion years ago have been determined to be the oldest known rocks [6]. The zircon grains were incorporated into metasedimentary host rocks, sedimentary rocks showing signs of having undergone partial metamorphism. The host rocks were not very old but the embedded zircon grains were created 4.4 billion years ago and survived the subsequent processes of weathering, erosion, deposition, and metamorphism. From other properties of the zircon crystals, researchers concluded that not only were continental rocks exposed above sea level but also that conditions on the early Earth were cool enough for liquid water to exist on the surface. The presence of liquid water allowed the processes of weathering and erosion to take place [17]. Researchers at UCLA studied 4.1 billion-year-old zircon crystals and found carbon in the zircon crystals that may be biogenic in origin, meaning that life may have existed on Earth much earlier than previously thought [18].

Igneous rocks best suited for radioisotopic dating because their primary minerals provide dates of crystallization from magma. Metamorphic processes tend to reset the clocks and smear the igneous rock’s original date. Detrital sedimentary rocks are less useful because they are made of minerals derived from multiple parent sources with potentially many dates. However, scientists can use igneous events to date sedimentary sequences. For example, if sedimentary strata are between a lava flow and volcanic ash bed with radioisotopic dates of 54 million years and 50 million years, then geologists know the sedimentary strata and its fossils formed between 54 and 50 million years ago. Another example would be a 65 million-year-old volcanic dike that cut across sedimentary strata. This provides an upper limit age on the sedimentary strata, so these strata would be older than 65 million years. Potassium is common in evaporite sediments and has been used for potassium/argon dating [19]. Primary sedimentary minerals containing radioactive isotopes like 40K has provided dates for important geologic events.
Other Absolute Dating Techniques

Luminescence (aka Thermoluminescence): Radioisotopic dating is not the only way scientists determine numeric ages. Luminescence dating measures the time elapsed since some silicate minerals, such as coarse-sediments of silicate minerals, were last exposed to light or heat at the surface of Earth. All buried sediments are exposed to radiation from normal background radiation from the decay process described above. Some of these electrons get trapped in the crystal lattice of silicate minerals like quartz. When exposed at the surface, ultraviolet radiation and heat from the Sun release these electrons, but when the minerals are buried just a few inches below the surface, the electrons get trapped again. Samples of coarse sediments collected just a few feet below the surface are analyzed by stimulating them with light in a lab. This stimulation releases the trapped electrons as a photon of light which is called luminescence. The amount luminescence released indicates how long the sediment has been buried. Luminescence dating is only useful for dating sediments young sediment that is less than 1 million years old [20; 21]. In Utah, luminescence dating is used to determine when coarse-grained sediment layers were buried near a fault. This is one technique used to determine the recurrence interval of large earthquakes on faults like the Wasatch Fault that primarily cut coarse-grained material and lack buried organic soils for radiocarbon dating [22].

Fission Track: Fission track dating relies on damage to the crystal lattice produced when unstable 238U decays to the daughter product 234Th and releases an alpha particle. These two decay products move in opposite directions from each other through the crystal lattice leaving a visible track of damage. This is common in uranium-bearing mineral grains such as apatite. The tracks are large and can be visually counted under an optical microscope. The number of tracks corresponds to the age of the grains. Fission track dating works from about 100,000 to 2 billion (1 × 105 to 2 × 109) years ago. Fission track dating has also been used as a second clock to confirm dates obtained by other methods [23; 7].
References
7. Dickin, A. P. Radiogenic isotope geology. (Cambridge University Press, 2005).
11. Burleigh, R. W. F. Libby and the development of radiocarbon dating. Antiquity 55, 96–98 (1981).
12. MacDougall, Doug. Nature’s clocks: how scientists measure the age of almost everything. (2008).
13. Brent Dalrymple, G. The Age of the Earth. (Stanford University Press, 1994).
15. Patterson, C. Age of meteorites and the earth. Geochim. Cosmochim. Acta 10, 230–237 (1956).
16. Ireland, T. New tools for isotopic analysis. Science 286, 2289–2290 (1999).


