12.2: Assignment- Calculating and Assessing Flood Recurrence Intervals
- Page ID
- 6103
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Module 12 Assignment
Exploring Earth’s layers and seismic-wave travel times

Overview
Flooding is a common and serious problem in our nation’s waterways. Flood stage is reached when the water level in a stream overflows its banks. Floodplains are popular sites for development, with nice water views, but are best left for playgrounds, golf courses, and the like. Have you ever heard someone say that a flood was a 1 in 100 year flood? Does that mean that a flood of similar magnitude will occur every 100 years? No, it only means that, on average, we can expect a flood of this size or greater to occur within a 100 year period. One cannot predict that it will occur in a particular year, only that each year has a 1 in 100 chance of having a flood of that magnitude. It also does not mean that only 1 flood of that size can occur within 100 years.
In order to better understand stream behavior, the U.S. Geological Survey has installed thousands of stream gauges throughout the country, locations with a permanent water level indicator and recorder. Data from these stations can be used to make flood frequency curves, which are useful in making flood control decisions. In western Georgia, a dramatic flood event occurred in September, 2009 that resulted in 11 fatalities, over $200 million in property damage, and closed Interstate 20 for a day. Rain fell from September 16-22, with a particularly intense period on September 20th. Use information below from a stream gauge located on Sweetwater Creek near Austell, Georgia, to create a flood frequency graph.
Instructions
Data from the chart below was collected from a USGS stream gage, and includes the 20 largest discharge events for Sweetwater Creek at station 02337000 from January 1, 2008 – May 1, 2015, excluding the dramatic 2009 flood. In order to create a flood frequency graph, first the recurrence interval must be calculated (one is calculated below for an example). A recurrence interval refers to the average time period within which a given flood event will be equaled or exceeded once. To calculate it, first determine the rank of the flood, with a 1 going to the highest discharge event and a 20 going to the lowest discharge event. Calculate the recurrence interval using the following equation:
\[RI = (n+1) / m\]
where
- RI = Recurrence Interval (yrs)
- n = number of years of record (in this case, 2008 – 2015 = 8 individual years of record)
- m = rank of flood
Therefore, within this particular record of data, the recurrence interval for each flood would be calculated as:
\[RI = 9 / m\]
| Peak Discharge Date | Discharge (cfs – cubic feet per second) | Rank (1-20) | Recurrence Intervals |
|---|---|---|---|
| 87/27/2008 | 5,140 | ||
| 3/2/2009 | 2,360 | ||
| 10/13/2009 | 3,290 | ||
| 11/12/2009 | 6,120 | 1 | 9 |
| 12/3/2009 | 2,860 | ||
| 12/10/2009 | 2,170 | ||
| 12/19/2009 | 3,830 | ||
| 12/26/2009 | 2,650 | ||
| 1/25/2010 | 2,500 | ||
| 2/6/2010 | 3,680 | ||
| 3/12/2010 | 2,350 | ||
| 4/17/2011 | 3,100 | ||
| 2/24/2013 | 2,060 | ||
| 2/27/2013 | 2,190 | ||
| 5/6/2013 | 3,610 | ||
| 12/23/2013 | 3,790 | ||
| 4/8/2014 | 4,170 | ||
| 1/5/2015 | 3,970 | ||
| 4/20/2015 | 2,940 |
Flood Recurrence Intervals as Probabilities
Your results for recurrence interval will tell you the probability that a flood of a particular magnitude will occur in any given year. If you roll a single dice, the chance of rolling a 4 will be a 1-in-6 chance, because there are only 6 possible outcomes on the dice. You could roll the dice a second time, and your chances of it landing on a 4 are still the same (1 in 6). You can think about flood recurrence intervals in the same way. If you calculate a recurrence interval of 3 for a flood event with a discharge of 3,000 cfs, it means that particular flood has a 1-in-3 chance of occurring in any given year. Another way of thinking about it is to say that a flood event with a discharge of 3,000 cfs is a “3-year flood.” It does not mean, however, that a flood of this magnitude will only occur every 3 years. In fact, two or more 3-year floods could easily occur within weeks or months of each other, or the opposite could be true, where there could easily be 10 years or more between two floods of this magnitude. In the same way, if you roll a dice, it could land on a 4 twice in a row, even though it is still a 1-in-6 probability each time you roll the dice. The recurrence interval simply represents the chance that something will occur.
Graphing Your Results and Drawing Best-Fit Line
You will be graphing these data and drawing a “best fit line” through the points in order to calculate the slope of line and examine trends in the data. An example of this process is shown below using data of sea-ice extent from the assignment in the Climate Change module. Use a straight edge to draw a best-fit line (a straight line along the graph that shows the general direction that the group of points seem to be heading – it doesn’t have to hit every point on the graph) through the data after all the points have been plotted.
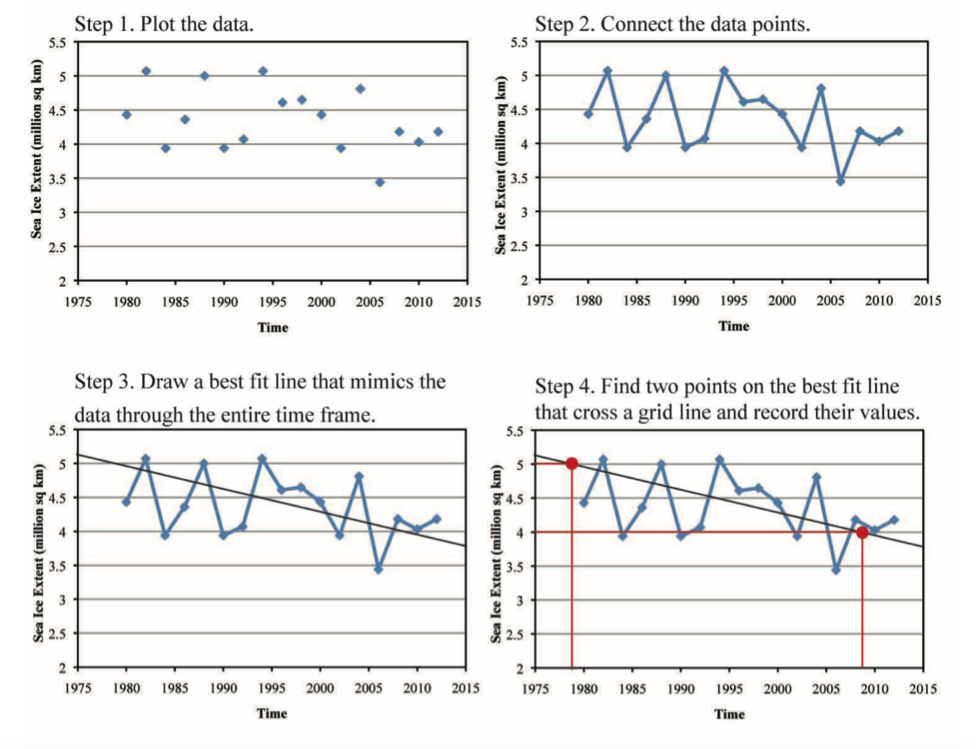
Now that you have completed the chart, plot the discharge against the recurrence interval on the graph template below. Please note that the x-axis (for recurrence interval) is in logarithmic scale and you may need to estimate where the data points fall. A logarithmic scale is non-linear, based on orders of magnitude. Draw a best-fit line through your data after all the points have been plotted. Make sure your best-fit line continues to the edge of the graph.
Interpreting your results
- On which date did a flood event have a recurrence interval of 0.5?
- 2/27/2013
- 10/13/2009
- 3/10/2011
- 4/20/2015
- Of the following dated flood events, which one would you expect to happen more often?
- 8/27/2008
- 2/24/2013
- 2/6/2010
- 12/23/2013
- Observe your best-fit line. What approximate discharge would be associated with a 50-year recurrence interval?
- 2,000 cfs
- 4,750 cfs
- 8,500 cfs
- 14,000 cfs
- Flood stage, or bankfull stage, on Sweetwater Creek occurs at a discharge of ~4,500 cfs. According to your best-fit line, what is the recurrence interval of such a discharge?
- 0.5 years
- 3 years
- 25 years
- 50 years
- During the flood event of 9/23/2009, the discharge measured at this gaging station was 21,200 cfs. Note where this would plot on your graph. Would the recurrence interval for this flood plot at:
- 100 years
- 300 years
- 700 years longer than
- 1,000 years
- Is it possible that a flood with a similar discharge to that of the event from 9/23/2009 could happen again in the next 20 years?
- Yes
- No
Grading
10 points: Accurately responded to each question, including a clearly drawn figure of Earth’s interior, a well-written brief summary, and showing the math for each of the 3 calculations. Any sources used were cited.
8 points: Responded to each question, but may have addressed one or two incorrectly.
5 points: More than two questions missed or answered incorrectly; sources were not cited.
2 points: Only very partial information provided.
0 points: Did not complete the assignment.

