1B: Faults
- Page ID
- 1334
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Faults are shear fractures or tabular zones with measurable displacement. As this displacement accumulates, faults tend to form a zone of fractured rock around them, called a damage zone, and form a zone of fault gouge along the slip surface. Thus, faults with significant offset appear very different from joints.
Some faults are obvious because of offset bedding or the presence of a damage zone and fault gouge. Active faults can often be identified because they disrupt the landscape, forming scarps that offset a previously continuous land surface. Offsets of the Earth's surface can also form across inactive faults if the fault juxtaposes two lithologies of different erodability. Sometimes, faults are only identifiable due to missing or repeated strata across an exposure or in a drill hole.
Fault Classification
Faults are classified by the orientation of the fault plane relative to the surface and the relative offset of the fault blocks.
Faults are categorized by dip, the angle of the fault plane relative to horizontal. Low angle faults have a dip of less than 45 degrees; high angle faults have a dip of greater than 45 degrees; and vertical faults are perpendicular to horizontal, with a dip angle of approximately 90 degrees.
Faults also have two categories of slip: normal or reverse, accommodating extension and shortening respectively; and sinistral or dextral, indicating relative motion of fault blocks parallel to the Earth's surface. A fault can have purely one type of slip or a combination of normal or reverse and strike-slip motion, producing an oblique sense of slip. If slip rates vary along a normal or reverse fault, that fault will have a rotational sense of slip.
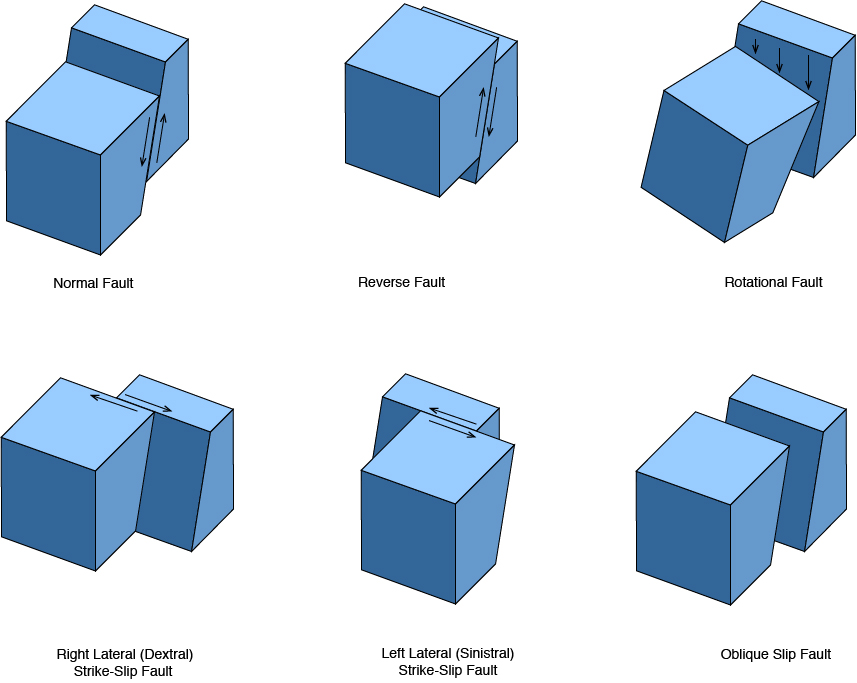
The Slip Vector
The slip vector of a fault can be broken into a number of components:
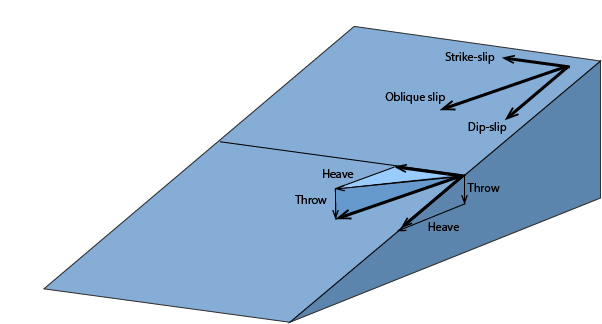
The oblique slip, or true slip on a fault, can be broken into two components in the plane of the fault: the dip-slip and strike-slip vectors. The strike-slip vector is the component of fault slip along strike, and the dip-slip is the component of motion in the plane of the fault that is perpendicular to fault strike. A fault with purely strike-slip motion has a dip-slip component of zero. A fault with purely normal or reverse slip has a strike-slip component of zero.
The dip-slip component can be further broken down into horizontal and vertical components, called heave and throw. The throw represents the entire vertical component of motion across a fault plane; the total horizontal component is the sum of the heave and strike-slip components.
Separation v. Slip
Separation is apparent fault slip from a displaced feature and is not always the same as the true slip vector. Planar features such as angled bedding can be deceptive, producing apparent lateral offset across a fault when only normal slip has actually occurred. To determine the true slip vector, either offset of a planar feature must be combined with kinematic information from the fault; or the offset of a linear feature, called a piercing line, must be measured instead.
Kinematic Indicators and Fault Zone Features
Slickenlines are fine ridges, grooves, or other striations on a fault plane that run parallel to fault slip. A fault surface with many slickenlines or a polished texture is called a slickenside. Mullions are subtle undulations of the fault plane which, like slickenlines, run parallel to the direction of fault slip.
Gouge is soft, powdery material on a fault plane created by the grinding of fault blocks as they slip. Fault motion can also create mixes of large, angular, broken rock pieces called breccias. When fault breccia solidifies, it is called cataclasite.
Drag folding near the fault may reveal the sense of shear. Caution is required, however, because similar-looking folds can also be produced by changes in fault dip.
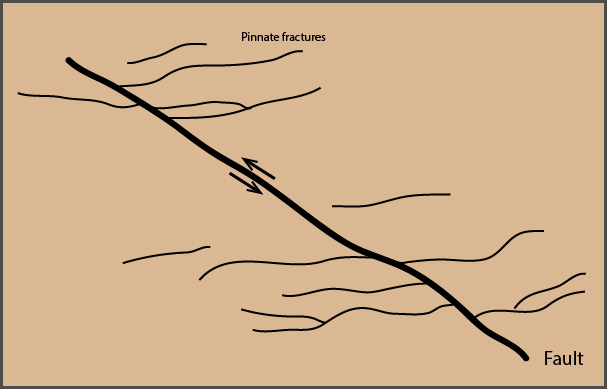
Pinnate fractures are mode I joints formed adjacent to fault zones, similar to tension gashes but lacking mineral-filled voids and rotation. These fractures indicate the sense of shear on the fault.
Fault Bends and Stepovers
Though faults themselves are generally simple, planar features, complex geometries arise where faults interact.
A double bend is a simple type of strike-slip fault stepover.
When a right-lateral strike-slip fault steps right or a left-lateral strike-slip fault steps left, an extensional bend is formed. Where a right-lateral fault steps left or a left-lateral fault steps right, a contractional bend forms.
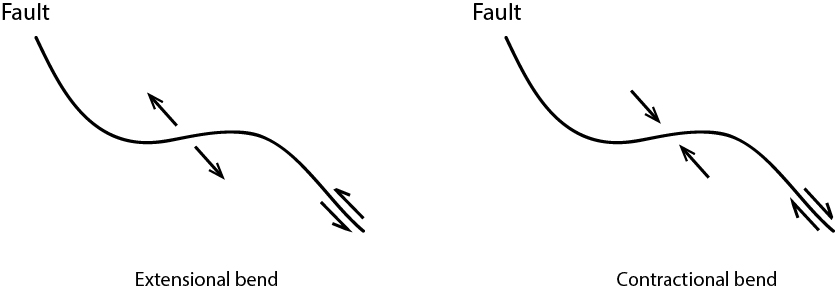
These bends are analogous to extensional and contractional ramp structures in normal and reverse faults.
Fault stepovers may feature structures such as extension fractures, rotated blocks, isolated lenses, and connecting faults. In a stepover, however, faults need not be connected in any simple way.
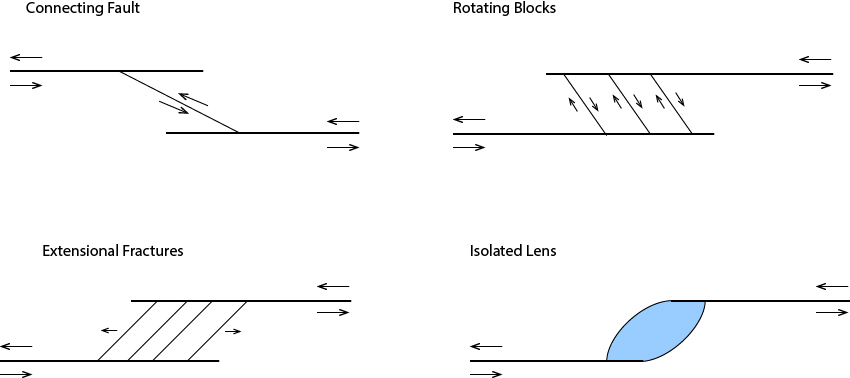
Duplexes
A duplex is a sliver or collection of slivers of rock in a fault zone where each sliver, called a horse, is bounded by faults. The isolated lenses discussed in the previous section are one variety of duplex. Duplexes commonly form in response to fault slip over double bends.
Fault Termination
Fault planes do not extend infinitely. Except where one fault intersects another, faults must end both at the surface and within the earth. A number of different fault termination styles exist to distribute deformation at the end of a fault:
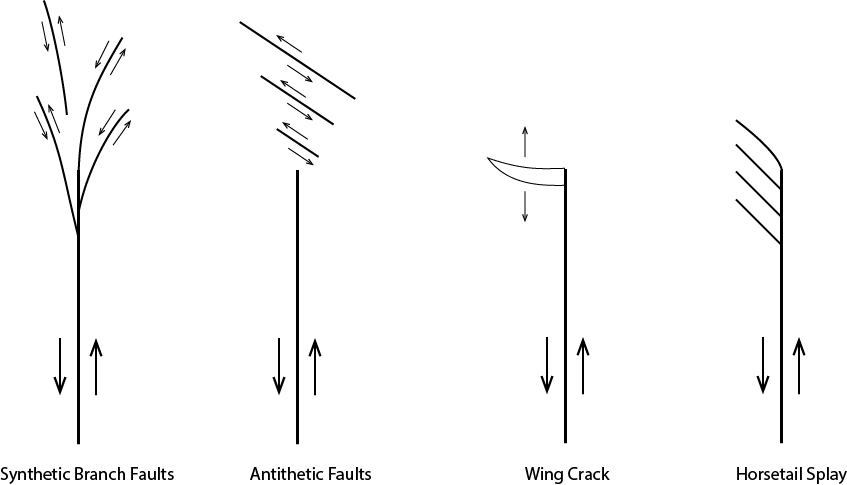
Synthetic faults have the same sense of slip as a larger related fault. Antithetic faults have the opposite sense of slip as a larger related fault. Synthetic and antithetic can also be used to describe the dip of small normal or reverse faults relative to larger faults of the same type in the area.
Summary
List of Terms
- Fault
- Damage zone
- Fault gouge
- Normal fault
- Reverse fault
- Strike-slip fault
- Dextral
- Sinistral
- Oblique slip vector
- Strike-slip vector
- Dip-slip vector
- Heave
- Throw
- Separation
- Piercing line
Contributors
Michael E. Oskin (Department of Earth and Planetary Sciences, UC Davis)


