5.7.9: Probabilistic Forecasting
- Page ID
- 6014
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview
We turn now to probabilistic forecasting. Examples of probability are:
- The chance of your winning the lottery,
- The chance of your being struck in a head-on collision on the freeway, or
- The chance that your house will be destroyed by fire.
Even though you don’t know if you will win the lottery or have your house burn down, the probability or likelihood of these outcomes is sufficiently well known that lotteries and gambling casinos can operate at a profit. You can buy insurance against a head-on collision or a house fire at a low enough rate that it is within most people’s means, and the insurance company can show a profit (see Chapter 10).
In the probabilistic forecasting of earthquakes, we use geodesy, geology, paleoseismology, and seismicity to consider the likelihood of a large earthquake in a given region or on a particular fault sometime in the future. A time frame of thirty to fifty years is commonly selected because that is close to the length of a home mortgage and is likely to be within the attention span of political leaders and the general public. A one-year time frame would yield a probability too low to get the attention of the state legislature or the governor, whereas a one-hundred-year timeframe, longer than most life spans, might not be taken seriously, even though the probability would be much higher.
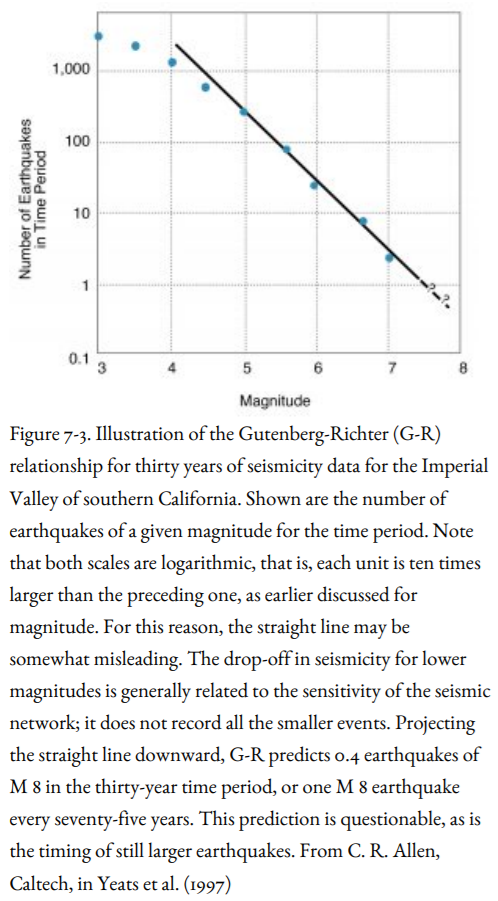
In 1954, Beno Gutenberg and Charles Richter of Caltech studied the instrumental seismicity of different regions around the world and observed a systematic relationship between magnitude and frequency of small-to-intermediate-size earthquakes. Earthquakes of a given magnitude interval are about ten times more frequent than those of the next higher magnitude (Figure 7-3). The departure of the curve from a straight line at low magnitudes is explained by the inability of seismographs to measure very small earthquakes. These small events would only be detected when they are close to a seismograph; others that are farther away would be missed. So Gutenberg and Richter figured that if the seismographs could measure all the events, they would fall on the same straight line as the larger events that are sure to be detected, no matter where they occur in the region of interest. Note that Figure 7-3 is logarithmic, meaning that larger units are ten times as large as smaller ones.
This is known as the Gutenberg-Richter (G-R) relationship for a given area. If the curve is a straight line, then only a few years of seismograph records of earthquakes of low magnitude could be extrapolated to forecast how often earthquakes of larger magnitudes not covered by the data set would occur.
A flaw in the assumptions built into the relationship (or, rather, a misuse of the relationship unintended by Gutenberg and Richter) is that the line would continue to be straight for earthquakes much larger than those already measured. For example, if the Gutenberg-Richter curve predicted one M 7 earthquake in ten years for a region, this would imply one M 8 per one hundred years, one M 9 per one thousand years, and one M 10 per ten thousand years! Clearly this cannot be so, because no earthquake larger than M 9.5 is known to have occurred. Clarence Allen of Caltech has pointed out that if a single fault ruptured all the way around the Earth, an impossible assumption, the magnitude of the earthquake would be only 10.6. So the Gutenberg-Richter relationship, used (or misused) in this way, fails us where we need it the most, in forecasting the frequency of the largest earthquakes that are most devastating to society.
Roy Hyndman and his associates at Pacific Geoscience Centre constructed a Gutenberg-Richter curve for crustal earthquakes in the Puget Sound and southern Georgia Strait regions (Figure 7-4). The time period of their analysis is fairly short because only in the past twenty years has it been possible to separate crustal earthquakes from those in the underlying Juan de Fuca Plate. They have reliable data for earthquakes of magnitudes 3.5 to 5 and less reliable data for magnitudes up to about 6.2. The frequency curve means one earthquake of magnitude 3.6 every year and 0.1 earthquakes of magnitude 5.1 every year (or one earthquake of that magnitude every ten years). Extending the curve as a straight line would predict one earthquake of magnitude 6 every fifty years.
Hyndman and his colleagues followed modern practice and did not extrapolate the G-R relationship as a straight line to still higher magnitudes. They showed the line curving downward to approach a vertical line, which would be the maximum magnitude, which they estimated as M 7.3 to 7.7. This would lead to an earthquake of magnitude 7 every four hundred years. Other estimates based on the geology lead to a maximum magnitude (MCE) of 7.3, a deterministic estimate. Assuming that most of the GPS-derived -crustal shortening between southern Washington and southern British Columbia takes place by earthquakes, there should be a crustal earthquake in this zone every four hundred years. The last earthquake on the Seattle Fault struck about eleven hundred years ago, but it is assumed that other faults in this region such as the Tacoma Fault or Southern Whidbey Island Fault might make up the difference. Thus geology and tectonic geodesy give estimates comparable to the Gutenberg-Richter estimate for M 7 earthquakes as long as G-R does not follow a straight line for the highest magnitudes.
This analysis works for Puget Sound and the Georgia Strait, where there is a large amount of instrumental seismicity. It assumes that the more earthquakes recorded on seismograms, the greater the likelihood of much larger earthquakes in the future. Suppose your region had more earthquakes of magnitudes below 7 than the curve shown in Figure 7-3. This would imply a larger number of big earthquakes and a greater hazard. At first, this seems logical. If you feel the effects of small earthquakes from time to time, you are more likely to worry about bigger ones.
Yet the instrumental seismicity of the San Andreas Fault leads to exactly the opposite conclusion. Those parts of the San Andreas Fault that ruptured in great earthquakes in 1857 and 1906 are seismically very quiet today. This is illustrated in Figure 7-5, a seismicity map of central California, with the San Francisco Bay Area in its northwest corner. The San Andreas Fault extends from the upper left to the lower right corner of this map. Those parts of the San Andreas Fault that release moderate-size earthquakes frequently, like Parkfield and the area northwest of Parkfield, stand out on the seismicity map. The fault is weakest in this area, and it is unlikely to store enough strain energy to release an earthquake as large as magnitude 7. However, the fault in the northwest corner of the map (part of the 1906 rupture of M 7.9) has relatively low instrumental seismicity, and the fault in the southeast corner (part of the 1857 rupture, also M 7.9) is not marked by earthquakes at all. The segments of the fault with the lowest instrumental seismicity have the potential for the largest earthquake, almost a magnitude 8.
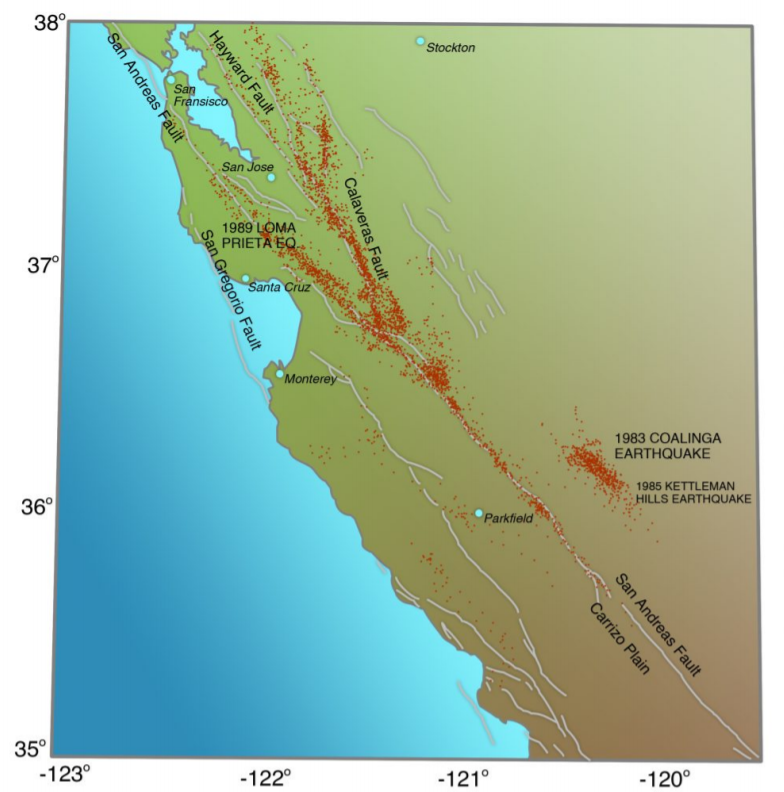

The Cascadia Subduction Zone has essentially zero instrumental seismicity north of California (Figure 4-13). Yet geological evidence and comparisons with other subduction zones provide convincing evidence that Cascadia has ruptured in earthquakes as large as magnitude 9, the last in January 1700.
This shows that the Gutenberg-Richter extrapolation to higher magnitudes works in those areas where there are many small- to moderate-size earthquakes, but not where the fault is completely locked. Seismicity, which measures the release of stored elastic strain energy, depends on the strength of the crust being studied. A relatively weak fault like the San Andreas Fault at Parkfield would have many small earthquakes because the crust could not store enough strain to release a large one. A strong fault like the San Andreas Fault north of San Francisco would release few or no earthquakes until strain had built up enough to rupture the crust in a very large earthquake, such as the earthquake of April 18, 1906.
Paleoseismology confirms the problems in using the Gutenberg-Richter relationship to predict the frequency of large earthquakes. Dave Schwartz and Kevin Coppersmith, then of Woodward-Clyde Consultants in San Francisco, were able to identify individual earthquakes in backhoe trench excavations of active faults in Utah and California based on fault offset of sedimentary layers in the trenches. They found that fault offsets tend to be about the same for different earthquakes in the same backhoe trench, suggesting that the earthquakes producing the fault offsets tend to be about the same size. This led them to the concept of characteristic earthquakes: a given segment of fault tends to produce the same size earthquake each time it ruptures to the surface. This would allow us to dig backhoe trenches across a suspect fault, determine the slip on the last earthquake rupture (preferably on more than one rupture event), and forecast the size of the next earthquake. When compared with the Gutenberg-Richter curve for the same fault, which is based on instrumental seismicity, the characteristic earthquake might be larger or smaller than the straight-line extrapolation would predict. Furthermore, the Gutenberg-Richter curve cannot be used to extrapolate to earthquake sizes larger than the characteristic earthquake. The characteristic earthquake is as big as it ever gets on that particular fault.
Before we get too impressed with the characteristic earthquake idea, it must be said that where the paleoseismic history of a fault is well known, like that part of the San Andreas Fault that ruptured in 1857, some surface-rupturing earthquakes are larger than others, another way of saying that not all large earthquakes on the San Andreas Fault are characteristic. Similarly, although we agree that the last earthquake on the Cascadia Subduction Zone was a magnitude 9, the evidence from subsided marshes at Willapa Bay, Washington (Figure 4-10a) and from earthquake-generated turbidites (Figure 4-9) suggests that some of the earlier ones may have been smaller or larger than an M 9.
This discussion suggests that no meaningful link may exist between the Gutenberg-Richter relationship for small events and the recurrence and size of large earthquakes. For this relationship to be meaningful, the period of instrumental observation needs to be thousands of years. Unfortunately, seismographs have been running for only a little longer than a century, so that is not yet an option.
Before considering a probabilistic analysis for the San Francisco Bay Area in northern California, it is necessary to introduce the principle of uncertainty. There is virtually no uncertainty in the prediction of high and low tides, solar or lunar eclipses, or even the return period of Halley’s Comet. These events are based on well-understood orbits of the Moon, Sun, and other celestial bodies. Unfortunately, the recurrence interval of earthquakes is controlled by many variables, as we learned at Parkfield. The strength of the fault may change from earthquake to earthquake. Other earthquakes may alter the buildup of strain on the fault, as the 1983 Coalinga Earthquake might have done for the forecasted Parkfield Earthquake that did not strike in 1988. Why does one tree in a forest fall today, but its neighbor of the same age and same growth environment takes another hundred years to fall? That is the kind of uncertainty we face with earthquake forecasting.
How do we handle this uncertainty? Figure 7-6 shows a probability curve for the recurrence of the next earthquake in a given area or along a given fault. Time in years advances from left to right, starting at zero at the time of the previous earthquake. The chance of an earthquake at a particular time since the last earthquake increases upward at first. The curve is at its highest at that time we think the earthquake is most likely to happen (the average recurrence interval), and then the curve slopes down to the right. We feel confident that the earthquake will surely have occurred by the time the curve drops to near zero on the right side of the curve.
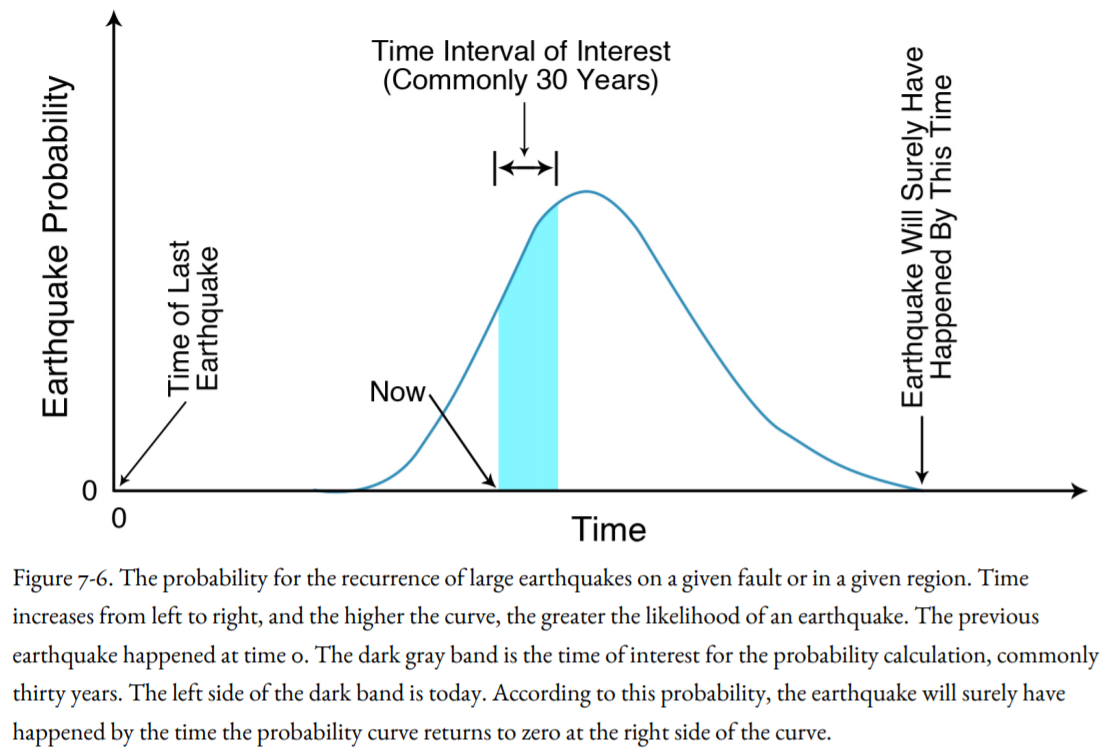
The graph in Figure 7-6 has a darker band, which represents the time frame of interest in our probability forecast. The left side of the dark band is today, and the right side is the end of our time frame, commonly thirty years from now, the duration of most home mortgages. There is a certain likelihood that the earthquake will occur during the time frame we have selected.
This is similar to weather forecasting, except we are talking about a thirty-year forecast rather than a five-day forecast. If the meteorologist on the six-o’clock news says there is a 70 percent chance of rain tomorrow, this also means that there is a 30 percent chance that it will not rain tomorrow. The weather forecaster is often “wrong” in that the less likely outcome actually comes to pass. The earthquake forecaster also has a chance that the less-likely outcome will occur, as was the case for the 1988 Parkfield forecast.
Imagine turning on TV and getting the thirty-year earthquake forecast. The TV seismologist says, “There is a 70 percent chance of an earthquake of magnitude 6.7 or larger in our region in the next thirty years.” People living in the San Francisco Bay Area actually received this forecast in October 1999, covering a thirty-year period beginning in January 2000. That might not affect their vacation plans, but it should affect their building codes and insurance rates. It also means that the San Francisco Bay Area might not have an earthquake of M 6.7 or larger in the next thirty years (Figure 7-7). More about that forecast later.
How do we draw our probability curve? We consider all that we know: the frequency of earthquakes based on historical records and geologic (paleoseismic) evidence, the long-term geologic rate at which a fault moves, and so on. A panel of experts is convened to debate the various lines of evidence and arrive at a consensus, called a logic tree, about probabilities. The debate is often heated, and agreement may not be reached in some cases. We aren’t even sure that the curve in Figure 7-6 is the best way to forecast an earthquake. The process might be more irregular, even chaotic.
Our probability curve has the shape that it does because we know something about when the next earthquake will occur, based on previous earthquake history, fault slip rates, and so on. But suppose that we knew nothing about when the next earthquake would occur; that is to say, our data set had no “memory” of the last earthquake to guide us. The earthquake would be just as likely to strike one year as the next, and the probability “curve” would be a straight horizontal line. This is the same probability that controls your chance of flipping a coin and having it turn up heads: 50 percent. You could then flip the coin and get heads the next five times, but the sixth time, the probability of getting heads would be the same as when you started: 50 percent.
However, our probability curve is shaped like a bell; it “remembers” that there has been an earthquake on the same fault or in the same region previously. We know that another earthquake will occur, but we are unsure about the displacement per event or the long-term slip rate, and nature builds in additional uncertainty. The broadness of this curve builds in all these uncertainties.
Viewed probabilistically, the Parkfield forecast was not really a failure; the next earthquake is somewhere on the right side of the curve. We are sure that there will be another Parkfield Earthquake, but we don’t know when the right side of the curve will drop down to near zero. Time 0 is 1966, the year of the last Parkfield Earthquake. The left side of the dark band is today. Prior to 1988, when the next Parkfield Earthquake was expected, the high point on the probability curve would have been in 1988. The time represented by the curve above zero would be the longest recurrence interval known for Parkfield, which would be thirty-two years, the time between the 1934 and 1966 earthquakes. That time is long past; the historical sample of earthquake recurrences at Parkfield, although more complete than for most faults, was not long enough. The next Parkfield earthquake actually occurred in 2004, which would have been to the right of the dark band in Figure 6-6 and possibly to the right of the zero lines in that figure.
How about the next Cascadia Subduction Zone earthquake? Time 0 is A.D. 1700 when the last earthquake occurred. The left edge of the dark band is today. Let’s take the width of the dark band as thirty years, as we did before. We would still be to the left of the high point in the probability curve. Our average recurrence interval based on paleoseismology is a little more than five hundred years, and it has only been a bit more than three hundred years since the last earthquake. What should be the time when the curve is at zero again? Not five hundred years after 1700 because paleoseismology (Figures 4-9, 4-21) shows that there is great variability in the recurrence interval. The earthquake could strike tomorrow, or it could occur one thousand years after 1700, or A.D. 2700.


