5.3.6: Measuring an Earthquake
- Page ID
- 5921
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Magnitude
The chorus of high-frequency and low-frequency seismic waves that radiate out from an earthquake indicates that no single number can characterize an earthquake, just as no single number can be used to describe a Yakima Valley wine or a sunset view of Mt. Rainier or Mt. Hood.
The size of an earthquake was once measured largely on the basis of how much damage was done. This was unsatisfactory to Caltech seismologist Charles Richter, who wanted a more quantitative measure of earthquake size, at least for southern California. Following up on earlier work done by the Japanese, Richter in 1935 established a magnitude scale based on how much a seismograph needle is deflected by a seismic wave generated by an earthquake about sixty miles (a hundred kilometers) away (Figure 3-14). Richter used a seismograph specially designed by seismologist Harry Wood and astronomer John Anderson to record local earthquakes in southern California. This seismograph was best suited for those waves that vibrated with a frequency of about five times per second, which is a bit like measuring how loud an orchestra is by how loud it plays middle C. Nonetheless, it enabled Richter and his colleagues to distinguish large, medium-sized, and small earthquakes in California, which was all they wanted to do. Anderson was an astronomer, and the seismograph was built at the Mt. Wilson Observatory, which may account for the word magnitude, a word that also expresses how bright a star is.
Complicating the problem for the layperson is that Richter’s scale is logarithmic, which means that an earthquake of magnitude 5 would deflect the needle of the Wood-Anderson seismograph ten times more than an earthquake of magnitude 4 (Figure 3-14). And an increase of one magnitude unit represents about a thirty-fold increase in the release of stored-up seismic strain energy. So the Olympia, Washington, Earthquake of 7.1 on April 13, 1949, would be considered to have released the energy of more than thirty earthquakes the size of the Klamath Falls, Oregon, Earthquake of September 20, 1993, which was magnitude 6.

Richter never claimed that his magnitude scale, now called local magnitude and labeled ML, was an accurate measure of earthquakes. Nonetheless, the Richter magnitude scale caught on with the media and the general public, and it is still the first thing that a reporter asks a professional about an earthquake: “How big was it on the Richter scale?” The Richter magnitude scale works reasonably well for small to moderate-size earthquakes, but it works poorly for very large earthquakes, the ones we call great earthquakes. For these, other magnitude scales are necessary.
To record earthquakes at seismographs thousands of miles away, seismologists had to use long-period (low frequency) waves, because the high-frequency waves recorded by Richter on the Wood-Anderson seismographs die out a few hundred miles away from the epicenter. To understand this problem, think about how heavy metal music is heard a long distance away from its source, a live band or a boom box. Sometimes when my window is open on a summer evening, I can hear a faraway boom box in a passing car, but all I can hear are the very deep, or low frequency, tones of the bass guitar, which transmit through the air more efficiently than the treble (high-frequency) guitar notes or the voices of the singers. In this same way, low-frequency earthquake waves can be recorded thousands of miles away from the earthquake source, so that we were able to record the magnitude 9 Tohoku-oki earthquake in Japan on our seismograph in Corvallis, Oregon. Low-frequency body waves pass through the Earth and are used to study its internal structure, analogous to X-rays of the human body. A body-wave magnitude is called mb.
A commonly used earthquake scale is the surface wave magnitude scale, or MS, which measures the largest deflection of the needle on the seismograph for a surface wave that takes about twenty seconds to pass a point (which is about the same frequency as some ocean waves).
The magnitude scale most useful to professionals is the moment magnitude scale, or MW, which comes closest to measuring the true size of an earthquake, particularly a large one. This scale relates magnitude to the area of the fault that ruptures and the amount of slip that takes place on the fault. For many very large earthquakes, this can be done by measuring the length of the fault that ruptures at the surface and figuring out how deep the zone of aftershocks extends, thereby calculating the area of the rupture. The amount of slip can be measured at the surface as well. The seismologist can also measure MW by studying the characteristics of low-frequency seismic waves, and the surveyor or geodesist (see section 7 of this chapter) can measure it by remeasuring the relative displacement of survey benchmarks immediately after an earthquake to work out the distortion of the ground surface and envisioning a subsurface fault that would produce the observed distortion (see below).
For small- to intermediate-size earthquakes, the magnitude scales are designed so that there is relatively little difference between Richter magnitude, surface-wave magnitude, and moment magnitude. But for very large earthquakes, the difference is dramatic. For example, both the 1906 San Francisco Earthquake and the 1964 Alaska Earthquake had a surface-wave magnitude of 8.3. However, the San Francisco Earthquake had a moment magnitude of only 7.9, whereas the Alaska Earthquake had a moment magnitude of 9.2, which made it the second-largest earthquake of the twentieth century. The surface area of the fault rupture in the Alaska Earthquake was the size of the state of Iowa!
Intensity
Measuring the size of an earthquake by the energy it releases is all well and good, but it is still important to measure how much damage it does at critical places (such as where you or I or our loved ones happen to be when the earthquake strikes). This measurement is called earthquake intensity, which is measured by a Roman numeral scale (Table 3-1). Intensity III means no damage, and not everybody feels it. Intensity VII or VIII involves moderate damage, particularly to poorly constructed buildings, while Intensity IX or X causes considerable damage. Intensity XI or XII, which fortunately is rare, is characterized by nearly total destruction.
Earthquake intensities are based on a post-earthquake survey of a large area. Damage is noted, and people are questioned about what they felt. An intensity map is a series of concentric lines, irregular rather than circular, in which the highest intensities are generally (but not always) closest to the epicenter of the earthquake. For illustration, an intensity map is shown for the 1993 Scotts Mills Earthquake in the Willamette Valley of Oregon (Figure 3-15). High intensities were recorded near the epicenter, as expected. But intensity can also be influenced by the characteristics of the ground. Buildings on solid rock tend to fare better (and thus are subjected to lower intensities) than buildings on thick soft soil. The Intensity VI contour bulges out around the capital city of Salem, and the Intensity V contour bends south to include the city of Albany. Both are along the Willamette River (dotted line in Figure 3-15), where soft river deposits increased strong shaking. The effect of soft soils is discussed further in Chapter 8.
| Modified Mercalli Intensity Scale |
| I | Not felt except by a very few, under especially favorable circumstances. |
| II | Felt only by a few persons at rest, especially on upper floors of buildings. Delicately suspended objects may swing |
| III | Felt quite noticeably indoors, especially on upper floors of buildings, but many people do not recognize it as an earthquake. Standing automobiles may rock slightly. Vibrations like the passing of a truck. |
| IV | During the day, felt indoors by many, outdoors by few. At night, some awakened. Dishes, windows, doors disturbed; walls make a creaking sound. Sensation like heavy truck striking building. Standing automobiles rocked noticeably. |
| V | Felt by nearly everyone; many awakened. Some dishes, windows, etc. broken; cracked plaster in a few places; unstable objects overturned. Disturbance of trees, poles, and other tall objects sometimes noticed. Pendulum clocks may stop. |
| VI | Felt by all, many frightened and run outdoors. Some heavy furniture moved; a few instances of fallen plaster and damaged chimneys. Damage slight; masonry D cracked. |
| VII | Everybody runs outdoors. Damage negligible in buildings of good design and construction; slight to moderate in well-built ordinary structures; considerable in poorly built or badly designed structures (masonry D); some chimneys will be broken. Noticed by persons driving cars. |
| VIII | Damage slight in a specially designed structure; no damage to masonry A, some damage to masonry B, considerable damage to masonry C with partial collapse. Panel walls will be thrown out of frame structures. Fall of chimneys, factory stacks, columns, monuments, walls. Frame houses moved off foundations if not bolted. Heavy furniture overturned. Sand and mud ejected in small amounts. Changes in well water. Persons driving cars disturbed. |
| IX | Damage considerable in specially designed structures; well-designed frame structures thrown out of plumb; great in substantial buildings, with partial collapse. Masonry B seriously damaged, masonry C heavily damaged, some with partial collapse, Masonry D destroyed. Buildings shifted off foundations. The ground cracked conspicuously. Underground pipes will be broken. |
| X | Some well-built wooden structures destroyed; most masonry and frame structures destroyed with foundations; ground badly cracked. Rails bent. Landslides will be considerable from river banks and steep slopes. Shifted sand and mud. Water splashed over banks. |
| XI | Few, if any, masonry structures remain standing. Bridges destroyed. Broad fissures in the ground. Underground pipelines completely out of service. Earth slumps and landslips in soft ground. Rails bent greatly. |
| XII | Damage total. Waves can be seen on the ground surface. Lines of sight and level distorted. Objects will be thrown into the air. |
| Masonry A | Good workmanship, mortar, and design; reinforced, especially laterally, and bout together using steel, concrete, etc. |
| Masonry B | Good workmanship and mortar, reinforce, but not designed in detail to resist lateral forces. |
| Masonry C | Ordinary workmanship and mortar, no extreme weakness like failing to tie in at corners, but neither reinforced nor designed against horizontal forces. |
| Masonry D | Weak materials such as adobe; poor mortar, low standards of workmanship, weak horizontally |
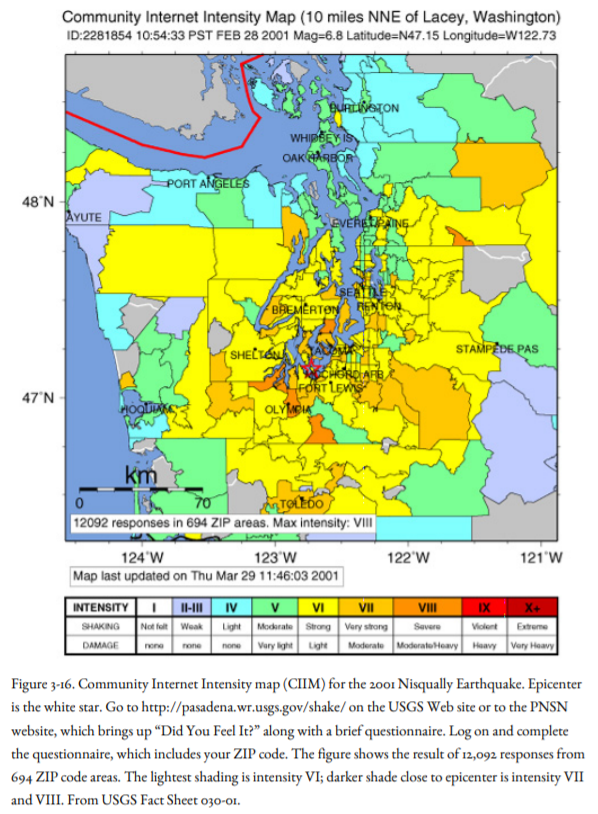
In the Pacific Northwest, creating an intensity map by the use of questionnaires is now done on the Internet. You can contribute to science. If you feel an earthquake, go to http://www.ess.washington.edu and click on Pacific Northwest Earthquakes, which will take you to the Pacific Northwest Seismograph Network. Click on Report an Earthquake. This brings up the phrase, Did You Feel It? Click on your state and you can fill out a report and submit it electronically. The resulting map shows intensity in color, by zip code, and is called the Community Internet Intensity Map (CIIM). Figure 3-16 shows the CIIM for the 2001 Nisqually Earthquake. An earthquake of M 3.7 near Bremerton, Washington, on May 29, 2003, drew more than one thousand responses in the first twenty-four hours.
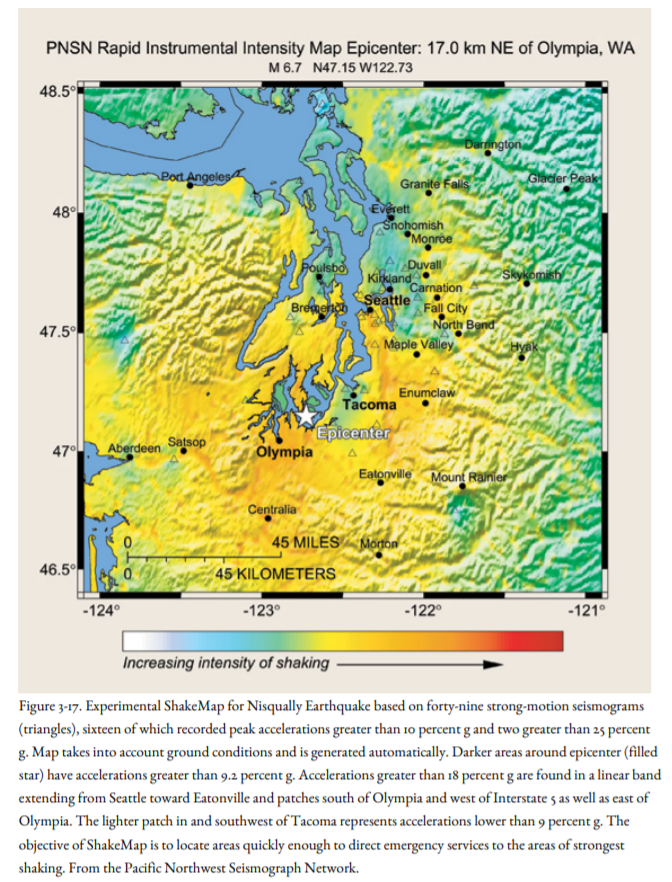
Figure 3-17 relates earthquake intensity to the maximum amount of ground acceleration (peak ground acceleration, or PGA) that is measured with a special instrument called a strong-motion accelerograph. Acceleration is measured as a percentage of the Earth’s gravity. A vertical acceleration of one g would be just enough to lift you (or anything else) off the ground. Obviously, this would have a major impact on the damage done by an earthquake at a given site. Peak ground velocity (PGV) is also routinely measured.
The Internet-derived intensity map is not generated fast enough to be of use to emergency managers, who need to locate quickly the areas of highest intensity, and thus the areas where damage is likely to be greatest. What resources must be mobilized, and where should they be sent? The TriNet Project was developed for southern California by the U.S. Geological Survey (USGS), Caltech, and the California Geological Survey with support from the Federal Emergency Management Agency (FEMA), taking advantage of a large number of strong-motion seismographs in the state, a detailed knowledge of active faults of the region, and of soil types likely to result in high accelerations. After the Northridge Earthquake of 1994, this project developed ShakeMap, which takes the calculated magnitude, depth, causative fault, direction of rupture propagation, and soil types to produce an intensity map within five minutes of the earthquake. The ShakeMap software was installed at the Pacific Northwest Seismograph Network at the University of Washington in January 2001, one month before the Nisqually Earthquake, and was still in test mode when that earthquake struck. The ShakeMap for this earthquake, which was made available to the public one day after the earthquake, is shown as Figure 3-17. You can access a ShakeMap, even for smaller earthquakes, through http://www.trinet.org/shake or through the Pacific Northwest Seismograph Network website.
As pointed out above, Intensities VII and VIII may result in major damage to poorly constructed buildings whereas well-constructed buildings should ride out those intensities with much less damage. This points out the importance of earthquake-resistant construction and strong building codes, discussed further in Chapters 11 and 12. Except for adobe, nearly all buildings will ride out intensities of VI or less, even if they are poorly constructed. For the rare occasions when intensities reach XI or XII, many buildings will fail, even if they are well constructed. But for the more common intensities of VII through X, earthquake-resistant construction will probably mean the difference between collapse of the building, with loss of life, and survival of the building and its inhabitants.
Measurements of intensity are the only way to estimate the magnitudes of historical earthquakes that struck before the development of seismographs. Magnitude estimates based on intensity data have been made for decades, but these were so subjective that magnitude estimates and epicenter locations made in this way were unreliable. For example, the epicenter of the poorly understood earthquake of December 14, 1872, has been placed at many locations in northeastern Washington and even in southern British Columbia, with magnitude estimates as high as M 7.4. Can these estimates be made more quantitative, and thereby more useful in earthquake hazard estimates?
Bill Bakun and Carl Wentworth of the USGS figured out a way to do it. First, they had to cope with the behavior of seismic waves passing through parts of the Earth that react to seismic waves in different ways. Seismic waves die out (attenuate) more rapidly in some parts of the Earth than in others. It’s like hitting a sawed log with a hammer and listening for the sound at the other end. If the wood is good, the hammer makes a clean sound. If the wood is rotten, however, the hammer goes “thunk”. By measuring the attenuation (“thunkiness”) and wave speeds of more recent earthquakes that have had magnitudes determined by seismographs, Bakun and Wentworth were able to calibrate the behavior of the Earth’s crust in the vicinity of pre-instrumental earthquakes in the same region. The magnitude measured in this way is called intensity magnitude, or MI.
Bakun teamed with several colleagues, including Ruth Ludwin of the University of Washington and Margaret Hopper of the USGS, who had already done a study of the 1872 earthquake, and analyzed twentieth-century earthquakes with instrumentally determined magnitudes both east and west of the Cascades to take into account the different behavior of the Earth’s crust in western as compared to eastern Washington. They compared the intensities from these modern earthquakes with the intensities reported from the 1872 earthquake at seventy-eight locations to find the epicenter and magnitude that best matched the pattern of intensity observed in 1872. The earthquake, they determined, was located south of Lake Chelan with MI estimated as 6.8. (This earthquake is discussed further in Chapter 6.)
Fault-Plane Solutions
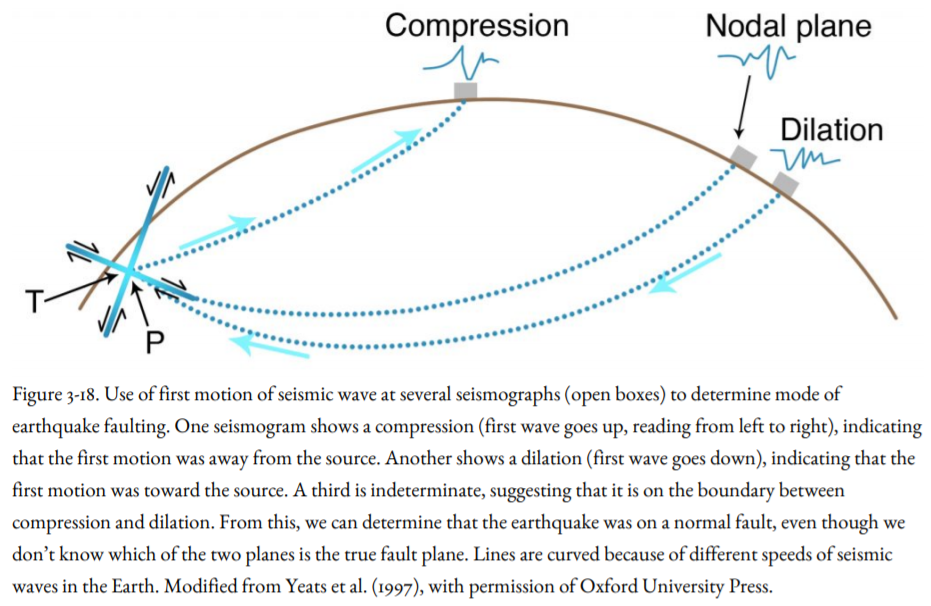
In the early days of seismography, it was enough to locate an earthquake accurately and to determine its magnitude. But seismic waves contain much more information, including the determination of the type of faulting. The seismogram shows that the first motion of an earthquake P-wave is either a push toward the seismograph or a pull away from it. With the modern three-component networks in the Northwest and adjacent parts of Canada, it is possible to determine the push or pull relationship at many stations, leading to information about whether the earthquake is on a reverse fault, a normal fault, or a strike-slip fault (as illustrated in Figure 3-18, which indicates the earthquakes was on a normal fault in which the earthquakes wave pushed outward horizontally from the hypocenter, similar to the 1993 Klamath Falls Earthquake). Most earthquakes are not accompanied by surface faulting, so the fault-plane solutions are the best evidence of the type of fault causing the earthquake. The fault generating the September 1993 Klamath Falls, Oregon, Earthquakes did not rupture the surface, but their fault-plane solutions showed that they were caused by rupture of a normal fault striking approximately north-northwest, in agreement with the local geology (for further discussion, see Chapter 6). Seismic waves recorded digitally on broadband seismographs are able to record many frequencies of seismic waves. These can be analyzed to show that an earthquake may consist of several ruptures within a few seconds of each other, some with very different fault plane solutions.