7.3.4: Special Problems
- Page ID
- 6275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview
Each large building presents its own set of design problems in surviving earthquake forces, which means that architects must consider earthquake shaking in designing a large structure in a seismically hazardous region such as the Pacific Northwest. I consider the problem of a soft ground floor and the issue of the tuning fork.

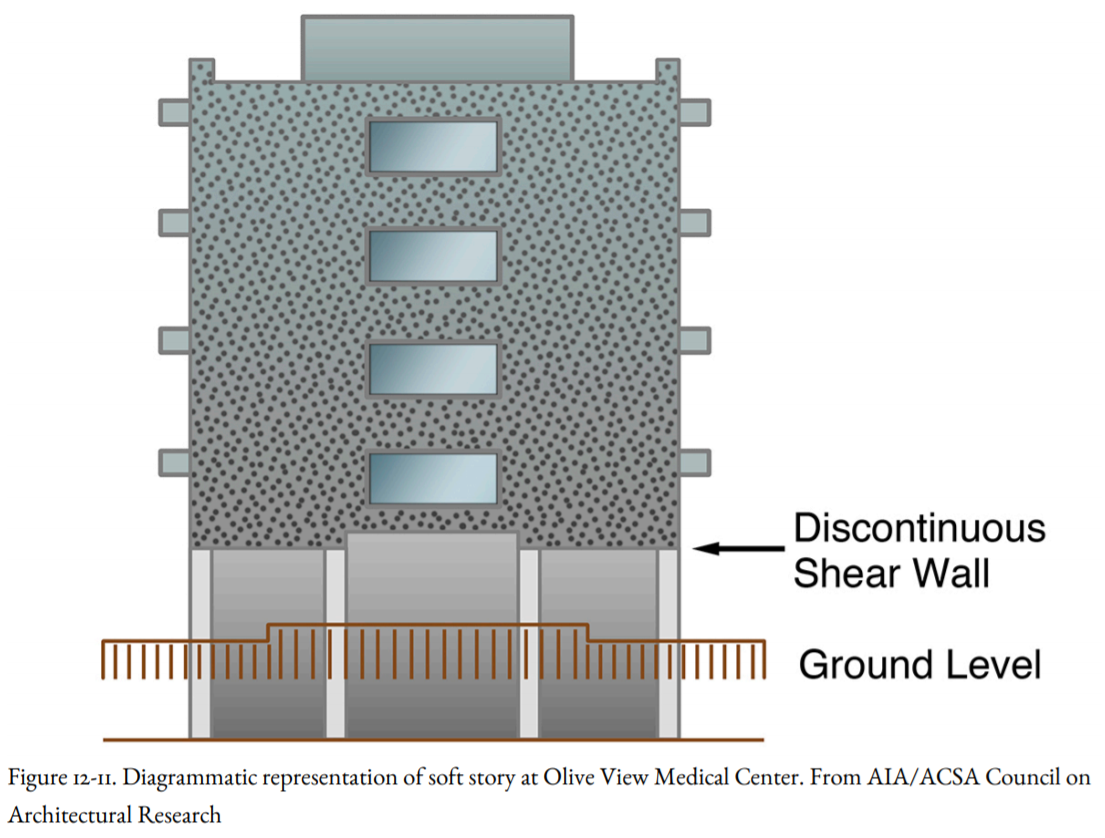
In a building with a soft ground floor, the ground floor is weaker than the higher floors. The ground floor is taken up by a parking garage or contains large amounts of open space occupied by a department store or hotel ballroom. Instead of load-bearing walls, these spaces are supported by columns. Building codes commonly limit the height of soft stories to two normal stories, or thirty feet. But the result is that the ground floor is less stiff (has less strength) than the overlying floors. Since earthquake forces enter the building at its base and are strongest there, the soft ground floor is a “strength and stiffness discontinuity” that absorbs the force of the earthquake waves. Without a soft ground floor, the earthquake forces are distributed more equally throughout the entire building. With a soft ground floor, there is a tremendous concentration of forces on the ground floor and at the connection between the ground floor and the second floor. This can cause collapse or partial collapse of the higher floors, as happened at the Los Angeles County Olive View Medical Center during the 1971 Sylmar Earthquake (Figures 12-10 and 12-11). The upper floors were relatively undamaged, but the lowermost floor and basement absorbed much of the force. The acceleration came from the right, and the building was forced toward the right, almost knocking down the stairwell. The problem can be alleviated by adding more columns, stiffening the existing structure. A second problem is illustrated by Figure 12-12, in which apartments were constructed over a garage in the basement, which acted as a soft story.
This brings us to the tuning fork problem. A large pipe organ has pipes of different lengths so that the organ can play different notes. The deep bass notes are played on long pipes, and the high notes are played on short pipes. A xylophone works the same way: the high notes are played on short keys, and the low notes are played on long keys. These instruments are designed to take advantage of the vibrational frequency of the pipes or keys to make music. A tuning fork works in the same way. Strike the tuning fork and place it tines-up on a hard surface. You will hear a specific note, related to the length of the tuning fork, which generates sound waves of a specific frequency—the vibrational frequency of the tuning fork.

I recall a TV commercial in which a wine glass is shattered when a Wagnerian soprano sings a certain high note. Buildings work in the same way. A tall building vibrates at a lower frequency than a short building, just like a tuning fork. The problem comes when the earthquake wave transmitted through the ground vibrates at the same frequency as the building. The building resonates with the earthquake waves, and the amplitude of the waves is intensified. All other things being the same, a building with the same vibrational frequency as the earthquake waves will suffer more damage than other buildings of different height.
In the Mexico City Earthquake of 1985, surface waves with a period of about two seconds were amplified by the soft clay underlying most of the city, which also extended the period of strong shaking. Buildings between ten and fourteen stories suffered the greatest damage because they had a natural vibrational period of one to two seconds (Figure 12-13). When waves of that characteristic frequency pushed the foundations of those buildings sideways, the natural resonance caused an accentuation of the sideways shaking and resulted in great structural damage. In contrast, a thirty-seven-story building built in the 1950s, with a vibrational period of 3.7 seconds, suffered no major structural damage.



