17.1: Introduction to Planar Stratification
- Page ID
- 4260
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Planar stratification is just as common as cross-stratification, if not more so, but the literature on it is not nearly as large. In a sense, the title of this chapter is misleading: it concentrates on the topic of planar lamination, not planar stratification in general.
It seems important at the outset to mention the distinction between beds with approximately planar and parallel bases and tops, forming tabular sediment bodies (I tend to call such beds tabular beds rather than planar beds), on the one hand, and planar internal stratification, within much thicker beds, either planar or not, on the other hand. Such internal stratification might be either technically bedding or lamination, technically, depending on stratum thickness, but the important point is that the relatively thick bed typically comprises a very large number of much thinner internal laminae. This distinction seems to me to be useful and sensible.
We need to deal with some more matters of terminology. First of all, the term “parallel” does not need to imply that the existence of straight lines or planes: the laminae might be curved, in three dimensions, but they are parallel in the sense of being congruent; that is, adjacent laminae have the same shape, or are at least close to having the same shape. I prefer, however, to reserve the term parallel for laminae that are close to being planes, and to use the term congruent for laminae that do not form planes but have approximately the same curved shape in a succession of laminae.
As far as I can tell, the terms planar lamination and parallel lamination are essentially identical. Such lamination is sometimes also called even lamination or horizontal lamination, although the latter term may carry some confusion, because the laminae may have been horizontal when deposited but are not now, or they could have been deposited with a non-negligible initial dip even though they were planar.
One could develop a geometrical classification of laminae in a lamina set (also called a laminaset) on the basis of three attributes:
- planar vs. congruent shape of the laminae
- tabular vs. non-tabular shape of the lamina set
- horizontal or non-horizontal orientation of the laminae
Rather than doing that here, however, I will just show the four most common categories that would arise in such a classification (Figure \(\PageIndex{1}\)). What most workers consider planar lamination is the “planar; tabular set; \(\pm\) horizontal” variety in Figure \(\PageIndex{1}\). That is the focus of this chapter.
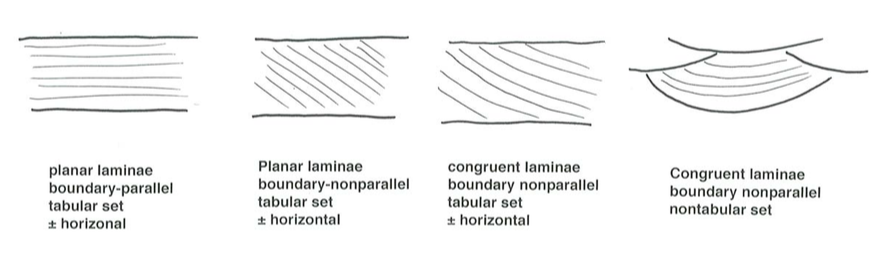
With regard to the three other items in Figure \(\PageIndex{1}\), most sedimentary geologists would call the laminae cross laminae, even though, according to the terminology I presented above, they would qualify as parallel (in the sense of congruent) laminae. I think most sedimentologists would agree that to a great extent such laminae owe their origin to processes that are specific to the lee regions of ripples or dunes: grain flows down angle-of-repose lee slopes; interleaving of grain-flow deposits and fallout deposits; and/or temporal variation in sediment supply to the lee region as a consequence of arrival of superimposed smaller bed forms to the brink region of the larger form.
In think that, similarly, most sedimentologists would agree that planar lamination in sands and sandstones is somehow associated with the existence of a planar transport surface, in what I called in Chapter 11 the upper-flow-regime plane bed, over which abundant sediment is being transported in traction. Planar lamination is also very common in muds, mudrocks, and shales, and it seems clear that much—probably most—such lamination is formed under conditions of weak currents by fallout without traction. The distinction is usually clear from the overall context of the deposit, aside from the contrast in particle size. After a few comments on the possibilities for paleoflow interpretations, and then a brief section on the characteristic features of planar lamination, the rest of the chapter deals with the origin of planar lamination in sands and in fine sediments.
In terms of paleoflow interpretation, in the spirit of Chapter 16, on cross stratification, we might take the approach of trying to identify the entire range of flow conditions under which the bed configuration is a plane bed rather than a bed covered with rugged bed forms—on the theory that planar lamination in sands is associated with plane-bed transport in the upper flow regime. This would, however, give us only a partial idea of how to interpret the environmental significance of planar-stratified beds. The problem is that, in contrast to cross- stratified beds, there are no obvious internal geometrical features that vary with flow and sediment conditions within that overall range, so we cannot try to go on to be more specific about environmental conditions, as we can with much success with cross-stratified beds. Moreover, there is no natural basis for deciding among interpretations involving unidirectional flows, oscillatory flows, or combined flows, all of which feature plane-bed transport in an upper flow regime.
Owing to these problems, the observational fodder for interpretation of planar lamination would have to lie in textural attributes like particle size distribution and particle orientation, or in subtle variations in lamina thickness and spatial continuity. There is an offsetting advantage, however: the scale of planar lamination is so small that its features can be studied in even small laboratory flumes.
Features of Planar Lamination
- Laminae range in thickness from just a few particle diameters to over a centimeter (in which case they should not technically be called laminae any more!), equivalent to as much as hundreds of particle diameters.
- The essential feature of planar laminae is that their extent is much greater than their thickness. At a minimum, the lateral extent is an order of magnitude greater than the thickness, and it can range up to many meters, which is at least three orders of magnitude grater than the thickness.
- Laminae, almost by definition, vary in their textural features (particle size, sorting, and shape); they are commonly graded, either normally or inversely.
- On parting surfaces through planar-laminated sandstones, parting lineation (also called, somewhat more precisely, parting-step lineation) is characteristic, presumably reflecting a tendency for flow-parallel orientation of slightly elongated particles under upper-flow-regime conditions.


