2.3: Some Dimensional Reasoning and its Consequences
- Page ID
- 4157
Obtaining the Correct Dimensions
Like every physically correct equation, Equation 2.2.1 must represent equality not only of magnitudes but also of dimensions. In most mechanical systems three basic dimensions are needed to express forces, motions, and system properties; these are usually taken to be mass (\(\mathrm{M}\)), length (\(\mathrm{L}\)), and time (\(\mathrm{T}\)). So whatever the form of the term or terms on the right side of Equation 2.2.1, the variables \(U\), \(D\), \(\rho\), and \(\mu\) must combine in such a way that each term has the dimensions of force, because the left side has the dimensions of force. The following list gives the dimensions of each of the five variables involved in flow past a sphere, in terms of mass \(\mathrm{M}\), length \(\mathrm{L}\), and time \(\mathrm{T}\):
\(\begin{array}{ll}{F_{D}} & {-\quad \mathrm{ML} / \mathrm{T}^{2}} \\ {U} & {-\quad\mathrm{L} / \mathrm{T}} \\ {D} & {-\quad\mathrm{L}} \\ {\rho} & {-\quad\mathrm{M} / \mathrm{L}^{3}} \\ {\mu} & {-\quad\mathrm{M} / \mathrm{LT}}\end{array}\)
The only variable here whose dimensions are not straightforward is \(\mu\); the dimensions \(\mathrm{M} / \mathrm{L} \mathrm{T}\) are obtained by use of Equation 1.3.6, by which \(\mu\) is defined.
It is advantageous to rewrite equations like Equation 2.2.1 in dimensionless form. To do this, first make the left side dimensionless by dividing \(F_{D}\) by some product of independent variables that itself has the dimensions of force. Using the list of dimensions above, you can verify that \(\rho U^{2} D^{2}\) has the dimensions of force:
\(\rho U^{2} D^{2}: \left(\mathrm{M} / \mathrm{L}^{3}\right)(\mathrm{L} / \mathrm{T})^{2}(\mathrm{L})^{2}=\mathrm{ML} / \mathrm{T}^{2}\)
So dividing the left side of Equation 2.2.1 by \(\rho U^{2} D^{2}\) makes the left side of the equation dimensionless. The result, \(F_{D} / \rho U^{2} D^{2}\), can be viewed as a dimensionless form of \(F_{D}\). That leaves the right side of Equation 2.2.1 to be made dimensionless. There is one and only one way the four variables \(U\), \(D\), \(\rho\), and \(\mu\) can be combined into a dimensionless variable, namely \(\rho U D / \mu\):
\(\rho U D / \mu\): \(\left(\mathrm{M} / \mathrm{L}^{3}\right)(\mathrm{L} / \mathrm{T})(\mathrm{L}) /(\mathrm{M} / \mathrm{LT})\) ... \(\mathrm{M}\), \(\mathrm{L}\), \(\mathrm{T}\) cancel
(That statement is not strictly true—but all the other possibilities are just \(\rho U D / \mu\) raised to some power, and they are not independent of \(\rho U D / \mu\).) So whatever the form of the function \(f\), the right side of the dimensionless form of Equation 2.2.1 can be written using just one dimensionless variable:
\[\frac{F_{D}}{\rho U^{2} D^{2}}=f\left(\frac{\rho U D}{\mu}\right) \label{dimensionless} \]
A Simplified Function
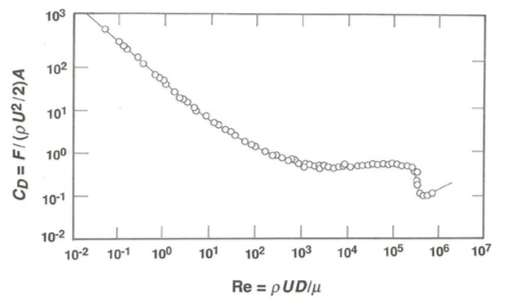
Equation \ref{dimensionless} is an equivalent but dimensionless form of Equation 2.2.1. The great advantage of the dimensionless equation is that it involves only two variables—a dependent dimensionless variable \(F_{D} / \rho U^{2} D^{2}\) and an independent dimensionless variable \(\rho U D / \mu\)—instead of the original five. Think of the enormous saving in effort this implies for an experimental program to characterize the drag force. If you had to measure \(F_{D}\) as a function of each one of the four variables while holding the other three constant, you would generate mountains of data and graphs. But Equation \ref{dimensionless} tells you that \(U\), \(D\), \(\rho\), and \(\mu\) need only be varied so as to make \(\rho U D / \mu\) vary. All of the experimental points for \(F_{D} / \rho U^{2} D^{2}\) obtained by varying \(\rho U D / \mu\) should plot as a curve in a two- dimensional graph with these two variables along the axes. Whatever the values of \(U\), \(D\), \(\rho\), and \(\mu\), all possible realizations of flow past a sphere are expressed by just one curve. This curve is shown in Figure \(\PageIndex{1}\) together with some of the experimental points that have been used to define it. The physics behind the curve is discussed in Chapter 3, after more background in the principles of fluid dynamics. And you could find the curve by varying only one of the four variables \(U\), \(D\), \(\rho\), and \(\mu\)—although you may not be able to get a very wide range of values of \(\rho U D / \mu\) by varying only one of those variables. A fairly small number of experiments involving values of the original independent variables that combined to span a wide range of \(\rho U D / \mu\) would suffice to characterize all other possible combinations of independent variables. This is because each point in the dimensionless graph represents a great many different possible combinations of the original variables—an infinity of these, in fact. You thus gain a far-reaching predictive capability on the basis of relatively little observational effort.
A skeptic might find all this to be too good to be true. But the fact is that this is how things work, and the analysis of flow past a sphere is just one good example. A note of caution is in order, however. It is prudent to vary as many of the variables over as wide a range as possible; this does not take an enormous number of observations, and it is a check on the correctness of your analysis. You will see below in more detail that if there is a larger number of important variables than you think, your data points would form a scattered band rather than a single curve. Then if you varied just one variable to try to find the curve, you would indeed get a curve, but it would not be the curve you were after; you would be missing the scatter that would manifest itself if you varied the other variables as well.
Several notes
First, variables of the form \(\rho U D / \mu\) are called Reynolds numbers, usually denoted by \(\mathrm{Re}\). Whenever both density and viscosity are important in a problem and both a length variable and a velocity are involved, a Reynolds number can be formed and used. There are thus many different Reynolds numbers, with different length and velocity variables depending on the particular problem. You will encounter others in later chapters.
Second, for the steady flow we have assumed, the variables \(U\), \(D\), \(\rho\), and \(\mu\) characterize not only everything about the distributions of shear stress and pressure over the entire surface of the sphere, which add up to \(F_{D}\), but also the distributions of shear stress, pressure, and fluid velocity at every point in the surrounding fluid. Because \(\rho U D / \mu\) replaces these four variables on the right side of Equation \ref{dimensionless}, the same can be said of the Reynolds number. Anything about forces and motions you might want to consider can be viewed as being specified completely by the Reynolds number.
Third, there is a further important consequence of the fact that each point on the curve of \(F_{D} / \rho U^{2} D^{2}\) vs. \(\rho U D / \mu\) represents an infinity of combinations of \(U\), \(D\), \(\rho\), and \(\mu\). Suppose that you wanted to find the drag force exerted by a certain flow on a sphere that is too large to fit into your laboratory or your basement. You could work with a much smaller sphere by adjusting the values of \(U\), \(\rho\), and \(\mu\) so that \(\rho U D / \mu\) is the same as in the flow in question past the large sphere (Figure \(\PageIndex{2}\)). Then from the curve in Figure \(\PageIndex{1}\) the value of \(F_{D} / \rho U^{2} D^{2}\) is also the same, and from it you could find the drag force \(F_{D}\) on the large sphere by substituting the corresponding values of \(U\), \(D\), and \(\rho\). Or, on the other hand, you could study the flow around a very small sphere by use of a much larger sphere, with the same complete confidence in the results (Figure \(\PageIndex{2}\)). This is the essence of scale modeling: the study of one physical system by use of another at a smaller or larger physical scale but with variables adjusted so that all forces and motions in the two systems are in the same proportions. Figure \(\PageIndex{2}\) shows how you might use flow around a small sphere with diameter \(D_{m}\) to model flow around a much larger sphere with diameter \(D_{o}\). You would have to adjust the flow velocities \(U_{m}\) and \(U_{o}\), as well as the fluid viscosities \(\mu_{m}\) and \(\mu_{o}\) and the fluid densities \(\rho_{m}\) and \(\rho_{o}\), so that the Reynolds number \(\mathrm{Re}_{m}\), equal to \(\rho_{m} U_{m} D_{m} / \mu_{m}\), in the model is the same as the Reynolds number \(\mathrm{Re}_{o}\), equal to \(\rho_{o} U_{o} D_{o} / \mu_{o}\), in the large-scale flow. Then all forces and motions are in the same proportion in the two flows, and, specifically, the dimensionless drag force, or the drag coefficient, is the same in the two flows. Despite the great difference in physical scale, both of the flows are represented by the same point on the graph of drag coefficient vs. Reynolds number, so anything about the two flows, provided only that it is expressed in dimensionless form, is the same in the two flows. Each point on the curve of \(F_{D} / \rho U^{2} D^{2}\) vs. \(\rho U D / \mu\) represents an infinite number of possible experiments, each of which is a scale model of all the others!

Fourth, in Figure \(\PageIndex{1}\) the dimensionless drag force is written in a conventional form that is slightly different from that derived above: \(F_{D} /\left(\rho U^{2} / 2\right) A\), where \(A\) is the cross-sectional area of the sphere, equal to \(\pi D^{2} / 4\). This differs from \(F_{D} / \rho U^{2} D^{2}\) by the factor \(\pi / 8\), but its dimensions are exactly the same. It is usually called a drag coefficient, denoted by \(C_{D}\); you can see why that term came about by writing
\[F_{D}=C_{D} \frac{\rho U^{2}}{2} A \label{2.3} \]
where the factor \(\left(\rho U^{2} / 2\right) A\) on the right side has dimensions of force. The functional relationship between dimensionless drag force and Reynolds number in Equation \ref{dimensionless} can be written in an entirely equivalent form using \(C_{D}\):
\[C_{D}=\frac{F D}{\frac{\rho U^{2}}{2} A}=f\left(\frac{\rho U D}{\mu}\right) \label{2.4} \]
Fifth, there are alternative versions of the dependent dimensionless variable. Dividing by \(\rho U^{2} D^{2}\) is not the only way to nondimensionalize \(F_{D}\). You can check for yourself that \(F_{D} / \mu U D\), \(\rho F_{D} / \mu^{2}\), and \(F_{D} / \mu U\) are other possibilities, obtained by combining \(F_{D}\) with the four variables \(\rho\), \(\mu\), \(U\), and \(D\) taken three at a time. (You will see in the next section how to derive such variables.) Sometimes, as in the last two cases, one of the variables drops out; this happens when \(\mathrm{M}\) or \(\mathrm{L}\) or \(\mathrm{T}\) appears in only one of the four variables chosen. Any of these three alternative dependent dimensionless variables would serve just as well as \(F_{D} / \rho U^{2} D^{2}\) to represent the data. You will see below, however, that sometimes one is more revealing than the others.


