2.2: Which Variables are Important?
- Page ID
- 4156
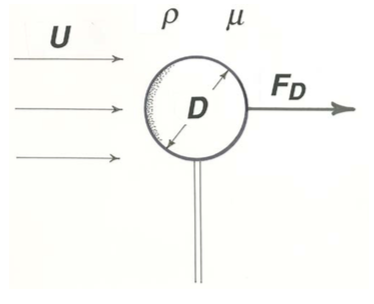
Think first about the resultant drag force \(F_{D}\) exerted on the sphere by the fluid (Figure \(\PageIndex{1}\)). To account fully for the value assumed by \(F_{D}\) for a given sphere in a given fluid, we have to specify the values of certain other variables. (This carefully phrased sentence should not be interpreted as implying that \(F_{D}\) is necessarily the “dependent variable” in the problem; for a sphere settling under its own weight, it is more natural to think of \(F_{D}\) as an independent variable and settling velocity as the dependent variable. What is important here is that there is a one-to-one correspondence between the values of \(F_{D}\) and the values of those other variables, irrespective of their dependence or independence. That said, however, for convenience I will refer to such variables as independent variables.)
- The velocity \(U\) of the sphere relative to the fluid is important because it affects the shear in the fluid near the surface of the sphere, and therefore by Equation 1.3.7 the shear stress.
- Sphere diameter \(D\) is important for the same reason.
- Viscosity \(\mu\) is important because it determines the shear force associated with a given rate of shear.
- Fluid density \(\rho\) must also be included, because the forces associated with the accelerations in the fluid depend upon \(\rho\): the response of a body to a force exerted on it depends on the mass of the body; that is the essence of Newton’s second law. If the sphere is in steady motion far from solid walls or a free surface, you can assume that no other variables are important.
So
\[F_{D}=f(U, D, \rho, \mu) \label{dragforce} \]
where \(f\) is some function with one or more terms involving the four independent variables (Figure \(\PageIndex{1}\)). (I will often use the same symbol \(f\) for unrelated functions. In Chapter 4, \(f\) is also used for a quantity called the friction factor.)
You might reasonably ask why neither sphere density nor acceleration of gravity are on the list. These are relevant only if the sphere settles under its own weight, and then only because they determine the weight of the sphere, to which \(F_{D}\) is then equal after a steady state of settling is attained. Variables that enter the problem only by their effect on other variables already on the list and not because of some separate effect need not be included in the analysis. And there is no reason to think that either of these has any such significance.
If we are lucky in problems like this, we can use theory to derive an analytical form for the function in Equation \ref{dragforce} that agrees well with observation. If not, we have to attempt a numerical solution or rely solely on experiment. For flow past a sphere there is indeed an analytical solution, described later in this chapter, that agrees beautifully with experimental data, but it holds over only a limited range of the independent variables; over the rest of the range we can obtain the function by experiment, as is commonly the case in problems of flow of real fluids. With flow past the sphere as an example we need to consider how we can best go about organizing both data and thought by resorting to dimensional reasoning.


