5.2: Two Practical Problems
- Page ID
- 4177
One of the interesting things about open-channel flow is the effect of gravity on the shape of the free surface relative to the solid boundary. Babbling brooks and white-water rivers clearly have complex free-surface geometries governed by bed relief, expansions and contractions of the channel, and, less obviously, upstream and downstream conditions. But all open-channel flow, even broad, majestic rivers like the Mississippi, or flows in laboratory channels we try to keep as nearly uniform as possible, are subject to such effects of gravity. To make this effect concrete, I will pose two questions at this point for you to think about. Both are of great practical importance to engineers dealing with open- channel flows.
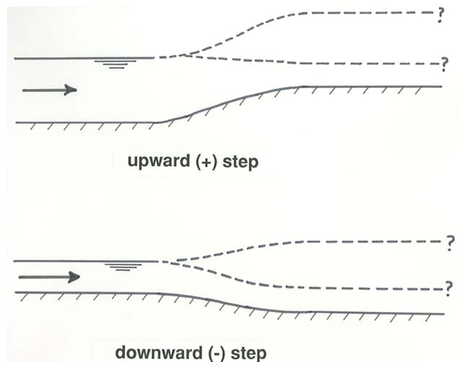
Your intuition might have some trouble with the first question. Suppose that you set up a nice open-channel flow, in a wide rectangular channel, just for the sake of definiteness, with a planar bottom, which may or may not be sloping. Then, at a particular position down along the channel you introduce a smooth and gentle step in the channel bottom, either upward or downward (Figure \(\PageIndex{1}\)). The question is: does the water surface rise or fall over the step, relative to its upstream level?
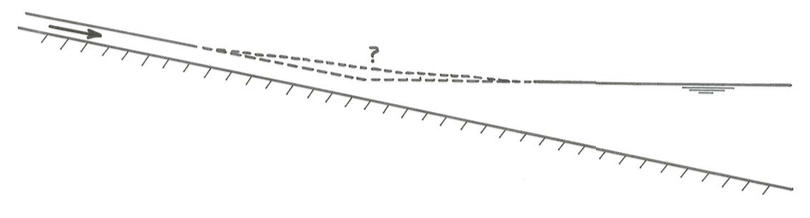
You will probably feel more comfortable with the second question. A river with a constant bottom slope is dammed at a certain point, so that the river has to merge somehow into a deep reservoir formed in the river valley (Figure \(\PageIndex{2}\)). You can assume that far upstream in the channel the flow is very nearly uniform. That sloping water surface upstream has to pass continuously into the horizontal water surface of the reservoir, where the water velocity is negligible. What would the water-surface profile look like along a streamwise vertical cross section through the channel and the reservoir? Would it change very gradually, all the while sloping monotonically down toward the reservoir? Or would it continue unchanged all the way to the reservoir level, to meet the water surface in the reservoir by an abrupt change in water-surface slope?
Before attacking these problems, you need a brief look at uniform flow, which is a useful reference for study of the nonuniformities introduced by the joint effect of gravity and the changing boundary geometry. Then I will have to expose you to more material on flow energy, because it turns out that this is the key to the problems posed above.


