8.2: Winds and the Coriolis Effect
- Page ID
- 4511
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
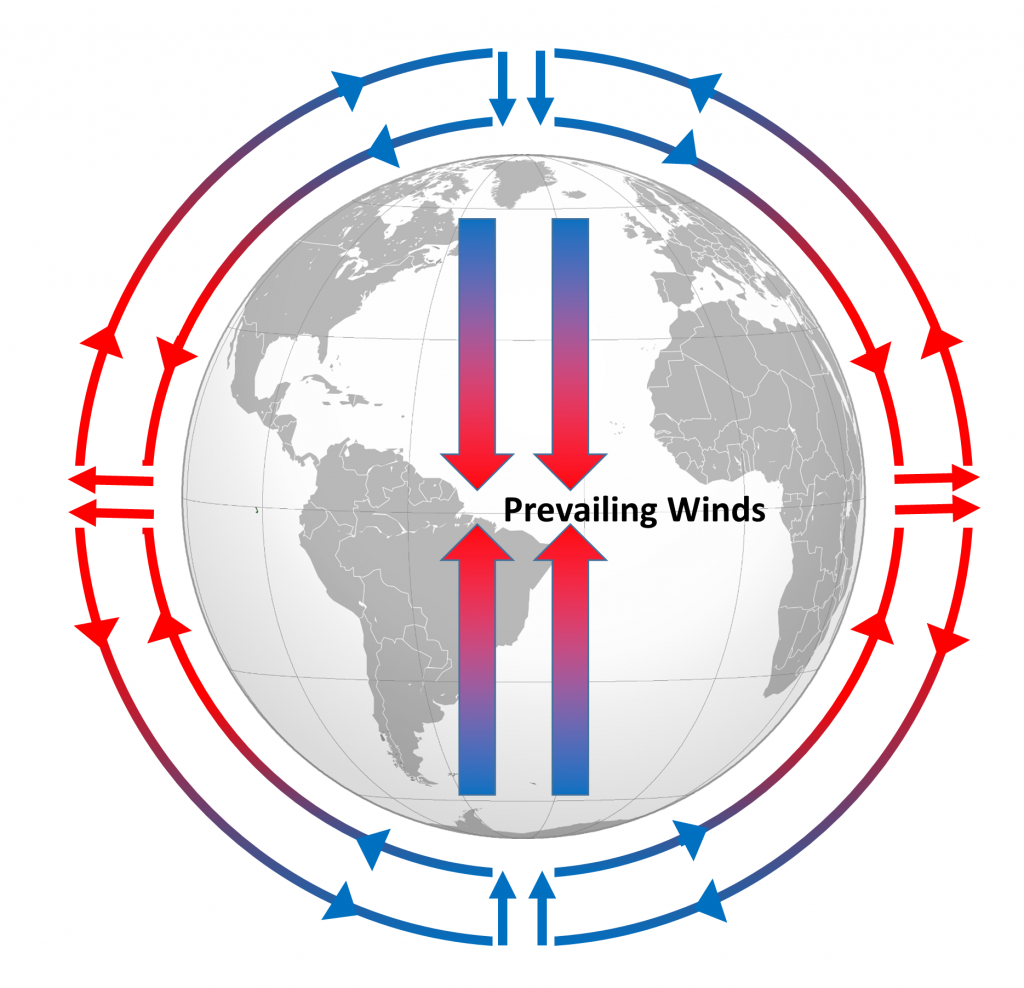
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Differential heating of the Earth’s surface results in equatorial regions receiving more heat than the poles (section 8.1). As air is warmed at the equator it becomes less dense and rises, while at the poles the cold air is denser and sinks. If the Earth was non-rotating, the warm air rising at the equator would reach the upper atmosphere and begin moving horizontally towards the poles. As the air reached the poles it would cool and sink, and would move over the surface of Earth back towards the equator. This would result in one large atmospheric convection cell in each hemisphere (Figure \(\PageIndex{1}\)), with air rising at the equator and sinking at the poles, and the movement of air over the Earth’s surface creating the winds. On this non-rotating Earth, the prevailing winds would thus blow from the poles towards the equator in both hemispheres (Figure \(\PageIndex{1}\)).
The non-rotating situation in Figure \(\PageIndex{1}\) is of course only hypothetical, and in reality the Earth’s rotation makes this atmospheric circulation a bit more complex. The paths of the winds on a rotating Earth are deflected by the Coriolis Effect. The Coriolis Effect is a result of the fact that different latitudes on Earth rotate at different speeds. This is because every point on Earth must make a complete rotation in 24 hours, but some points must travel farther, and therefore faster, to complete the rotation in the same amount of time. In 24 hours a point on the equator must complete a rotation distance equal to the circumference of the Earth, which is about 40,000 km. A point right on the poles covers no distance in that time; it just turns in a circle. So the speed of rotation at the equator is about 1600 km/hr, while at the poles the speed is 0 km/hr. Latitudes in between rotate at intermediate speeds; approximately 1400 km/hr at 30o and 800 km/hr at 60o. As objects move over the surface of the Earth they encounter regions of varying speed, which causes their path to be deflected by the Coriolis Effect.
To explain the Coriolis Effect, imagine a cannon positioned at the equator and facing north. Even though the cannon appears stationary to someone on Earth, it is in fact moving east at about 1600 km/hr due to Earth’s rotation. When the cannon fires the projectile travels north towards its target; but it also continues to move to the east at 1600 km/hr, the speed it had while it was still in the cannon. As the shell moves over higher latitudes, its momentum carries it eastward faster than the speed at which the ground beneath it is rotating. For example, by 30o latitude the shell is moving east at 1600 km/hr while the ground is moving east at only 1400 km/hr. Therefore, the shell gets “ahead” of its target, and will land to the east of its intended destination. From the point of view of the cannon, the path of the projectile appears to have been deflected to the right (red arrow, Figure \(\PageIndex{2}\)). Similarly, a cannon located at 60o and facing the equator will be moving east at 800 km/hr. When its shell is fired towards the equator, the shell will be moving east at 800 km/hr, but as it approaches the equator it will be moving over land that is traveling east faster than the projectile. So the projectile gets “behind” its target, and will land to the west of its destination. But from the point of view of the cannon facing the equator, the path of the shell still appears to have been deflected to the right (green arrow, Figure \(\PageIndex{2}\)). Therefore, in the Northern Hemisphere, the apparent Coriolis deflection will always be to the right.
In the Southern Hemisphere the situation is reversed (Figure \(\PageIndex{2}\)). Objects moving towards the equator from the south pole are moving from low speed to high speed, so are left behind and their path is deflected to the left. Movement from the equator towards the south pole also leads to deflection to the left. In the Southern Hemisphere, the Coriolis deflection is always to the left from the point of origin.
The magnitude of the Coriolis deflection is related to the difference in rotation speed between the start and end points. Between the poles and 60o latitude, the difference in rotation speed is 800 km/hr. Between the equator and 30o latitude, the difference is only 200 km/hr (Figure \(\PageIndex{2}\)). Therefore the strength of the Coriolis Effect is stronger near the poles, and weaker at the equator.

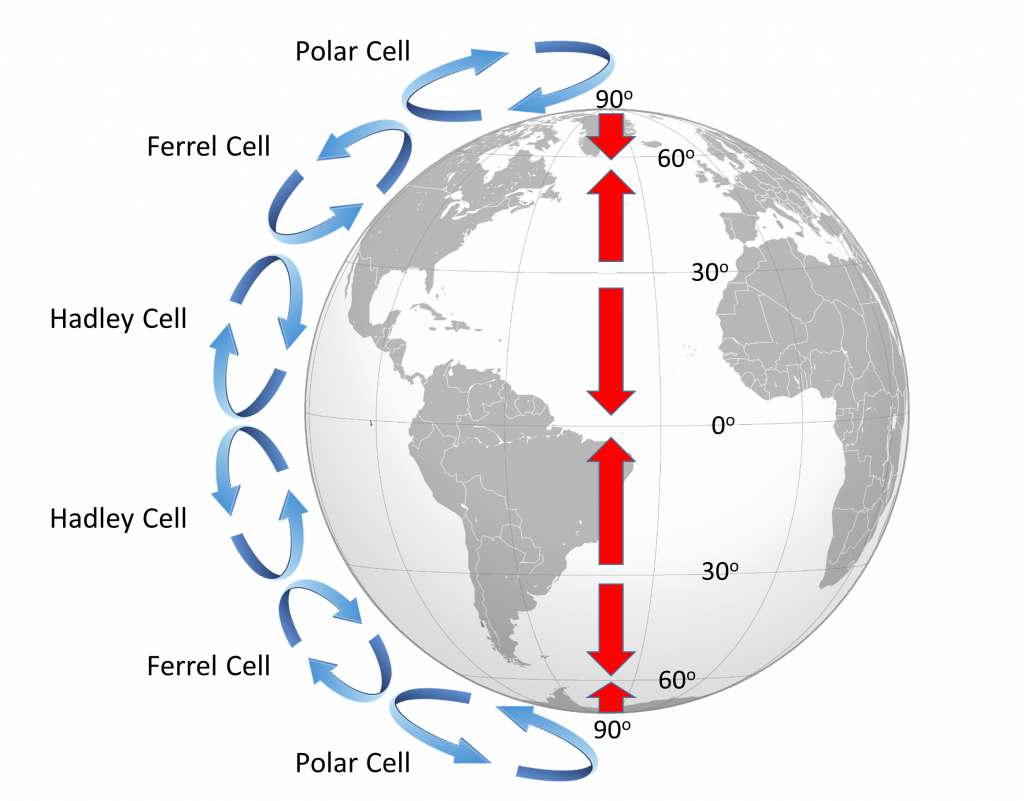
Because of the rotation of the Earth and the Coriolis Effect, rather than a single atmospheric convection cell in each hemisphere, there are three major cells per hemisphere. Warm air rising at the equator cools as it moves through the upper atmosphere, and it descends at around 30o latitude. The convection cells created by rising air at the equator and sinking air at 30o are referred to as Hadley Cells, of which there is one in each hemisphere. The cold air that descends at the poles moves over the Earth’s surface towards the equator, and by about 60o latitude it begins to rise, creating a Polar Cell between 60o and 90o. Between 30o and 60o lie the Ferrel Cells, composed of sinking air at 30o and rising air at 60o (Figure \(\PageIndex{3}\)). With three convection cells in each hemisphere that rotate in alternate directions, the surface winds no longer always blow from the poles towards the equator as in the non-rotating Earth in Figure \(\PageIndex{1}\). Instead, surface winds in both hemispheres blow towards the equator between 90o and 60o latitude, and between 0o and 30o latitude. Between 30o and 60o latitude, the surface winds blow towards the poles (Figure \(\PageIndex{3}\)).
The surface winds created by the atmospheric convection cells are also influenced by the Coriolis Effect as they change latitudes. The Coriolis Effect deflects the path of the winds to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. Adding this deflection leads to the pattern of prevailing winds illustrated in Figure \(\PageIndex{4}\). Between the equator and 30o latitude are the trade winds; the northeast trade winds in the Northern Hemisphere and the southeast trade winds in the Southern Hemisphere (note that winds are named based on the direction from which they originate, not where they are going). The westerlies are the dominant winds between 30o and 60o in both hemispheres, and the polar easterlies are found between 60o and the poles.
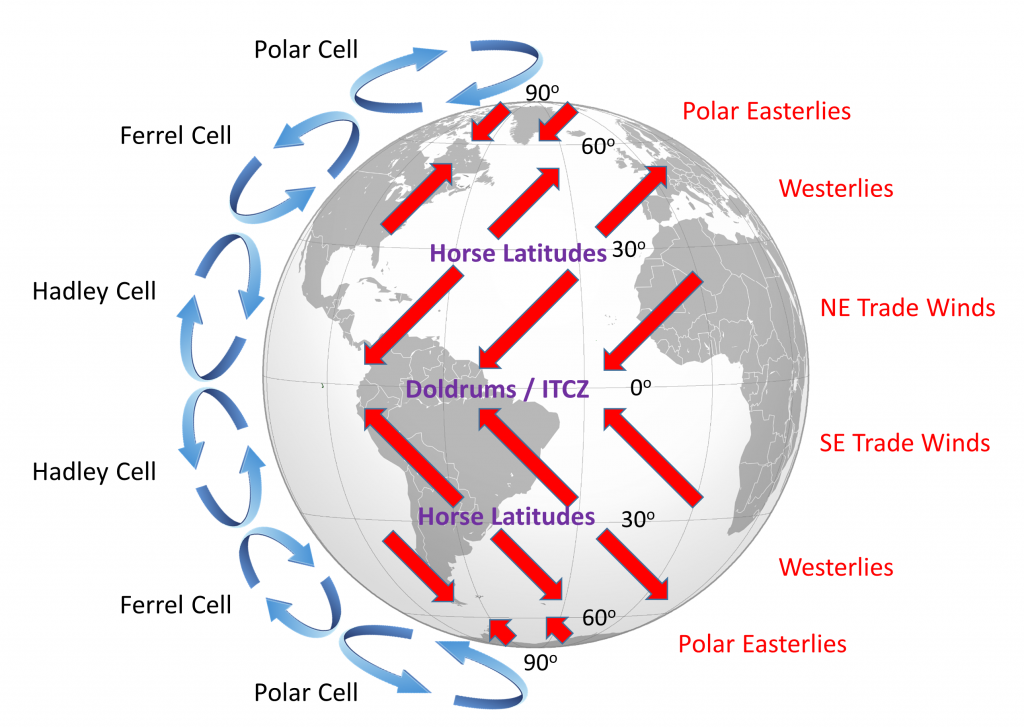
In between these wind bands lie regions of high and low pressure. High pressure zones occur where air is descending, while low pressure zones indicate rising air. Along the equator the rising air creates a low pressure region called the doldrums, or the Intertropical Convergence Zone (ITCZ)(convergence zone because this is where the trade winds converge). At 30o latitude there are high pressure zones of descending air known as the horse latitudes, or the subtropical highs. Finally, at 60o lies another low pressure region called the polar front. It should be noted that these high and low pressure zones are not fixed in place; their latitude fluctuates depending on the season, and these fluctuations have important implications for regional climates.
Doldrums? Horse latitudes? Trade winds?
These may seem like some odd names for these atmospheric phenomena, but many of them can be traced back to maritime traditions and lore.
The doldrums refer to regions of low pressure around the equator. In these areas, air is rising rather than moving horizontally, so these regions commonly encounter very light winds. The lack of wind could leave sailing ships becalmed for days or weeks at a time, which was not good for the morale of the ship’s crew.
Like the doldrums the horse latitudes are also areas with light winds, this time due to descending air, which could leave ships becalmed. One explanation for the term “horse latitudes” is that when these ships became stranded they ran the risk of running out of food or water. To conserve these resources, sailors would throw their dead or dying horses overboard, hence the “horse latitudes.” Another explanation is that many sailors received part of their pay before a voyage, and often spent it before departing. This meant that they would spend the first part of the voyage working without pay and in debt, a period called the “dead horse” time, which might last for a few months. When they started earning their pay once again, they had a “dead horse” ceremony and threw a pretend horse overboard. The timing of this ceremony often coincided with reaching the horse latitudes, leading to the association of the ceremony with the location. A third explanation is that a ship was referred to as “horsed” when winds were weak and the ship instead had to rely on ocean currents to move them. This could be a common occurrence in the high pressure zones around 30o latitude, so they were referred to as the horse latitudes.
The term trade winds may have originally derived from the terms for “track” or “path”, but the term may have become more common during European exploration and commercialization of the New World. Mariners sailing from Europe to the New World could sail south until they reached the trade winds, which would then propel their ships across the Atlantic to the Caribbean. To return to Europe, ships could sail to the northeast until they entered the westerlies, which would then steer them back to Europe.


