3: The Coriolis Force

The Coriolis force is a central element of the dynamics of ocean and atmosphere flows. A rigorous derivation using vector calculus is given in many textbooks on classical mechanics, but such derivations are often not the most effective way to obtain a conceptual understanding. Therefore, we will provide a more intuitive qualitative explanation here. Throughout this chapter about Geophysical Flows, we have been talking a lot about Newton's 2nd law, but the key to understanding the Coriolis force is rather Newton's 1st law: an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. The Earth and everything on it is constantly moving, as the Earth rotates around its axis. Moreover, the direction of all this movement changes constantly: while you are typing at your desk at 2 p.m., you are moving in the exact opposite direction compared to when you were lying in your bed at 2 a.m. These forced changes in the direction of the movement of objects that tend to keep moving in the same direction is what gives rise to so-called pseudo-forces (which are actually very real, if you happen to live on a rotating planet such as the Earth).

The pseudo-force that is the easiest to understand conceptually is the centrifugal force, depicted below.

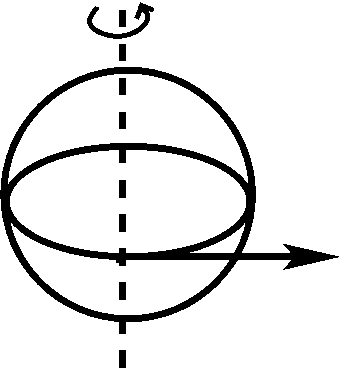
Essentially, objects tend to be thrown off a rotating body, because the objects keep moving in a straight line (as indicated by the arrow), while the surface of the rotating body does not move in a straight line (as indicated by the circle). Fortunately, we don't need to worry about being thrown off the Earth, because the gravitational force that keeps our feet on the ground is about 300 times stronger than the centrifugal force. The centrifugal force plays no significant role in the dynamics of the ocean and the atmosphere, but it does make the Earth slightly elliptical.

The Coriolis force is a pseudo-force that emerges when an object is moving on the surface of a rotating body. The Coriolis force is conceptually much more subtle than the centrifugal force and, in fact, consists of two different effects, each illustrated below:

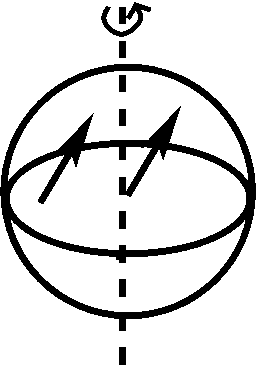
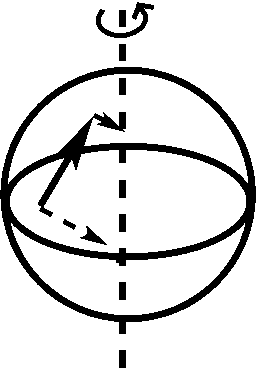
The left panel illustrates the first effect: an object that keeps moving in the same direction in absolute space appears to change direction, as the Earth turns to the right. At first, the object moves straight North toward the pole (left arrow), but then, the direction of the movement becomes Northeast in the Earth frame of reference (right arrow), even though the direction and speed of the object have not changed in absolute space. The right panel illustrates the second effect: as an object moves on the Earth's surface (as indicated by the solid arrow), it carries the velocity of the Earth rotation (dashed arrows) with it. As the object moves North, it comes into regions where the velocity of the Earth rotation is smaller than at its original location. Thus, it will have an excess velocity to the East which deflects the movement from the North toward the Northeast, when viewed in the Earth frame of reference. In the Earth frame of reference, each of these 2 effects leads to an acceleration with a magnitude equal to \(\Omega * v \sin\theta \) (with \(\Omega \) the angular velocity of the Earth, \(v\) the velocity of the object in the Earth frame of reference, and \(\theta\) the latitude), so the total acceleration adds up to \(2 * \Omega * v \sin\theta\) or \(f * v\), with the Coriolis parameter \(f = 2 * \Omega * \sin\theta\). The Coriolis force is at a \(90^{\circ}\) angle with respect to the movement of the object, to the right in the Northern hemisphere, to the left in the Southern Hemisphere; it vanishes at the Equator (\(\theta=0\)). In the zonal and meridional directions, the accelerations amount to:

\[\dfrac{du}{dt}=f * v \]

\[\dfrac{dv}{dt}=-f * u\]

The impact of the Coriolis force on moving parcels of air (or water) is demonstrated here.