6.8.2: Critical shear stress and settling velocity

Sand, silt and clay particles are continuously entrained, transported and deposited in the coastal system by currents and waves. Due to the difference in grain size and cohesiveness, the sediment transport characteristics of sand and mud are different. In general, sand is transported as bed load (at the bed-water interface) and as suspended load (higher in the water column). For low sediment concentrations, silt and clay are only transported in suspension. For high concentrations, silt and clay can also be transported as fluid mud in a layer near the bed. In that case, the fluid mud will act as a viscous layer on top of the bed, blocking exchange of sand between the bed and the water column.

We have seen that the fall velocity is an important parameter determining the vertical distribution of suspended sediment (see for instance Eq. 6.6.3.1). The fall velocity depends on the size, shape and specific density of the particles and of the water temperature and the sediment concentration. As a reference, an individual silt particle of \(10\ \mu m\) has a fall velocity in still water of about \(0.1\ mm/s\). For sand, the particle properties are relatively independent of time (because the quartz crystals are chemically hard and stable, it takes years to change the size of a sand grain). But, as we have seen in Sect. 2.6.2, the size and shape of mud can change quite easily. As a result of flocculation, the size of individual mud particles increases. With this increase, particles become heavier, which will speed up the settling of the particles. On the other hand, due to the increase in size, also the drag force, the resistance the particle ‘feels’ when settling, will increase. This will slow down the particle and can eventually cause deflocculation.

Figure 6.17: Effect of mud content on the critical erosion shear stress for two different sand-mud mixtures (data from Torfs, 1995). Mud content on horizontal axis represents % fines smaller than \(63\ \mu m\), hence including silt and clay fractions.

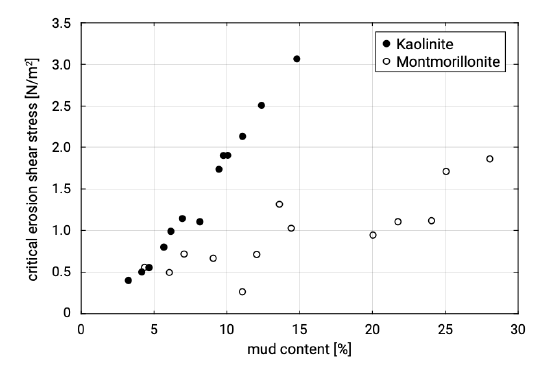
Another factor influencing the sediment transport is the exchange between the bottom layer and the water column. The upward sediment flux from the bed into the water column strongly depends on the bed composition. From laboratory experiments it was concluded that two regimes can be distinguished: a non-cohesive and a cohesive regime (Van Ledden & Wang, 2001). The clay content (the weight percentage of particles with a grain size smaller than \(4\ \mu m\)) of the bed material is the governing parameter for the transition between both regimes. For clay content of less than 5% to 10% the bed behaves more or less non-cohesively. Sand and mud are eroded more or less independently, so the ‘normal’ formulations for the bed erosion can be used. For clay content exceeding 5% to 10% the bed behaves cohesively. The sand and mud particles are eroded simultaneously. Figure 6.17 gives the critical velocities as a function of mud (clay and silt) content in the bottom material.

In sediment transport modelling, the exchange processes between water column and bottom layer are often assumed to be governed by the critical bed shear stress of the bottom material and the actual occurring bed shear stresses (Sect. 6.3).

For actual bed shear stresses larger than the critical bed shear stress of the bed material, the grains can be eroded, whereas for actual bed shear stresses smaller than the critical bed shear stress of the bed material, the grains can settle:

\[\tau_{b, \text{actual}} > \tau_{b, cr} \to \text{erosion}\]

\[\tau_{b, \text{actual}} < \tau_{b, cr} \to \text{sedimentation}\]

For non-cohesive material the critical bed shear stress \(\tau_{b, cr}\) for erosion is equal to the critical bed shear stress for sedimentation. For cohesive material, where there is a strong binding force between the particles, this is not the case. The critical bed shear stress for erosion is larger than the critical bed shear stress for sedimentation. This implies that for a range of actual bed shear stresses, there is no exchange with the bottom layer in the case of cohesive sediments:

\[\tau_{b, \text{actual}} > \tau_{b, cr, er} \ \ \ \ \to \text{erosion}\]

\[\tau_{b, cr, sed} < \tau_{b, \text{actual}} < \tau_{b, cr, er} \ \ \to \text{no exchange with bottom layer}\]

\[\tau_{b, \text{actual}} < \tau_{b, cr, sed}\ \ \ \ \to \text{sedimentation}\]

The exact formulations for sediment transport of mixtures of sand and mud are still a subject of research.