6.4.2: Practical modelling of sediment transport
- Page ID
- 16350
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The mechanisms behind bed load and suspended load are quite different. It is there- fore common practice to use separate transport formulations for the two modes of transport.
Bed load transport is almost exclusively determined by the bed shear stress acting on the sediment particles that roll, slide and jump along the bed. Hence, bed load formulations are often expressed in terms of bed-shear stress due to currents and waves, often supplemented with a criterion that describes initiation of motion. These formulations are based on either a time-averaged or an instantaneous bed shear stress (Sect. 6.5). In the latter case the sediment is normally assumed to respond instantaneously (without delay) to the intra-wave (within the wave-period) shear stress variation. This is a so-called quasi-steady approach to bed load transport. It assumes that inertia (resistance to accelerations and decelerations) plays a minor role only. This is probably a valid assumption for particles smaller than a few millimetres. Generally, the coefficients in the formulas are empirically derived. In practical applications, bed load transport formulas are assumed to predict sheet-flow transport rates when used for large Shields parameters.
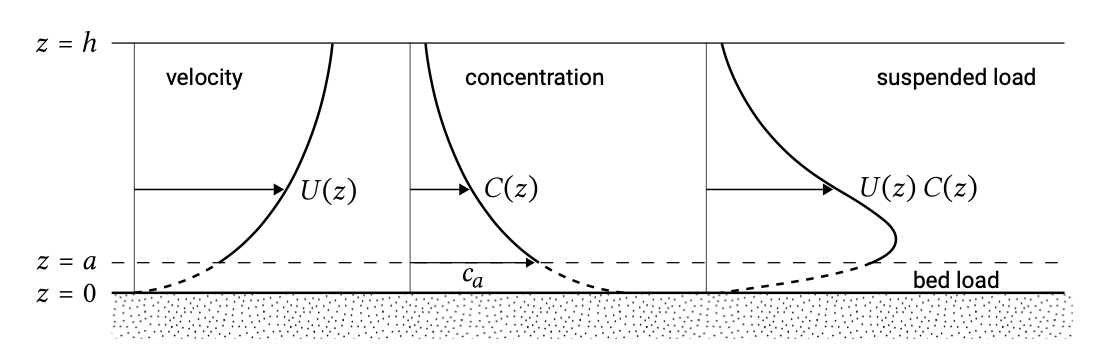
Suspended load transport takes place above the bed load layer. This is depicted in Fig. 6.10. The suspended sediment flux at a certain height above the bed is often modelled as the product of the sediment concentration \(c\) and the horizontal velocity \(u\) of the water that is transporting the sediment. The suspended sediment transport can be computed by integrating the suspended sediment flux \(uc\) from the top of the bed load layer to the water level. In order to compute the sediment concentration \(c\) it is generally assumed that turbulent diffusive forces are responsible for transporting the sediment upwards in the water column against the downward movement with the fall velocity. This approach is treated in detail in Sect. 6.6.
Since sediment particles are allowed time to settle, suspended load does not respond instantaneously to the hydrodynamic conditions. At the top of the bed load layer a boundary condition needs to be supplied, for instance a prescribed concentration at \(z = a\) (called reference concentration) or a prescribed pick-up rate from the bed. Since the bed load transport is determined by the excess shear stress (above a critical value), the reference concentration should be a function of this as well. The exact distinction between the bed load and suspended load is quite arbitrary.
In the coastal zone, where waves play an important role in the water motion, both the water velocity \(u\) and the sediment concentration \(c\), usually vary strongly as a function of time, on a scale comparable to the wave period. However, in engineering applications often only the wave-averaged velocity distribution \(U(z)\) and wave averaged concentration \(C(z)\) are used (as shown in Fig. 6.10). The validity of this approach is discussed later.
As mentioned before, the diffusion approach to suspended load transport only makes real sense in the case of a plane bed. In the case of a rippled bed, vortices shed off the rippled bed bring sediment into suspension. This is an organised rather than a turbulent motion. In practical situations, the presence of ripples can be taken into account by a larger pick-up rate and diffusivity of sediment (Sect. 6.6).
An entirely different approach to bed load and suspended sediment transport is the energetics approach (Bagnold, 1962, 1963, 1966; Bailard, 1981; Bailard & Inman, 1981; Bowen, 1980). It assumes that a certain portion of the fluid energy is expended to keep the sediment, in both bed load and suspended load, in motion. This results in quasi-steady formulations that relate the bed load and suspended load transport to the instantaneous intra-wave velocity at a certain height above the bed. The energetics approach will be treated in Sect. 6.7.
The sum of the bed load transport rate \(S_b\) and suspended transport rate \(S_s\) equals the total transport rate \(S_t\):
\[S_t = S_b + S_s\]
Here \(S_b\) and \(S_t\) can denote the instantaneous or averaged (over sufficient wave periods) sediment transport. Instead of separately modelling bed load and suspended load transport, sometimes a total load formula is used that is assumed to predict the total transport. Such a total load formula could for instance be a function of the time-averaged bed shear stress.


