12.1.3: X-ray Patterns, Symmetry and Mineral Identification

Last updated
Save as PDF

Page ID: 18384

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

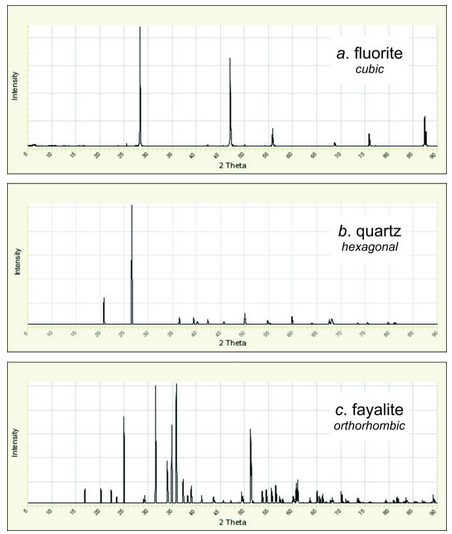
12.27.jpg — Figure 12.27: Diffraction patterns and symmetry

Different minerals produce different diffraction patterns because patterns depend on mineral composition and on the locations of atoms in unit cells. So, space symmetry, which relates to atom location, has great influence on diffraction patterns. Crystals with high symmetry contain identical planes of atoms in multiple directions. Consequently, fewer d-values cause diffraction – there are fewer diffraction peaks – than for crystals with low symmetry. And for crystals with high symmetry, X-ray peaks may seem somewhat regularly spaced on diffractograms. In contrast, low crystal symmetry means diffraction occurs in many more directions and diffraction patterns are irregular.

Figure 12.27 shows diffraction patterns for fluorite, quartz, and fayalite. Fluorite is cubic, quartz is hexagonal, and fayalite is orthorhombic. So, crystal symmetry increases downward in the figure. The number of reflections increases from fluorite to quartz to fayalite, and the patterns for fluorite and quartz appear to have a more even spacing of peaks.

An experienced crystallographer can often tell the crystal system with one look at a diffraction pattern, even if they do not know what the mineral is. This is most easily done for high-symmetry systems (such as cubic, hexagonal, or orthorhombic) and may be impossible for monoclinic or triclinic patterns. Experienced crystallographers also learn to identify common minerals quickly. Quartz, for example, has a strong peak at 20.8^o 2θ, a stronger peak at 26.6^o, and no other significant reflections (Figure 12.27b). That is enough to identify it. Graphite also has few peaks with its strongest at about 26.7^o, but it lacks a peak near 20.8^o. Calcite has a very strong peak just below 30^o. And many other minerals have specific peaks that crystallographers quickly spot.

12.28.png — Figure 12.28: Diffraction pattern for phlogopite

Even if we cannot identify a mineral with a quick look, we can sometimes figure out the general kind of mineral that was X-rayed. For example, many minerals have no X-ray peaks below 20^o 2θ, and most minerals have no peaks below 10^o. But clay minerals have broad peaks in the 5^o to 7^o range, and phlogopite and other micas have very large peaks at around 9^o 2θ. Figure 12.28 shows an example pattern for phlogopite, a mica; the strongest peak is at 8.7^o. Diffraction patterns for amphiboles, too, have a distinguishing characteristic – a double peak at 10-11^o 2θ characterizes tremolite and most other amphiboles. Figure 12.28b shows a typical diffraction pattern for an amphibole.

The low-angle reflections produced by clays and micas correspond to large d-values. The large values are due to the layered atomic arrangements in these mineral groups. The repeat distance between layers, called the basal spacing, is around 10 Å in most micas and repeat distance can be significantly greater in clays. The unit cells for most other kinds of minerals are too small to permit such large repeat distances and large d-values. So, if crystallographers see peaks at or below 10^o, they often know what general kind of mineral they have.