12.1.1: Intensity of Diffraction

Last updated
Save as PDF

Page ID: 18382

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

When discussing planes in unit cells, h, k, and l may have any integer values, which implies the possibility of an infinite number of d_hkl values that could satisfy Bragg’s Law. However, intense diffraction will only occur if many atoms occupy the (hkl) planes; without atoms no electrons are present to scatter X-rays. So, while Bragg’s Law tells us the angle at which diffraction could occur for any particular d_hkl value, it does not tell us anything about diffraction intensity.

Mineral unit cells contain a finite number of atoms, which restricts the number of d-values corresponding to planes of high atomic density. Therefore, the number of angles at which intense diffraction occurs is limited. An example in two dimensions will make this point.

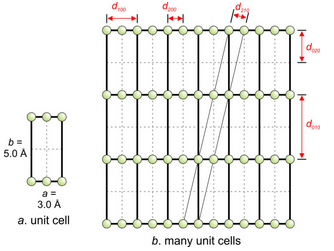
12.25.jpg — Figure 12.25: Hypothetical arrangement of atoms in a 2D crystal

Consider the hypothetical unit cell shown in Figure 12.25a. All atoms are on top and bottom edges. The unit cell has dimensions of a = 3.0Å and b = 5.0Å. Ignoring the third dimension (or assuming that all planes are perpendicular to the page), we can say that d₁₀₀ = 3.0Å and d₀₁₀ = 5.0Å.

If we imagine a structure made of many of these unit cells (Figure 12.25b), we see that many atoms are in rows 5.0Å apart, and diffraction corresponding to d₀₁₀ (5.0Å) should be quite intense. We can also expect apparent diffraction by the (020) planes (d = 2.5Å) to be intense, although no atoms occupy every other (020) plane. This is because we have no way of knowing diffraction order, and 2nd-order (n = 2) diffraction by (010) planes occurs at the same angle as 1st-order diffraction by (020) planes. So we will identify 2nd order (010) diffraction as (020).

Besides 010 and 020, 200 diffraction (d₂₀₀ = 1.5Å) will be quite intense because many atoms occupy the (200) planes. Note also that the (210) plains (diagonal in the figure) contain many atoms and should diffract almost as much as the (200) planes. Applying the equation in Box 12-1 above, we find that d₂₁₀ = 1.43Å, just about the same as d₂₀₀.

*(hkl)*	d	2θ
(210)	1.43	65.2^o
(200)	1.50	61.9^o
(020)	2.50	35.9^o
(100)	3.00	29.8^o

For our hypothetical crystal, (010) planes will cause very strong diffraction. (210), (200), and (020) planes will also cause significant diffraction. Applying Bragg’s Law to these d-values (see the table) tells us that the strongest diffraction will occur for a 2θ value of 29.8^o. Strong diffraction will occur for 2θ = 65.2^o, 61.9^o, and 35.9^o. But many other planes in this crystal will produce moderate or weak diffraction too.