11.12: Crystal Forms and the Miller Index

Last updated
Save as PDF

Page ID: 18460

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The replacement of unknown or variable numbers in a Miller index with h, k, or l allows us to make generalizations. The index (hk0) describes the family of faces with their third index equal to zero. A Miller index including a zero describes a face is parallel to one or more axes (Figure 11.66). The family of faces described by (hk0) is parallel to the c-axis (Figure 11.65); faces with the Miller index (00l) are parallel to both the a-axis and the b-axis (Figure 11.64c).

11.66.png — Figure 11.66: Forms and Miller indices

Figure 11.66a shows an orthorhombic prism with six faces. Some faces cannot be seen, but the Miller indices of all six are (100), (010), (001), (100), (010), and (001). Although this crystal contains three forms, indices for all faces contain the same numbers (two zeros and a one) but the order of numbers and the + or – sign changes.

Figure 11.66b shows an orthorhombic dipyramid. It contains only one form, and all the faces have the same numbers in their Miller index (332). This is always true for faces that belong to the same form; they always have similar Miller indices. This relationship is especially clear for crystals in the cubic system because high symmetry means that many forms may contain many identical faces.

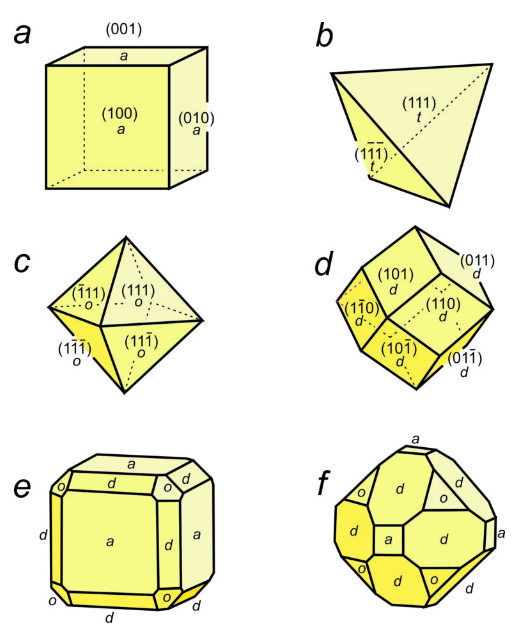
11.67.png — Figure 11.67: Some forms in the cubic system

The six identical faces on the cube in Figure 11.67a have indices (001), (010), (100), (001), (010), and (100). We symbolize the entire form {100}, and the { } braces indicate the form contains all faces with the numerals 1, 0, and 0 in their Miller index, no matter the order.

The four faces on the tetrahedron in Figure 11.67b, and the eight faces on the octahedron in Figure 11.67c are all equilateral triangles. For both, the form is {111}. As Figure 11.67b and c demonstrate, two crystals of different shapes can have the same form if they belong to different point groups. The tetrahedron in Figure 11.67b belongs to point group 43m; the octahedron in Figure 11.67c belongs to point group ⁴/_m3²/_m. If we know the point group and the form, we can calculate the orientation of faces. If a crystal contains only one form, we then know the shape of the crystal. Note that the cube, octahedron, and dodecahedron all belong to point group ⁴/_m3²/_m. The cubic form is {100}, the octahedral form is {111}, and the dodecahedral form in Figure 11.67d is {110}.

Figure 11.67e shows a crystal containing three forms: cube {100}, octahedron {111}, and dodecahedron {110}. Because they all belong to point group ⁴/_m3²/_m, we know the faces are oriented as shown. However, the crystal in Figure 11.67f belongs to the same point group and contains the same forms, but the size and shape of corresponding faces are different. We do not know the crystal shape if more than one form is present, unless we know some extra information.

Crystallographers sometimes label faces of the same form with the same letter as we have done in Figure 11.67. For some forms, the letter is just the first letter of the form name. For example, o indicates the octahedral form and d the dodecahedral form in the cubic system. Usually, however, the symbols are less obvious (we normally designate cube faces, for example, by the letter a); labels also vary from one crystal system to another.