11.10: The Miller Indices of Planes within a Crystal Structure

We use Miller indices to describe the orientation of crystal faces, but we also use them to describe planes within a crystal structure. For example, we may be interested in knowing which planes in a unit cell contain the most atoms. For planes within a cell, we calculate Miller indices as we do for crystal faces, except that we do not clear common denominators after inversion of axial intercepts.

For example, if we calculate an index of (633) for a set of planes, we do not divide by 3 to give (211), as we do when calculating a Miller index for a crystal face. We do not do this because, besides orientation, the spacing and location of planes are important when we are talking about atomic arrangements and other aspects of crystal structures, and not talking about crystal faces.

Figure 11.65: Planes in unit cells

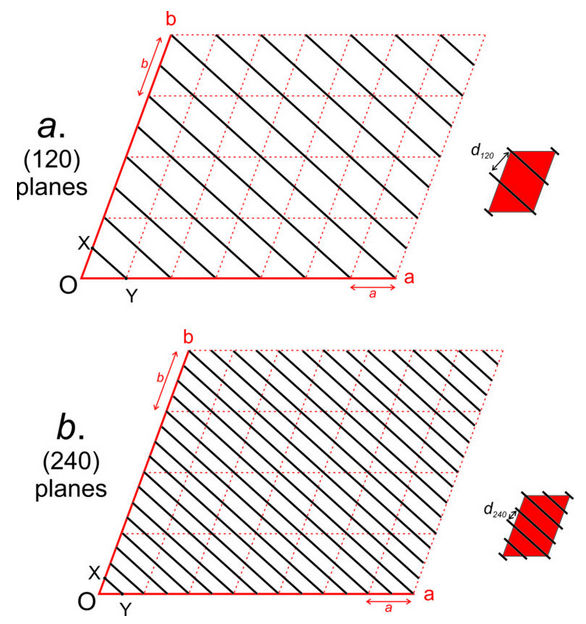
Figure 11.65a shows some two-dimensional unit cells cut perpendicular to the c-axis. The plane passing through points X and Y (and perpendicular to the page) has axial intercepts 1, ¹/₂, ∞, so its Miller index is (120). Because all unit cells are equivalent, we know identical (120) planes exist in all the unit cells.

Drawing a shows all equivalent (120) planes; when we discuss (120) planes within a crystal, we refer to this entire family, not just to one plane. As shown in the red inset drawing, four (120) planes intersect each unit cell. Two pass through the inside of the cell, and two through corners. Note that the axial intercepts of the (120) plane closest to the origin (O) are 1, ¹/₂, ∞, equivalent to ¹/_h, ¹/_k, ¹/_l for the entire family of planes. This relationship holds true for any family of (hkl) planes.

Different families of planes, with the same orientation but different spacings, have different indices. The drawings in Figure 11.65b show planes spaced half as far apart as the (120) planes; d₂₄₀ = ¹/₂ d₁₂₀. The plane closest to the origin has intercepts ¹/₂, ¹/₄, ∞. Inversion gives the Miller index (240). We do not clear the common denominator (divide by 2) because the families of (240) and (120) planes, although parallel, are not identical. There are twice as many (240) planes. The red inset drawing shows that seven (240) planes intersect each unit cell – two at opposite corners; the rest pass through the cell interior.

Because the Miller indices (120) and (240) are proportional, the two families of planes are parallel but the (240) planes are spaced apart half as much as the (120) planes. This is always the case – proportional indices mean planes are parallel and larger indices mean planes are closer together. If we are considering a set of planes that cause X-ray diffraction (discussed in detail in the next chapter), we describe them with Laue indices. These indices are the same as Miller indices, but we omit the parentheses. Thus we can have 120 or 240 diffraction, and the angle of diffraction is different because the two families of planes have different spacings.