11.8.4: Planes in Crystals

While crystals and crystal faces vary in size and shape, Steno’s law tells us that angles between faces are characteristic for a given mineral. The absolute location and size of the faces are rarely of significance to crystallographers, while the relative orientations of faces are of fundamental importance. We can use face orientations to determine crystal systems and point groups, so having a simple method to describe the orientation of crystal faces is useful.

Figure 11.64a shows three axes with different unit cell lengths; small red dots show unit increments along the axes. The axes are orthogonal, so this arrangement corresponds to the orthorhombic system. Consider a plane parallel to a crystal face. Such a plane may be parallel to one axis (Figure 11.64b), parallel to two axes (Figure 11.64c) or it may intersect all three axes (Figure 11.64d).

Figure 11.64: Axial intercepts and Miller indices

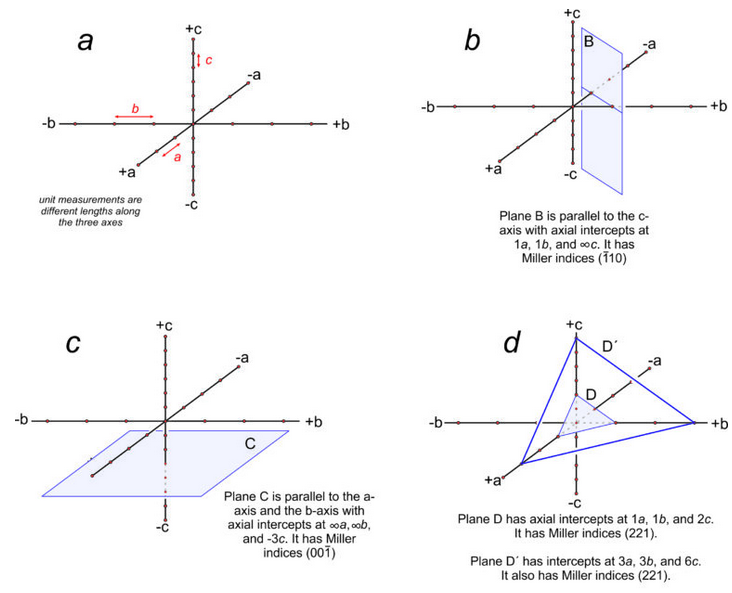
We can describe the orientation of a plane by listing its intercepts with the axes. For a face running parallel to an axis, the intercept is at ∞ (because the face never intersects the axis). In Figure 11.64b, the plane is parallel to the c-axis but intersects the a-axis and b-axis one unit from the origin. So, it has axial intercepts 1a, 1b, and ∞c, which we shorten to 1, 1, ∞. In Figure 11.64c, the plane is parallel to two axes and has axial intercepts ∞a, ∞b, 3c, or simply ∞, ∞, 3.

Crystal faces are commonly parallel to axes, but the use of ∞ to describe their orientations can be confusing and awkward. A second problem with using intercepts to describe face orientation is that parallel planes, such as plane D and plane D´ Figure 11.10d, have different intercepts. Crystallographers find this inconvenient because crystals may be large or small, but face orientation, not size, is generally the feature of greatest significance. To avoid these and other problems, crystallographers do not report axial intercepts. They use Miller indices instead.