11.5.1: Space Group Operators
- Page ID
- 18449
In 3D, we assign atomic arrangements to different space groups that have different space symmetries. Each space group is characterized by a combination of one of the 14 Bravais lattices with a unit cell that has a particular symmetry. We call the different kinds of possible symmetry operators, collectively, space group operators. Space symmetry includes the point group symmetries that we discussed previously. And it also includes glide planes and screw axes. We briefly introduce these above in Box 11-1. These two are special kinds of space group operators that involve combinations of point symmetry and translational symmetry, in much the same way that rotoinversion axes involve rotation and inversion applied simultaneously.
11.5.1.1 Glide Planes
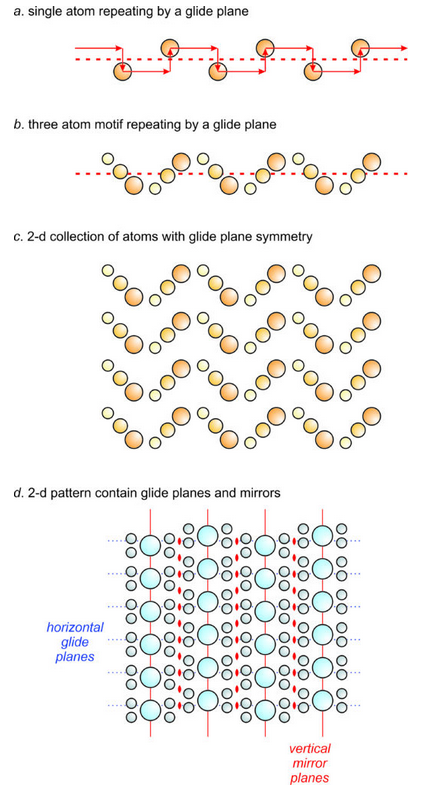
Glide planes differ from normal mirror planes because they involve translation before reflection. Figure 11.44 shows some examples. In drawing a, a single atom is repeated by a horizontal glide plane (dashed red line). The red arrows show how the atom repeats by translation followed by reflection. In drawing b, a three-atom motif repeats according to a horizontal glide plane. And in drawing c, we see a 2D pattern with glide plane symmetry. The pattern contains no mirrors, rotation axes, and no inversion center. Yet, it contains significant symmetry.
Space group operators and other symmetry elements combine in many ways. For example, Figure 11.44d shows a pattern that contains horizontal glide planes (blue dotted lines) and vertical mirror planes (solid red lines). As we have seen previously, combination of symmetry elements often requires other symmetry to be present. The combination of a glide plane with a mirror means that this pattern contains 2-fold rotation axes (red lens shapes). This pattern has symmetry equivalent to plane group 2mg depicted in Figure 11.31 (in Box 11-1).
Figure 11.45 shows a glide plane in three dimensions; a motif of 8 atoms repeats by vertical translation and reflection. This figure involves a simple motif with lots of space around it. The arrangements of atoms in most minerals are generally more complicated and difficult to draw in 3D in a way that shows their symmetries clearly. In part, this is because a glide plane affects all atoms in a structure, not just the ones adjacent to the plane as seen in Figure 11.45.
Atomic arrangements may contain any of six symmetry elements involving reflection, singly or in combination. These include proper mirror planes and 5 different kinds of glide planes. Glide planes may have any of the orientations that mirror planes can have. So, they may be parallel to the a-, b-, or c-axis, parallel to a face diagonal, or parallel to a main (body) diagonal. For most glide planes, the magnitude of the translation (t) is half the unit cell dimension in the direction of translation. The direction of gliding distinguishes different glides and allows us to classify them. The table below summarizes the possibilities.
| Space Symmetry Operators Involving Reflection | |||
| operator | type of operation | orientation of translation | translation* |
| m a b c n d |
proper mirror axial glide axial glide axial glide diagonal glide diamond glide |
none parallel to a parallel to b parallel to c par. to a face diagonal par. to main diagonal |
none 1/2 a 1/2 b 1/2 c 1/2 t 1/4 t |
| *t = the unit cell dimension in the direction of translation | |||
For further discussion of glide planes, check out the video that is linked here:
11.5.5.2 Screw Axes
Screw axes result from the simultaneous application of translation and rotation. We combine 2-, 3-, 4-, or 6-fold rotation operators with translation to produce these symmetry elements. Many combinations are possible. Figure 11.46 shows a few examples.
A screw axis has the appearance of a spiral staircase. We rotate a motif, translate it, and get an additional motif. As with proper rotation axes (rotation axes not involving translation), each n-fold screw operation involves rotation of 360o/n. After n repeats, the screw has come full circle. The translation associated with a screw axis must be a rational fraction of the unit cell dimension or the result will be an infinite number of atoms, all in different places in different unit cells.
We label screw axes using conventional symbols. In Figure 11.46, they are 61, 41, 31, and 21. In the labels, the large 6, 4, 3, or 2 signifies 6-fold, 4-fold, 3-fold, or 2-fold rotation. The subscript tells the translation distance. A 61 screw axis, for example, involves translation that is 1/6 of the unit cell dimension in the direction of the screw axis. 41, 31, and 21 axes involve translations that are 1/4, 1/3, and 1/2 the unit cell dimension. Similarly, 62, 63, 64, and 65 screw axes (not shown) would involve translations of 2/6, 3/6, 4/6, and 5/6 of the cell dimension.
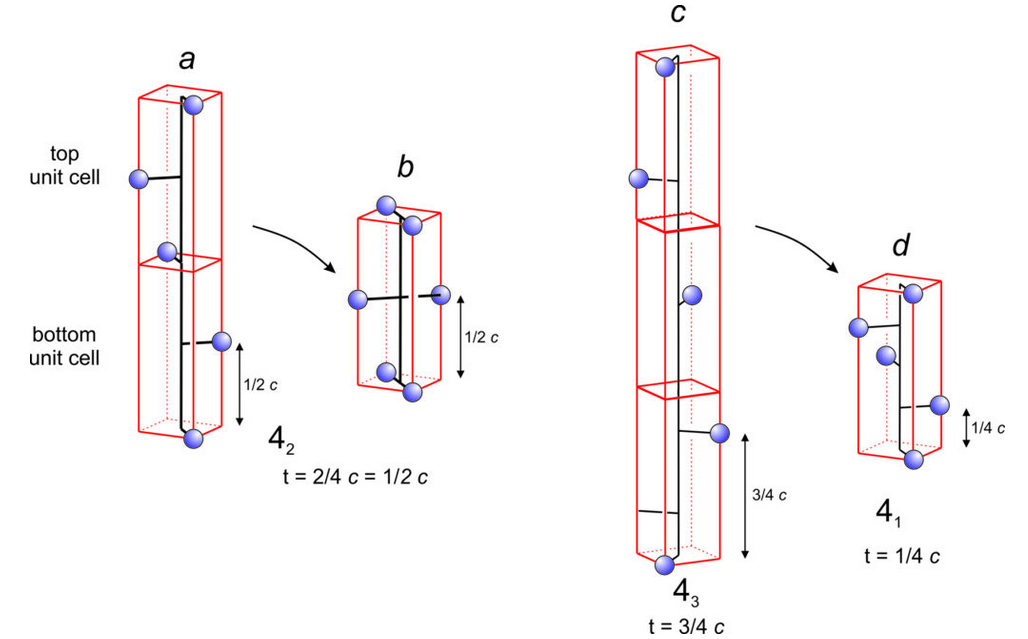
Figure 11.47a shows application of a 42 operator to a single atom. The translation distance is 1/2 the unit cell height, and we must go through four 90o rotations and two unit cells to get another atom that is directly above the starting atom. All unit cells must be identical, but the 42 operation gives a bottom and top unit cell with atoms in different places. The only way this operator can be made consistent is to add the extra atoms shown in Figure 11.47b. In other words, the presence of a 42 axis requires the presence of a 2-fold axis of symmetry.
Figure 11.47c shows a 43 axis and 11.44d shows a 41 axis. After four applications of either operator the total rotation is 360°, bringing the fourth point directly above the first. For the 41 axis, after four applications the total translation is equivalent to one unit cell length. But for the 43 axis it is three unit cell lengths because the translation is 3/4 of the unit cell. The only way the 43 operator can be made consistent is to add the extra atoms shown in Figure 11.47d. Note that the 43 and 41 axes produce patterns that are mirror images of each other. The two axes are an enantiomorphic pair, sometimes called right-handed and left-handed screw axes.
When all combinations are considered, we get the 21 possible rotation axes (either proper rotation axes or screw axes) listed in the table below. As with proper rotational axes, some screw axes are restricted to one or a few crystal systems. For example, 31 and 32, which are an enantiomorphic pair, only exist in the rhombohedral system. Similarly, the 6n axes only exist in the hexagonal system.
| Space Symmetry Operators Involving Rotation | |||
| operator | type of operation | rotation angle | translation* |
| 1 1 2 21 2 3 31 32 3 4 41 42 43 4 6 61 62 63 64 65 6 |
identity inversion center proper 2-fold 2-fold screw mirror proper 3-fold 3-fold screw 3-fold screw 3-fold rotoinversion proper 4-fold 4-fold screw 4-fold screw 4-fold screw 4-fold rotoinversion proper 6-fold 6-fold screw 6-fold screw 6-fold screw 6-fold screw 6-fold screw 6-fold rotoinversion |
360o 360o 180o 180o 180o 120o 120o 120o 120o 90o 90o 90o 90o 90o 60o 60o 60o 60o 60o 60o 60o |
none none none 1/2 t none none 1/3 t 1/3 t none none 1/4 t 2/4 = 1/2 t 3/4 t none none 1/6 t 2/6 = 1/3 t 3/6 = 1/2 t 4/6 = 2/3 t 5/6 t none |
| *t = the unit cell dimension in the direction of translation | |||
For a further discussion of screw axes, check out the video that is linked here: