10.1.1: Introduction
- Page ID
- 18464
The shape of a crystal reflects its internal atomic arrangement, and the most important aspect of a crystal’s shape is its symmetry. As defined by the ancient Greek philosopher Aristotle, symmetry refers to the relationship between parts of an entity. Symmetry may be of many sorts. For example, a hexagon has 6-fold symmetry; we can rotate it 60o six times and get back to where we started. And wallpaper that contains a repeating pattern of some sort has symmetry; the pattern repeats with even spacing vertically and horizontally. Zoltai and Stout (1984) give an excellent practical definition of symmetry as it applies to crystals: “Symmetry is the order in arrangement and orientation of atoms in minerals, and the order in the consequent distribution of mineral properties.”
Figure 7.54 (Chapter 7) showed the atomic arrangement in halite. Halite, like all minerals, is built of fundamental building blocks called unit cells. In halite crystals, the unit cells have a cubic shape. Fluorite, too (Figure 7.55, Chapter 7) has a cubic unit cell. Figures 10.2, 10.3, 10.4, and 10.5, below, show other minerals with an overall cubic arrangement of their atoms. Diamond’s atomic arrangement is quite simple because it only contains carbon. Cuprite is a bit more complicated because copper and oxygen atoms alternate. Sodalite and garnet are even more complicated. But, all these minerals have cubic unit cells. The unit cells have what is called cubic symmetry.
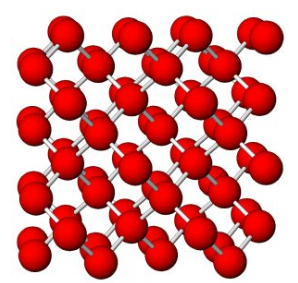


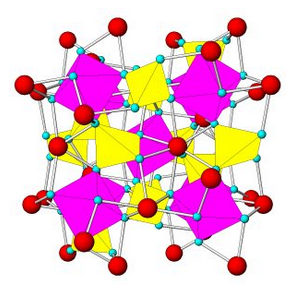
Unit cells may have any of six fundamental shapes with different symmetries. Cubic unit cells, which have the most symmetry possible, may stack together to produce an irregularly shaped crystal that displays no symmetry. But, they may also stack together to create crystals with six identical faces at 90o to each other (a cube). Minerals with shoe-box shaped unit cells, in contrast, cannot form cubic crystals. And, as we will see, unit cells with less symmetry (that are neither cubic nor shoe-box shaped) cannot combine to form crystals that are cubic or crystals that are shoe-box shaped. So, the symmetry of the unit cell limits possible crystal symmetry.
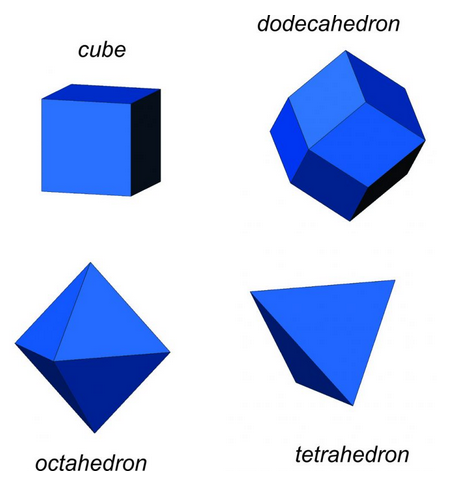
Although the relationship between a cubic arrangement of atoms and a cube-shaped crystal may seem clear, things are not always so simple. Halite has a cubic unit cell, and euhedral halite crystals are generally cubes like the one shown in Figure 10.6. And, cuprite crystals (Figure 10.3) may be cubes, too, but they are also sometimes octahedra (Figure 10.6). Notice that octahedra are equivalent to cubes with their corners removed and replaced with crystal faces. Cubes and octahedra, and also dodecahedra and tetrahedra (Figure 10.6) are all closely related because they are made of cubic unit cells, and the atomic arrangement in each is the same in three perpendicular directions.
Sodalite (Figure 10.4) and garnet (Figure 10.5) both have cubic unit cells but typically form rhombic dodecahedral crystals. (There are different kinds of dodecahedra but for brevity, when we refer to a dodecahedron in the rest of this chapter we are talking about a rhombic dodecahedron, such as the one seen in Figure 10.6.) And, diamond (Figure 10.2) crystals may be octahedra, dodecahedra, cubes, and tetrahedra. Figure 10.6 shows those possible crystal shapes. These crystals all look different, and have different numbers of faces, yet all of these have the same shaped (cubic) unit cells.
So, we see that if the atomic arrangement has cubic symmetry, a crystal may or may not be cubic. And, it may or may not have the same symmetry as a cube. But, we can turn this around. If a crystal shows some kind of symmetry, the atoms within it must be arranged with at least that much symmetry. They may have more. For example, as we will see later in this chapter, crystals of many different shapes must have cubic atomic arrangements, even though the crystals are not cubes. Thus, the external symmetry of a crystal tells us about the atomic arrangement within. In this chapter, the focus is on crystal symmetry. In the following chapter we will look more closely at the atomic arrangements implied by that symmetry.
For an introduction to the different types of symmetry that crystals may have, watch the video linked below:


