4.1: Crystalline and Noncrystalline Solids
- Page ID
- 17533
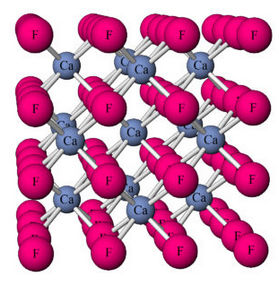
By definition (with just a few special exceptions) minerals must be crystalline. This means that they are solids with an orderly repetitive atomic arrangement. For example, this ball and stick model (Figure 4.2) shows the atomic arrangement in fluorite (CaF2).
Fluorite is one of a small number of common minerals that are isotropic. Isotropic minerals have very symmetrical atomic arrangements and atoms are arranged in an overall cubic pattern. The same atoms are encountered in any direction through the mineral and, consequently, mineral properties are the same all directions. The photo in Figure 4.3 shows light purple cubic fluorite crystals. They are interpenetrating deformed cubes. Many spectacular specimens of cubic fluorite crystals like this one are found in museums.

Other isotropic minerals, besides fluorite, include diamond (C), almandine (Fe3Al2Si3O12), gold (Au), pyrite (FeS), silver (Ag), spinel (MgAl2O4), and sodalite (Na3Al3Si3O12•NaCl). All these minerals, have a cubic arrangement of atoms, although their crystals may not be cubes. Still, their crystals, when euhedral, are equant and generally have many identical faces.
Most minerals, however, are anisotropic. This means that they have different properties in different directions. Consequently, their crystals are not as symmetrical as fluorite’s. Yet, crystals may possess other symmetry, even if they do not resemble a cube.

So, well-formed mineral crystals often exhibit symmetry. But, it may not be cubic symmetry like fluorite – other shapes are possible. For example, the blue-gray barite (BaSO4) crystals seen in this photo are tabular and have a long, an intermediate, and a short dimension. The shape, termed orthorhombic, is similar to the shape of a shoebox.
Barite is an anisotropic mineral. The crystals have lots of symmetry, but it is different from the symmetry of fluorite. Still, when compared with many minerals, barite crystals are quite symmetrical. Olivine, topaz, some pyroxenes, and topaz all sometimes have crystal shapes similar to barite’s.

Some mineral-like substances are noncrystalline, also described as amorphous, which means they have a random atomic structure. Natural volcanic glass, obsidian, is an example. This photo (Figure 4.5) shows a specimen of snowflake obsidian. It contains black volcanic glass (obsidian) with white patches. Obsidian is noncrystalline, but over time it will sometimes begin to crystallize, creating the white patches seen here. The patches consist of cristobalite, a variety of SiO2 that is a polymorph of quartz.
Amorphous solids are generally isotropic, so they have the same properties in all directions. This gives the materials properties that are sometimes very useful. For example, window glass is made by melting mixtures containing mostly quartz sand, and allowing the melt to solidify quickly so atoms cannot arrange themselves in a crystalline structure. The process produces a noncrystalline isotropic glass, so light can pass through it equally well in all directions. This is one reason why manufactured glass makes a better window than transparent minerals.
Making Glass from Minerals

Glass manufacturers make glass by melting ingredients and cooling the melt so quickly that crystals cannot form. The most common kind of glass, which is used to make bottles or window panes, is soda-lime-silica glass. People have manufactured similar glasses since Roman times.
Soda-lime-silica glasses typically contain about 75 wt% SiO2, 15 wt% Na2O, and 10 wt% CaO. Raw ingredients are usually the minerals quartz (SiO2), trona [Na3H(CO3)2•2H2O], and calcite (CaCO3). In the United States, we obtain high-quality quartz and calcite from many places. Most of the trona comes from the Green River Formation in Wyoming, where trona beds are up to 9 m (30 ft) thick.
Glass manufacturers heat the mineral ingredients to between 1,550 and 1,600 °C (2,820 and 2,910 °F), producing a homogeneous melt as CO2 and H2O escape into the atmosphere. Quenching, to produce a final glass, is done in various ways depending on the product wanted.
Manufacturers change glass properties by adding small amounts of other ingredients. The addition of boron produces heat-resistant glass such as Pyrex® or Vycor®. Lead gives glass the optical properties needed for making imitation crystals. Aluminum can make glass resistant to weathering. Fluorine makes glass opaque. Lithium reduces the melting point of glass. Trace amounts of metals change glass color: iron makes glass green, nickel makes it brown or orange, and cobalt makes it blue.


