2.6: Problem Set Part 1- Analyzing Tide Gauge Records and DART Data
- Page ID
- 6995
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tide gauge records from 2004 and DART data from 2011

In the following analysis, you'll work with tide gauge records from stations around the world that recorded the tsunami generated by the 26 December 2004 Sumatra-Andaman earthquake. Then you will work with data recorded by Pacific Ocean DART stations from the 2011 Tohoku-Oki earthquake. It is fine with me to complete this analysis in whatever way works best for you. You may all work together to do this activity or you may want to work in groups or by yourselves. No matter how you choose to go about it, please write up and submit your analyses individually and in your own words. This activity is due at the end of the first week of this lesson.
Tsunami Data Problem Set
Part 1: Checking out four tide gauges from 2004
Save the Tide Gauges Problem Set Worksheet to your computer by right-clicking (control-click on a Mac) on the link above and selecting "Save link as..."

TIP!!
You should use the worksheet for writing down your answers but you should leave this web page open while you work on the problem set. WHY? Because I explain how to do most of the analysis right here. The worksheet is just so you don't have to retype the questions yourself.
Below are four record sections. These data come from tide gauges maintained by the University of Hawaii with support from NOAA. Review each record section, then answer the associated questions on your worksheet.
Record 1: Salalah, Oman
Before you begin, let's look at Salalah's record together:
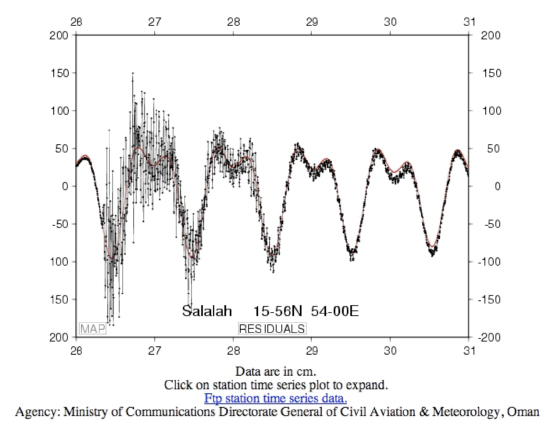
- Click for a text description of Figure 2.6.
- I want to show you this tide gauge record and walk you through a bit of how to look at it because I think many of you are not familiar with looking at this kind of data. The first thing to see is that right here on the record it is telling you where it is from. This data is from Salalah, Oman. The coordinates of the station are given. It is at 15 degrees and 54 minutes north latitude and it is at exactly 54 degrees east longitude. There are 60 minutes in a degree and there are 60 seconds in a minute. For later calculations, we are going to want to change this to decimals and I will show you how to do that later on. Now let us look at the x-axis and the y-axis. That is the first thing to do if you are looking at unfamiliar data. So here is the y-axis. It goes from -200 to 200. That is in centimeters and it is referenced to some kind of arbitrary mean which is zero. The important thing here is to get the scale right, not necessarily the absolute values. The x-axis is in days. This is December 26, 2004, and here is December 31, 2004. There are 5 days of data shown here. Inside the plot, you can see there are two things. There is a red line. And there is a bunch of black points connected by a line. Let us look at the red line first. The red line is actually not data. It is a model prediction of what the tides should be. You can calculate this, so people routinely do this and it can help you figure out if your tide gauge is working very well or not. This place has kind of an interesting tidal signature, which is a little bit beyond the scope of this course but it is cool to look at anyway. Here is a high tide and a low tide and another high tide. Out here, the black lines, which are the data actually matching the model pretty well, which is good. At the beginning of this record, you can see that it is matching pretty well. In this area from about here to about here, the data does not match the model very well at all. You can see the red line back in the back here. and the data are all these little black points connected up by a line. The reason the data does not match the model in this interval is that the tsunami arrives at this station right about here. This earthquake happened at about 1 am UTC time on the 26th and it takes a little while to get to this station. You can see these huge amplitude excursions from what the regular tide should be. The difference between where the sea level should be and where it actually is is why the tsunami is so dangerous.
1.1 The latitude and longitude of this station are given in degrees and minutes. (i.e. 15-56 N means 15° 56' North latitude and 54-00 E means 54° 00' East longitude). Each degree contains 60 minutes. For later calculations, we will want to use decimal degrees instead of minutes. Convert the latitude and longitude of this station to decimal degrees. HINT for getting started: If the latitude were 12-13 N, meaning 12° 13' N, this would equal 12.22° because 13/60 = 0.22.
1.2 Let’s look at the axes and data now. The X-axis is showing time and the Y-axis is showing water height. The X-axis ranges from 26 to 31. These are days of December 2004. The Y-axis ranges from -200 to +200 cm. Now let's look at what is being plotted here. The black line connects data measurements shown by small black dots. The red line is a prediction of the tidal signature at this station. Okay, what are the obvious things to see here? You should be able to discern the approximate arrival time of the tsunami. When is it? Where on this record is the prediction of wave height doing a good job and where is it failing? Why does the prediction fail where it does? For about how long does the tsunami have a significant impact on the wave height at this station?
1.3 Look at the background tidal signature. Describe the tidal cycle for one 24-hour period.
1.4 What is the normal tidal amplitude? Compare this with the amplitude of the tsunami. Keep in mind that the tsunami amplitude is superimposed on top of the tidal signature.
Record 2: Ranong, Thailand
This record looks a lot different from the record at the Salalah station. This is an analog recording made with a pen connected to a cylindrical paper drum that turns continuously at a set pace. It doesn't take much perusing to see why digital data is preferred for most scientific measurements. For one thing, if somebody doesn't come along and change the paper every 24 hours, the record of each successive day prints over the record of the previous day as the tidal cycles repeat. On the other hand, I think this record looks really cool. There's something about analog records that just seem more lifelike. They aren't totally useless, either. What can we find out from inspecting this record? First, let's look at it together, then you can answer the questions.
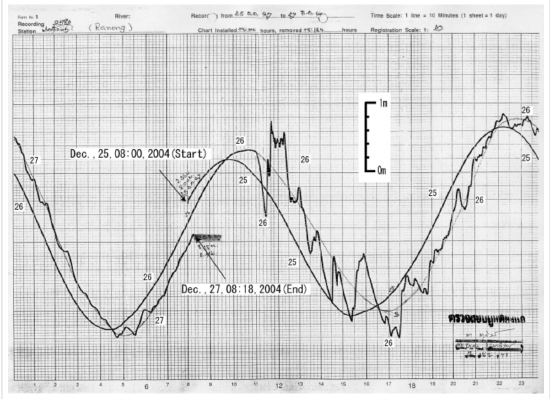
- Click for a text description of Figure 2.7.
- Now let us look at this record from Ranong, Thailand. I hope you can see right away that this one looks a whole lot different from the last one we just looked at. The reason why is that this is analog data. The way this works is that you have got this gridded piece of paper. It is attached to a cylindrical drum that continuously rotates. There is a pen attached to a spring that writes on the paper. When the spring receives an electrical impulse from the height of the water changing the pen follows along and you can see the tides that way. Let us do what I like to do when I am encountering new data that I have never seen before which is to first check out the axes and see what they say and then look at what is plotted after that. Let us look at the x-axis first. Up here it says time scale: 1 line equals 10 minutes and one sheet equals one day. Okay, so this is a sheet. This whole thing is one day. If we look down here we see the numbers 1, 2, 3, 4 up to 23. Each of these heavier lines is an hour, and these little thinner vertical lines are 10 minutes. The y-axis is a little harder to read because it is not printed anywhere along the side. But they have got this little floating scale here that tells you what a meter is. In between these heavy lines is a meter. Now let us look at what is plotted. This data record starts right here on December 25, 2004, at 8 o'clock in the morning. We can confirm that by seeing where the pen mark starts and going down here and seeing that there is the 8. We can see a high tide here and a low tide here. Here is another high tide and now we get to midnight. And my guess is that all the operators were on holiday because nobody came along and changed the paper. The drum keeps turning around and so when it got to be the 26th it just overprinted what the previous record was. So we go over here to the left and here is December 26 and the line is being drawn along and right here is where the tsunami arrives. You can see a big excursion from this little skinny line back here which is the model prediction of what the tides should be. You couldn’t even see it before because the model and the data matched so well. Now that we have the tsunami you can see the model prediction. The tsunami affects height at this station well into the next day. Here is midnight on the 26th, still nobody came and changed the paper. Now here comes the 27th, and this record ends on December 27 at 8:18 in the morning.
1.5 The time scale on the X-axis is given up in the right-hand corner of the record. It says "Time scale: 1 line = 10 minutes (1 sheet = 1 day)". Okay, so take a look at the grid. What do the numbers on the X-axis refer to? How many days are shown in this record?
1.6 The vertical scale is given. (It's floating in the middle of the record.) What is the normal tidal amplitude at this station?
1.7 Comment on the differences you note between the tidal cycle at this station and at the Salalah station. Comment on the differences you note between the normal tidal amplitude here and at Salalah and the differences between the tsunami amplitude at this station compared to the Salalah station. Why are there differences?
1.8 Notice that because of the fact that more than one day is shown on this record, you can see that the tidal peaks and troughs are offset slightly as the days go by. Tides do not have a period that fits exactly into one day. That is, the peak-to-peak time is not exactly 12 hours. Approximately what is the period? (If you live near the coast, or have spent any time near the ocean, you already knew that the time of the high and low tides change predictably as the days go by. Isn't it reassuring when recorded data confirms what an observant person already knows! Science works!)
1.9 When does the tsunami arrive at Ranong? What is the amplitude of the tsunami compared to the background tidal amplitude? For about how long does the tsunami affect sea level height at Ranong? Compare these answers with your observations of the records from Salalah station.
Record 3: Syowa, Antarctica
I think you should now be able to interpret this plot on your own. Try it!
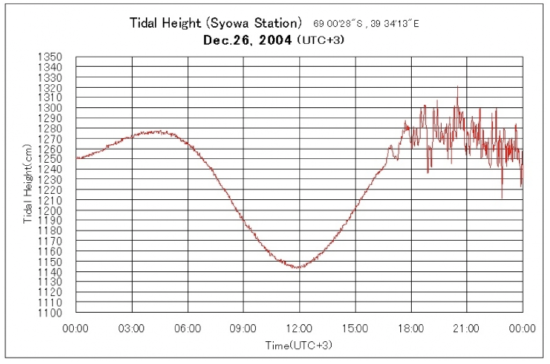
1.10 The coordinates of this station are given in degrees, minutes, and seconds. There are 60 minutes in each degree and 60 seconds in each minute. Convert the station coordinates to decimal degrees.
1.11 The local time at this station is "UTC +3". This means that this station is three hours ahead of "Universal time", which is set for historical reasons at Greenwich, England, where the longitude is zero. Find out the difference between UTC and the time in your hometown. (Your computer probably knows. Otherwise, a quick web search should accomplish this task.) Remember to cite the place where you found the answer.
1.12 What are the units of the X and Y axis on this record?
1.13 When does the tsunami arrive?
1.14 What is the tsunami amplitude compared to the normal tidal amplitude? Compare this to your observations at the previous stations.
Record 4: Rodrigues Island
HMM! What is going on at this station? The red line shows the tidal prediction and the black and blue lines show data.
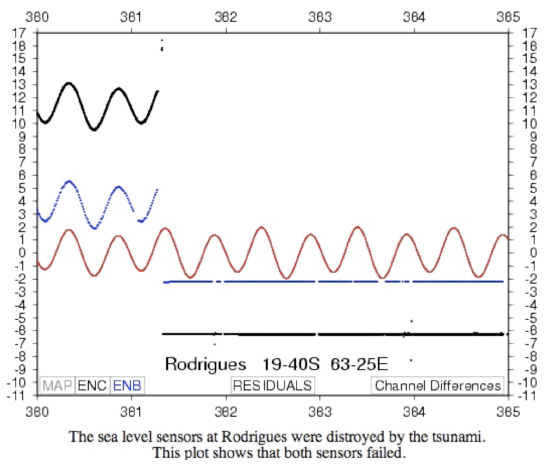
1.15 The latitude and longitude are given for this station in degrees and minutes. Convert to decimal degrees.
1.16 The X-axis is given in "Julian days" of 2004. Julian days are numbered consecutively from 1 to 365 (or 366 in leap years). So January 1 is Julian day 001, February 1 is Julian day 032. What is the Julian day of your birthday? Convert the values of the X-axis from Julian days to normal dates. (To get this answer, you have to recall whether 2004 was a leap year or not.)
1.17 Read the text given by the spelling-challenged station operator as part of this record section. Now, look at the data records. When does the tsunami arrive? What happens to the data at this point? Why does the red line continue uninterrupted?
Part 1 Summary
This is probably a good time to point out that data isn't always perfect. Sometimes hardware fails, as in this case. Sometimes errors and uncertainties are introduced in other ways. We will discuss measurement error and uncertainty more fully in the next part of the problem set.
You have finished Part 1 of this problem set! Proceed to Part 2 on the next page.


