12.1: Waves and Wave Processes
- Page ID
- 6916
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Waves are created when wind blows over the surface of the water. Energy is transferred from wind to the water by friction and carried in the upper part of the water by waves. Waves move across the water surface with individual particles of water moving in circles, the water moving forward with the crest and moving backward in the trough. This can be demonstrated by watching the movement of a cork or some floating object as a wave passes.
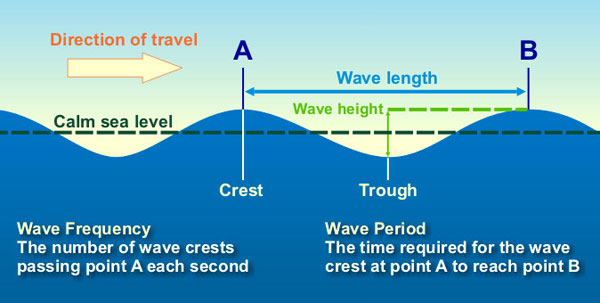
Important terms to understand in the operation of waves include: Wave crest is the highest point of the wave; the trough is the lowest point of the wave. Wave height (equal to twice wave amplitude) is the vertical distance from the trough to the crest and depends on the amount of energy carried in the wave. Even before reaching shore, wave height increases with increasing wave energy. Wavelength is the horizontal distance between adjacent wave crests or corresponding features of the wave. Wave velocity is the speed by which a wave crest moves forward, which is also related to the energy carried by the wave. Wave period is the time interval it takes for adjacent wave crests to pass a given point.
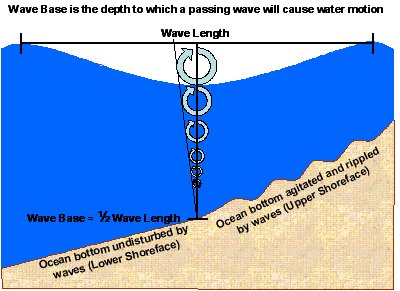
The circular motion of water particles diminishes with depth and is negligible at about one-half wavelength, an important dimension to remember in connection with waves. The vertical reach of waves in the water is called the wave base. Looking at incoming waves at a beach, one will appreciate that most ocean waves have a wavelength on the order of a few tens of feet. Thus, seawater is typically disturbed by a wave motion to a depth of a few tens of feet. This is known as a fair-weather wave base. In strong storms such as hurricanes, both wave length and the maximum depth of water disturbance increase dramatically. The effective depth to which waves can erode sediment is thus called a storm wave base, which is approximately 300 feet [1].
Waves are generated by wind blowing across the ocean surface. The amount of energy imparted to the water depends on the wind velocity and the distance across which the wind is blowing. This distance is called fetch. Waves striking a shore were typically generated hundreds of miles from the coast by storms and may have been traveling across the ocean for days.
Winds blowing in a relatively constant direction generate waves moving in that direction. Such a group of approximately parallel waves traveling together is called a wave train. As wave trains spread from different areas of generation, they may move in different directions and carry different amounts of energy. Interaction of these different wave trains produces the choppy sea surface seen in the open ocean. Also of interest is that many wave lengths are produced in a given wave train from a fetch region. Longer waves travel at a faster velocity than shorter wavelengths thus there is a sorting of wavelengths that takes place during travel of the wave train with the longer waves arriving first at a distant shore. This is a process called wave dispersion.
Behavior of Waves Approaching Shore
 CC BY-SA 3.0 or GFDL], via Wikimedia Commons: This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license." width="238" src="/@api/deki/files/7980/Breaking_wave_types.svg_-238x300.png">
CC BY-SA 3.0 or GFDL], via Wikimedia Commons: This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license." width="238" src="/@api/deki/files/7980/Breaking_wave_types.svg_-238x300.png">On the open sea, waves generally appear choppy because wave trains from many directions are interacting with each other. Where crests converge with other crests (called constructive interference) they add together producing peaks, a process referred to as wave amplification. Constructive interference of troughs produces hollows. Where crests converge with troughs, they cancel each other out (called destructive interference). As waves approach the shore and begin to make frictional contact with the seafloor (i.e., water depth is a half wavelength or less) they begin to slow down, but the energy carried by the wave remains the same so they build up higher. Remember that the water moves in a circular motion as the wave passes, with the water that feeds each circle being drawn from the trough in front of the advancing wave. As the wave encounters shallower water at the shore, there is eventually insufficient water in front of the wave to supply a complete circle, and the crest pours over creating a breaker.
A special type of wave is generated by any energetic event affecting the seafloor, such as earthquakes, submarine landslides, and volcanic eruptions. Such waves are called tsunamis and, in the case of earthquakes, are created when a portion of the seafloor is suddenly elevated by movement in the crustal rocks below that are involved in the earthquake. The water is suddenly lifted and a wave train spreads out in all directions from the mound carrying enormous energy and traveling very fast (hundreds of miles per hour). Tsunamis may pass unnoticed in the open ocean because the wavelength is very long and the wave height is very low. But as the wave train approaches the shore, each wave makes contact with the shallow seafloor, friction increases, and the wave slows down. Wave height builds up and the wave strikes the shore as a wall of water a hundred or more feet high. The massive wave may sweep inland well beyond the beach. This is called the tsunami runup, which destroys structures far inland. Tsunamis deliver a catastrophic blow to observers at the beach as the water in the trough in front of it is drawn back toward the tsunami wave, exposing the seafloor. Curious and unsuspecting people on the beach may run out to see exposed offshore sea life only to be overwhelmed when the breaking crest hits.


