4.3.2: The Energy Balance
- Page ID
- 15862
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Available net radiation is used to do work in the Earth system. The principal use of this energy is in the phase change of water (latent heat, LE), changing the temperature of the air (sensible heat, H), and subsurface (ground heat, G) or,
Q* = H + LE + G
Though there are other uses for net radiation like photosynthesis and the weathering of rocks, it is the three previously stated uses that are most important. LE, H, and G involve non-radiative transfers of heat. That is, conduction or convection/advection are responsible for the transfer of heat, not electromagnetic radiation.
When work is done, like heating the air above the surface, there is a transfer of energy (heat) from one place to the next. To illustrate the transfer of energy we'll use arrows either pointing away from or toward the surface of the Earth to indicate the direction of heat transfer. We will also use positive and negative signs to indicate that heat is being added to, or taken away from a body. Following the conventions of Sellers (1965) and Oke (1987), non-radiative fluxes directed away from a surface are positive. Thus positive values indicates a loss of heat from the surface while negative values indicate a gain.
Sensible Heat Transfer (H)

Sensible heat is heat energy transferred between the surface and air when there is a difference in temperature between them. A change in temperature over distance is called a "temperature gradient". In this case, it is a vertical temperature gradient, i.e., between the surface and the air above. We feel the transfer of sensible heat as a rise or fall in the temperature of the air. Heat is initially transferred into the air by conduction as air molecules collide with those of the surface. As the air warms it circulates upwards via convection. Thus the transfer of sensible heat is accomplished in a two-step process. Because air is such a poor conductor of heat, it is convection that is the most efficient way of transferring sensible heat into the air.
When the surface is warmer than the air above, heat will be transferred upwards into the air as a positive sensible heat transfer. The transfer of heat raises the air's temperature but cools the surface. If the air is warmer than the surface, heat is transferred from the air to the surface creating a negative sensible heat transfer. If heat is transferred out of the air, the air cools and the surface warms. This situation may take place at night when the sun goes down and there is no input of solar radiation. At this time, the ground cools due to longwave emission and the air directly above the surface is warmer.
Latent Heat Transfer (LE)
When energy is added to water it will change states or phase. The phase change of a liquid to a gas is called evaporation. If we could see down to the molecular level we would find water being comprised of cluster of water molecules (H2O). The clusters are bound together by bonding between the hydrogen atoms of water molecules. The heat added during evaporation breaks the bonds between the clusters creating individual molecules that escape the surface as a gas. The heat used in the phase change from a liquid to a gas is called the latent heat of vaporization. We say it is "latent" because heat is being stored in the molecules. Water molecules release latent heat during the condensation process. We can't sense or feel latent heat as it does not raise the temperature of the water molecules.
When evaporation is taking place we say there is a positive latent heat flux (transfer). A positive latent heat flux (Figure \(\PageIndex{2}\)) is illustrated with an arrow pointing up away from the surface of the earth. This indicates that the surface is losing energy to the air above. Evaporation is a cooling process for a surface because energy is removed from the water as molecules escape the surface. This causes the surface temperature to decrease. You've probably experienced this cooling when water or sweat evaporates from your skin.

Condensation is the phase change from a gas to a liquid. During the phase change, the latent heat that was taken up during evaporation is released from the water molecule and passed into the surrounding air. During this process latent heat is converted to sensible heat causing an increase in the temperature of the air.
When radiation is absorbed by the Earth it will raise the temperature of the surface. But if the surface is water, some of that energy is used in evaporation rather than heating the water. As a result, with equal inputs of energy to land and water surfaces, land will heat up more than water. This is one of the reasons why it is cooler near large bodies of water.
Ground Heat Transfer (G)
The third major use of radiant energy is to warm the subsurface of the Earth. Heat is transferred from the surface downwards via conduction. Like in the case of sensible heat transfer, a temperature gradient must exist between the surface and the subsurface for heat transfer to occur. Heat is transferred downwards when the surface is warmer than the subsurface (positive ground heat flux). If the subsurface is warmer than the surface then heat is transferred upwards (negative ground heat flux).
The transfer of energy to and from the surface varies over the course of a day. Figure \(\PageIndex{4}\) shows the relative amounts and direction of energy flow during the day and night for a moist surface. During the day net radiation is a positive value as incoming radiation exceeds outgoing radiation allowing the surface to gain energy. The energy is distributed over the three major categories of energy use, LE, H, and G. During the day, the available radiant energy is used to evaporate water into the air, raising the air's humidity. Sensible heat is transferred upwards to warm the air above the surface. Heat is also conducted down into the subsurface. At night the processes reverse. At night with no incoming solar radiation there is more outgoing radiation than incoming creating a negative value for net radiation. Under these circumstances the surface cools due to a loss of energy and heat is transferred from the air toward the surface. As air cools through the evening the loss of energy allow condensation to occur, so long as the air's humidity is at or near saturation. Notice that the arrow for the ground heat flux G is pointing upward toward the surface. This indicates that the energy that had been stored in the subsurface during the day is now conducted toward the surface. This occurs as the surface is cooler than the subsurface.
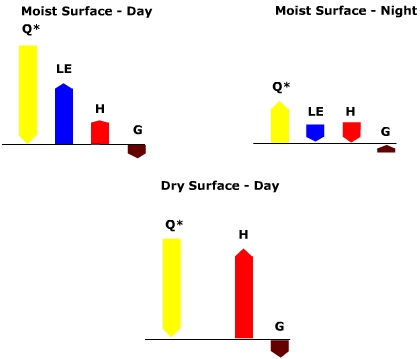
Figure \(\PageIndex{4}\) also shows the differences between how energy is used in moist and dry locations. Water is available at the surface for evaporation and latent heat transfer into the air at moist locations. Without available water, no transfer of latent energy occurs, hence the absence of an LE flux for the dry surface. Most of the available energy, Q*, is allocated to sensible heat transfer creating warm air temperatures.
Investigate more about the energy balance by "Digging Deeper: Local Energy Balances" or skip and continue reading.
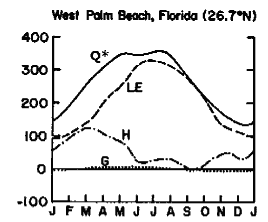
West Palm Beach, Florida is located in the warm and moist tropical wet and dry (savanna) climate. The annual variation of net radiation shows a typical pattern of Q* being at a maximum during the summer and minimum during the winter. Latent heat transfer (LE) is high at West Palm Beach because of the water availability near the ocean. Latent energy transfer into the air is greatest during the summer time which is the wettest period of the year, and when net radiation is the highest. Warmer summer time air can hold more moisture and hence there is a larger moisture gradient to drive latent heat transfer. The annual variation of sensible heat transfer is determined by the available net radiation and the temperature gradient between the air and surface, as well as use of energy for latent heat transfer. During the spring a larger temperature gradient exists between the surface and the air above. Ample rainfall occurs during the summer providing water for evaporation. During this time period, sensible heat transfer decreases as net radiation is allocated to evaporation and latent heat transfer.
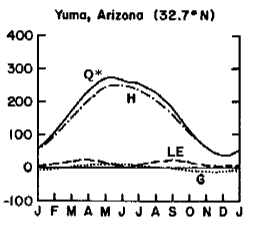
At the other extreme is Yuma, Arizona, a warm and dry location typical of the midlatitude desert climate. The most noticeable characteristic of this place is the lack of latent heat transfer. Though ample radiation is available here, there is little water to evaporate. Nearly all net radiation is used for sensible heat transfer which explains the hot, dry conditions at Yuma.
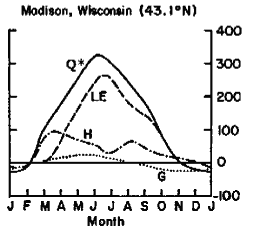
Between these extremes is Madison, WI found in the humid continental climate of North America. Latent heat transfer dominates for most of the year in this humid climate. Sensible heat transfer is especially high when surface and air temperatures are most different. The transfer of energy in and out of the subsurface is a much greater amplitude given that large temperature swings that are experienced in this climate.


