10.2: The Controls on Downslope Movement
- Page ID
- 13505
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Envisioning the Problem
At this point we need to take a closer look at what controls whether a mass of material will slide down a slope. Just to get your thinking started, here are two seemingly dissimilar but actually closely related situations:
- Making a pile of dry sand by pouring the sand slowly and continuously down toward the same point (Figure 8-2A)
- Placing a thick layer of soil on a horizontal sheet of plywood and then slowly tilting the sheet until some or all of the soil slides off (Figure 8- 2B)
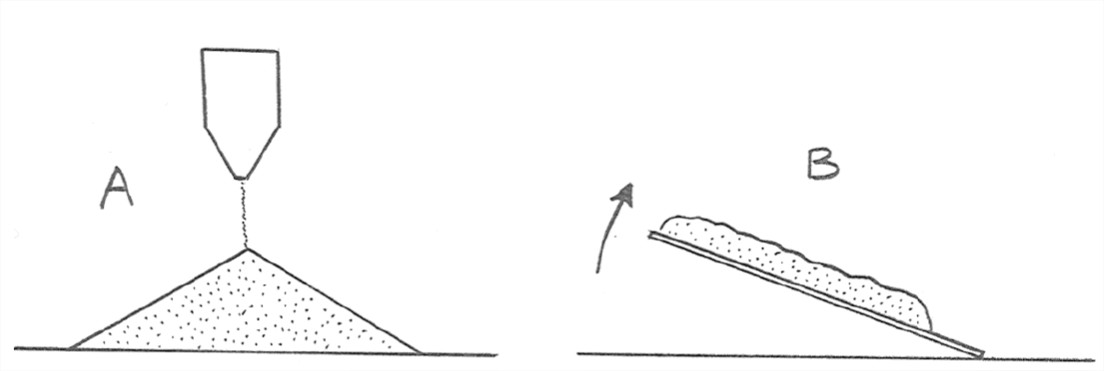
You must know, from your own experience, that when you try to build the sand pile in Figure 8-2A to have steeper slopes, a surface layer of sand suddenly slides down the slope, thereby decreasing the slope angle. As you build the pile to a larger and larger volume, the alternation of slope-increasing intervals and slope-decreasing intervals balances out, resulting in a constant average slope angle. That angle is called the angle of repose. For dry granular materials that are not extremely angular or jagged, the angle of repose lies in the range 30–35°.
Very angular blocks, of the kind that are common on talus slopes in mountainous areas, have greater angles of repose, but seldom more than 45°. (To me, such slopes always seem greater than they really are when I’m walking on them.)
As you gradually increase the slope of the plywood sheet in Figure 8-2B, at some point the whole mass slide off the sheet. (“Duh”, you’re probably thinking.) As a variant on the experiment, however, you might make the upper surface of the sheet ribbed or corrugated, with the ribs running in the transverse (horizontal) direction. How would that affect the value of the slope angle at which failure takes place?
Analyzing the Problem
In both of the situations described above, we need to think in terms of the force of gravity on a layer of material in the shape of a slab with its upper surface at the ground surface and its lower surface some depth below the surface (Figure 8-3). If the slab is stationary (not moving downslope), then there must be a friction force that’s exerted by the material underneath the slab on the material of the slab. We can place this imaginary plane anywhere in the material we want. Whenever and wherever the downslope gravity force exceeds the friction force, the slab above the plane slides downslope. We say that the material has failed along that plane. (The friction force we are dealing with here is the same as what I called the shear strength earlier in the course.)
BACKGROUND: FRICTION
Everybody knows about friction. Life without friction would be unbearable. Friction is essential for locomotion. We would all end up clumped together at the bottoms of local depressions in the land surface, unable to shift our positions in the least.
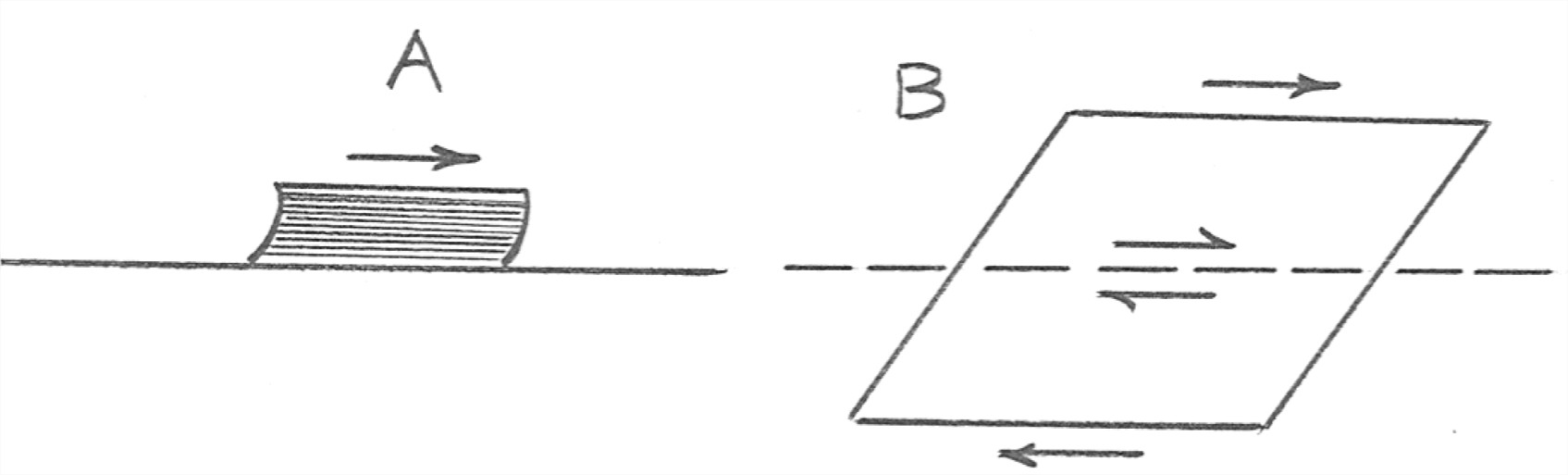
One instructive but technically incomplete definition of friction is that it’s the force that is generated when one mass of material slides past another mass of material with which it is in contact across a surface. That definition is a bit too specialized, because it doesn’t adequately cover the situation when a continuous medium, like water, undergoes a shearing deformation, as shown in Figure 10-4.
To get a handle on shearing deformation, think in terms of taking a thick telephone book and “racking” it so that the pages slide past one another, and then supposing that the shearing motion is continuous throughout, rather than page by page. In such shearing of a continuous medium, there is friction across any imaginary plane through the medium (Figure 10-4B).
The phenomena of friction are messy. They involve the details of the surface along which the friction force acts, on scale ranging from macroscopic bumps and corrugations down to the atomic scale. Only recently have physicists begun to inquire deeply into the nature of friction.
Friction can be dealt with by gathering or subsuming all of the messy phenomena into a single coefficient. (The fancy general term for that kind of thing is called parameterizing.) Figure 8-5 shows a slab being made to slide on a horizontal surface by exerting a horizontal force on it. When the slab is moving at constant speed, the force that needs to be exerted on the slab to keep it moving is equal to the friction force between the bottom of the slab and the underlying surface.
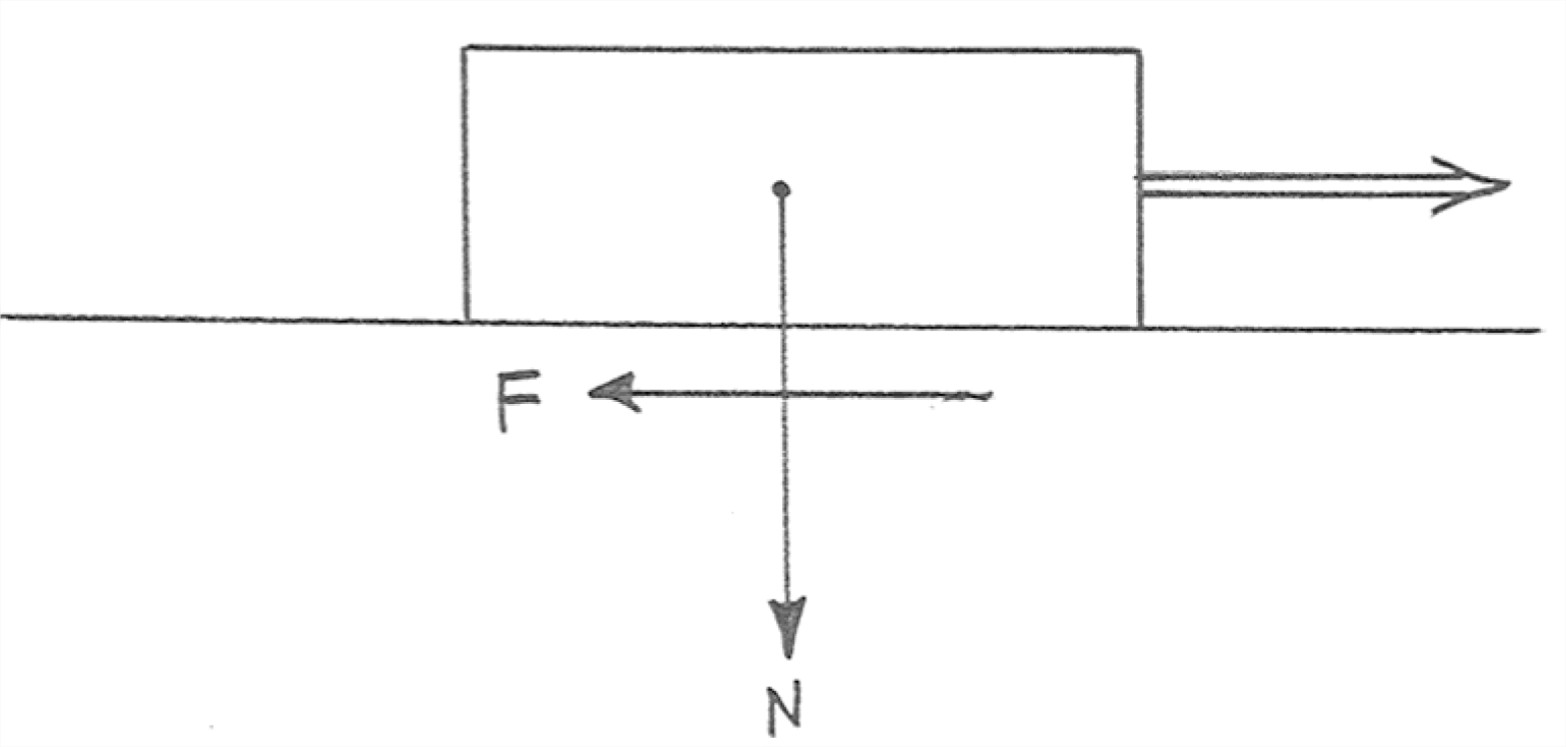
Let the weight of the slab, per unit horizontal area, be N, and the friction force, again per unit area of contact between the slab and the underlying surface, be F (Figure 10-5). These two quantities, N and F, are related by the equation F = μN, where μ is called the coefficient of sliding friction. It depends only on the nature of the surfaces in contact. Its value is usually less than one. There’s an analogous coefficient for static friction, in the situation where the force that tends to move the slab is not yet big enough to cause the slab to move. The coefficient of static friction is generally larger than the coefficient of sliding friction.
If you run the experiment on sliding of a layer of material down your sheet of plywood, you would find that the failure plane (the plane where sliding is located) is always at the bottom of the layer of material, whether or not the surface of the plywood is smooth or corrugated. It’s easy to see why. The downslope driving force (the weight of the material above a given plane parallel to the plywood sheet) increases with the thickness of the material above that plane, but the coefficient of friction is the same throughout the material. The shear strength of the material (or, what is the same, the static friction) is therefore overcome first at the deepest plane in the layer.
The situation with your sand pile is a bit different. What’s happening there is that the slope is oversteepened at the tippity-top of the pile, as a lobe of new material is built. Eventually the lobe fails, and its material slides down the slope.
The Real World
Now, with all of the foregoing material on the downslope pull of gravity, the nature of friction, and the shear strength of materials as background let’s think about slope failure in nature. The problem is easy to state. In most places, the land surface has some slope angle. That leads to the possibility of failure and sliding of material downslope. That’s the essence of mass wasting. Most of the time, of course, the stuff just sits there on the slope, not moving. (But I will be amending that seemingly obvious statement, in a very important respect, in a later section.) At certain times and places, however, failure occurs, and there is sudden downslope movement, often fast, of some volume of material, often large. What are the factors that determine when and where that will happen? There are two aspects that are important to think about:
- What might cause previously stationary material on a slope to be mobilized?
- How deep below the surface will the failure plane be located?
Let’s address the second question first. In nature, with its layer of regolith and weathered rock at the surface and solid bedrock, with its greater strength below, the depth at which failure first occurs depends on the competition between two effects: the tendency, discussed above, for failure to occur as deep as possible; and the general tendency for the shear strength of the material to increase, usually greatly, downward in the transition from regolith to bedrock.
The first question is more difficult to address. Several things, all of them important, might cause failure:
- The material on the slope might be loaded from above, by addition of new layers of material. If there is no concomitant increase in the shear strength of the underlying material, that might lead to failure.
- The slope might be steepened by differential deposition, whereby a layer of newly deposited material is thicker high up on the slope than low down on the slope. That increases the downslope component of the gravity force on the material.
- The base of the slope might be undercut, by stream erosion, for example.
- The shear strength along some plane in the material might be lowered by some effect.
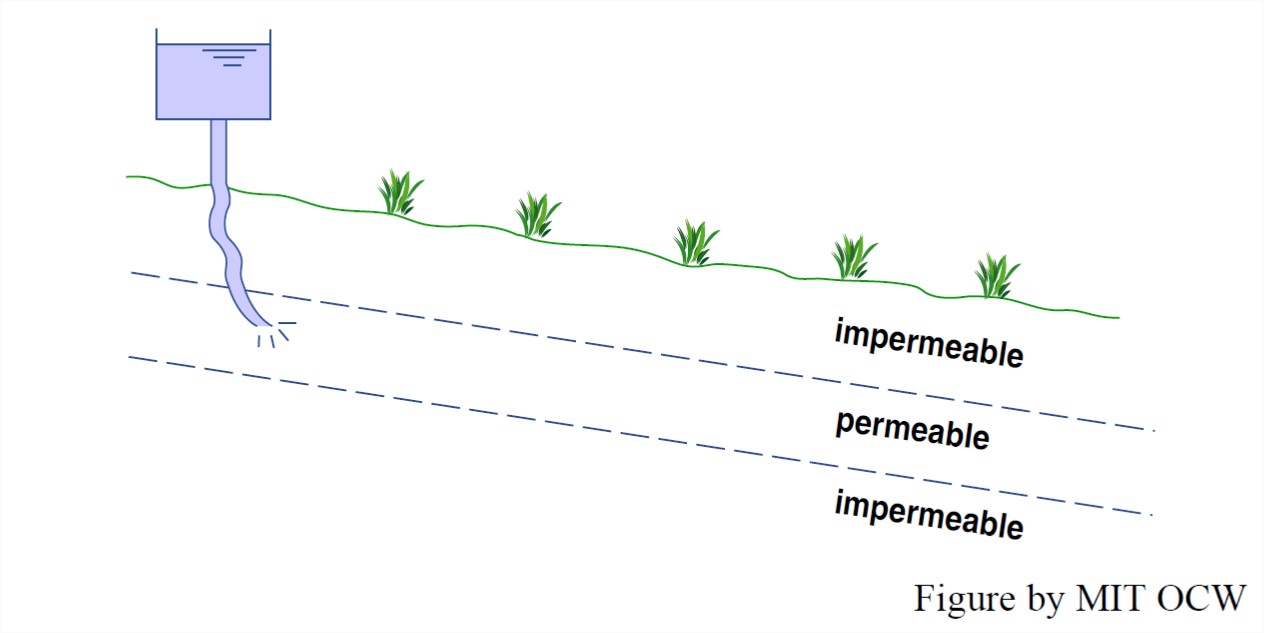
The last of these calls for further comment. The shear strength of a granular material like regolith, as well as a solid but porous material like sedimentary rock, arises from the particle-to-particle forces. If that force can be decreased somehow, the shear strength is lessened. A good way to do that is to increase the pore pressure in the layer. (By pore pressure, I mean the water pressure of the water in the connected pore spaces in the material.) Figure 10-6 shows this effect, in a very schematic way. Suppose that there is a layer of relatively permeable material that lies between an overlying layer and an underlying layer of effectively impermeable material. If in some way the fluid pressure in the permeable middle layer is pumped up, that extra pressure tends to lift up the overlying material, thus relieving some of the particle-to-particle forces and lowering the shear strength. That’s conducive to failure, and sliding of the overlying layer downslope.