10.1: Introduction to Mass Wasting
- Page ID
- 13504
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Everything at or near the surface of the Earth is pulled toward the Earth by the force of gravity. (“Gravity: it’s a law you can live with.”) That includes all Earth materials, rock and regolith. This is one of the central concepts of this course. Its importance lies in the fact that under certain circumstances those materials are moved downslope by the pull of gravity. Processes of downslope movement of surficial Earth materials under the pull of gravity are collectively termed mass wasting. (I’ve always thought that term to be rather infelicitous, but there it is.) This is a good time to look at the two background sections on gravity at the end of this section.
You might view the problem of mass wasting in terms of an atrocious paraphrase of a famous quotation: “To move downslope, or not to move downslope?” The criteria for initiation of downslope movement of Earth materials by gravity are not straightforward, but they are of great practical as well as theoretical importance: mass-wasting events are responsible for enormous loss of life.
Processes of mass wasting are highly varied in three important respects:
- mass of material involved
- speed of movement
- nature of movement
Masses of material vary from tiny mineral grains tumbling downslope to enormous masses with volumes of rock and mineral material as great as thousands of cubic kilometers. (Yes, thousands; that’s not a typo.) Speeds range from imperceptibly slow, less than a meter per year, to hundreds of meters per second. The nature of movement ranges from intact masses, which retain their original structure, to those that become thoroughly mixed and homogenized during the movement. Given this wide range of characteristics, it should not come as a surprise to you that classification is difficult and terminology can be confusing.
BACKGROUND: GRAVITY
Everybody knows about gravity. For the sake of clarity, though, here’s some background material on it.
First of all, there’s a distinction between gravitation and gravity. Gravitation is the more general concept: it’s an attraction between any two bodies of matter in the universe. As with many important things in physics, it began with Newton: he formulated what is now called Newton’s law of universal gravitation, that any two bodies of matter exert an attractive force upon each other that’s proportional to the product of their masses and inversely proportional to the square of the distance between them. (It’s one of a number of manifestations of what physicists call “inverse-square laws”.) Does it surprise you to learn that gravitation is an extremely weak force? It gets big only when one or both of the bodies is very massive, like stars or planets.
The Earth exerts a force of gravitational attraction upon us, and upon everything else on Earth as well. That’s what’s called the force of gravity. (We exert an equal and opposite force on the Earth, but we usually don’t bother to think about that. It probably seems ridiculous to you to think that each of us exerts that big force on the whole Earth, but it’s true.)
What we call weight is just the force of gravity the Earth exerts on us or on other bodies of matter. It’s important to be clear on the distinction between mass and weight. The mass of a body is a measure of the amount of matter of which that body is composed; the weight of a body is the force of gravity the Earth (or any other solar-system body, for that matter) exerts on the body. That’s why the astronauts weighed so much less when they were on the Moon, and why astronauts in deep space are weightless, even though they are not massless.
BACKGROUND: THE DOWNSLOPE COMPONENT OF GRAVITY
The force of gravity that the Earth exerts on us is directed toward the Earth’s center of mass—which is almost identical to the Earth’s center of volume. (It’s just generally called “the center of the Earth”.) The way “horizontal” is defined, anywhere on Earth, is just the plane that’s perpendicular to the direction of the force of gravity, at that locality. Any still water surface is coincident with that horizontal plane—because if the surface were not horizontal, it would be sloping, and gravity would pull the water down the slope until no slope remains.
That leads us directly to the important idea that the force of gravity can be viewed as having a part that acts in all directions that are not coincident with the horizontal plane. That force is called the component of the force of gravity in that particular direction. To deal with that quantitatively, you need to know something about the mathematics of vectors. (A vector is a quantity that has both magnitude and direction, and behaves according to a particular set of rules; no details here.) You can resolve a vector into components along any set of axes, by certain mathematical rules.
Figure 8-1 shows how the force of gravity of a body resting on a sloping surface can be resolved into two components, one parallel to the surface and one perpendicular to it. What I want you to see in this is that the downslope component of gravity gets smaller as the slope gets gentler: it varies from the full force of gravity, in the vertically downward direction, to zero, on a horizontal, surface.
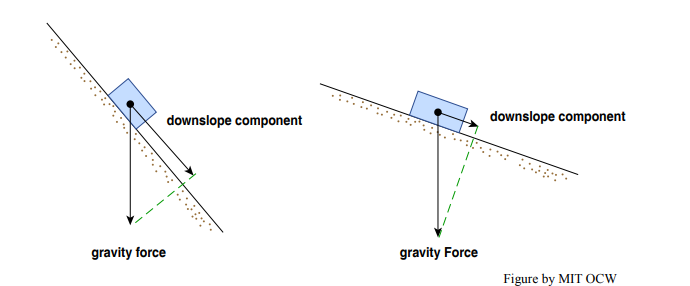
All of this should make good qualitative sense to you, because it’s part of the human experience: we are pulled down a steep slope more than down a gentle slope. The same is true of all rock and regolith on the Earth’s surface as well, and that’s what’s important for this chapter.


