9.4: Saltation

Earlier in the course I tried to give you a qualitative picture of the nature of sediment movement by flows of water. You learned that sediment is moved by water as bed load and as suspended load. The picture of sediment transport by air is somewhat different. This is basically because the ratio of sediment density to fluid density is almost three orders of magnitude greater in air than in water. This means that once a sediment particle is set in motion by a flow of air, the particle tends to follow a trajectory that is largely independent of the details of turbulence in the air, because of the great relative inertia of the particle. In water, on the other hand, sediment particles in transport tend to follow rather closely the patterns of motion in the water itself.

The forces the wind exerts on sediment particles resting on the land surface are not greatly different from those exerted by flowing water, and particles can be set into motion as bed load or lifted into suspension, just as in flowing water. But particles of sand size or greater, which are set into motion as bed load, are able to make much stronger impacts with the sediment surface, because of the relatively slight cushioning effect of the fluid. The consequence is far greater importance of ballistic or collisional effects in eolian transport. This is manifested in a characteristic mode of transport called saltation.

The term saltation is used for a mode of particle movement in which trajectories of particles show take-off from the bed at moderate to steep angles and descent to the bed at small angles. Figure \(\PageIndex{1}\) shows a typical saltation trajectory taken by a saltating grain of sand in air. Saltation trajectories are rather regular, and then they show little of the sinuosity that might be expected from passage through turbulent eddies. This is because of the typically large ratio of particle density to fluid density: the particles have great relative inertia, and they can cruise almost unaffected through eddies with rather different local fluid velocities.

Figure \(\PageIndex{1}\): A typical saltation trajectory of a sand particle moved by the wind.

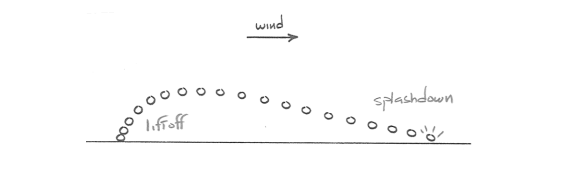
Saltation is the dominant mode of particle movement when a strong wind blows over a sand surface. Except in the very strongest winds, the saltation heights attained by the saltating grains seldom exceeds a meter, and the saltation lengths are mostly less than a few meters. There is, of course, a continuous distribution of jump heights and jump lengths, from zero to the maximum. There’s also wide variability in take-off angles: they range from just a few tens of degrees to vertical. After colliding with some particularly immovable bed grains, some saltating grains even take off with an upstream component to their motion!

If you are lucky enough to be out on a dry sand surface during a strong wind, take the risk of getting some sand in your eyes and nose and mouth, and get down for a horizontal view at an eye level of a few tens of centimeters above the surface. You would see a hazy layer of saltating grains, which tails off imperceptibly upward. This well defined layer of saltating grains is called the saltation carpet. If you then looked downward at the sand surface, you woul see an abundance of surface grains being pushed and jogged along for short distances, just one or a few grain diameters at a time, presumably by being struck by saltating grains. That mode of movement is called surface creep—but there is actually no sharp break between surface creep and saltation.

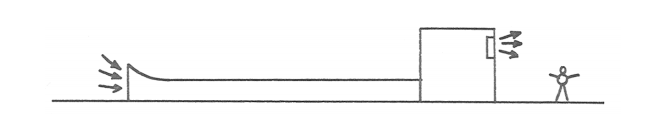
To see individual saltation trajectories nicely you would have to be out there at night with a strobe light. The best thing to do is shine the strobe light straight down at the bed through a horizontal slit oriented parallel to flow; that way you see only a thin slice of the saltation carpet. The effect is striking. You could easily do the same thing in a homemade wind tunnel, which doesn’t have to 418 be any bigger than tabletop size. The most common kind of wind tunnel for studies of sand movement (Figure 9-2) consists of a duct with a flared entrance, which passes into a large collection box with an exhaust fan on the other wall. You can start with the sand in the duct, or you can shower it into the upstream end through a slit in the roof of the duct.

Figure \(\PageIndex{2}\): A wind tunnel of suction type.

Many aspects of saltation are not well understood. Among these is the mechanism that causes the initial rise of the grains. Two different effects might be important:

Aerodynamic lift forces

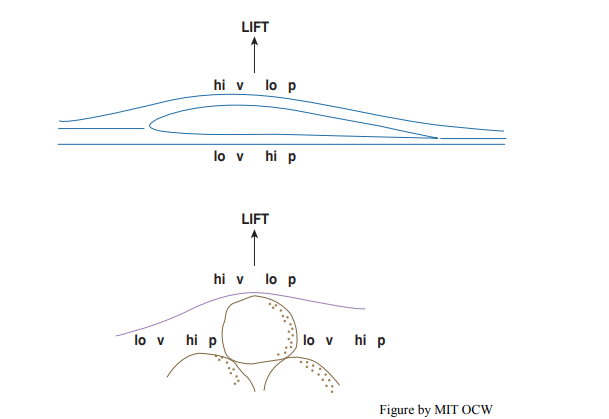
This is not the place to discuss the intricacies of the Bernoulli equation, which expresses the relationship between fluid pressure and fluid velocity in any flowing fluid. Suffice it to say that along any flow line in the flow there is an inverse relationship between the pressure and the velocity: where the velocity is high, the pressure tends to be low, and where the velocity is low, the pressure tends to be high. This is what makes airplanes fly (Figure \(\PageIndex{3A}\)): the shape of the wing section is such that the air travels a shorter distance around the lower surface of the wing than around the upper surface, so the velocity is lower and the pressure is higher. This pressure difference between the lower surface and the upper surface of the wing is called lift. The same is true of a sand particle resting on a sediment surface (Figure \(\PageIndex{3B}\)): the velocity is relatively low around the base of the particle and relatively high at its top, so there is a net upward pressure force in addition to the downwind drag of the wind. Ballistic collisions between the moving particle and the bed particles. When a flying particle makes impact with the bed, it imparts part of its momentum to one or more bed particles. One or more of the bed particles is likely thereby to be launched into motion above the bed. Take-off velocities and angles depend in some very complicated way upon the local geometry of arrangement of the bed grains and upon the velocity and location of impact.

Despite much research over the years, the relative importance of these two effects—aerodynamic lift and particle collisions—is still controversial.

Figure \(\PageIndex{3}\): Aerodynamic lift forces. A) On an airplane wing. B) On a sediment particle.

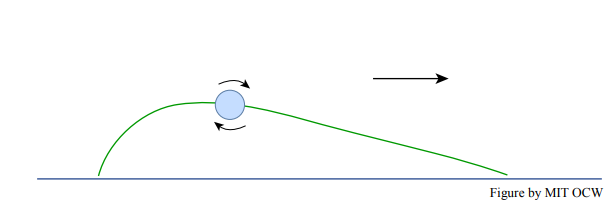
An interesting aerodynamic aspect to saltation has to do with the rotation rates of saltating particles. Ultra-high-speed motion pictures have revealed strikingly high spin rates of hundreds of revolutions per second. The sense of spin is such that that the top of the particle moves faster in the downstream direction than the bottom of the particle (Figure \(\PageIndex{4}\)). The origin of such high rates of spin is still a mystery. But it’s clear that the spinning motion gives rise to a non-negligible additional lift force on the particle, by what’s known as the Magnus effect: the rotation of the grain alters the streamline pattern around it in such a way that instead of the pattern being symmetrical about the grain, the streamlines are closer together above the grain than below it (Figure \(\PageIndex{5}\)). By the Bernoulli equation, this means that the fluid pressure at the grain surface is smaller above the grain than below, causing a net lift force. It’s the same effect that makes for curve balls, and for those annoying slices and hooks.

Figure \(\PageIndex{4}\): The sense of rotation of a saltating particle.

Figure \(\PageIndex{1}\): The Magnus effect

Except in the very strongest of winds, saltating sand grains seldom attain heights greater than somewhere between one and two meters. So the Hollywood conception of a sand storm, in which the protagonist steps out of his tent into a blinding, choking cloud, is all wrong: in a real sand storm the air at one’s eye level is clear, but one’s legs are being bombarded by zillions of saltating sand grains. Hollywood sand storms are really dust storms, which can happen only where there’s not only a strong wind but also a freshly available surficial layer of fine sediment, as from a recent flow of water after a heavy rain. Dust storms aren’t very common in deserts, because these fresh supplies of sediment are made available to the wind so infrequently.