8.4: Beaches

Shoaling Waves

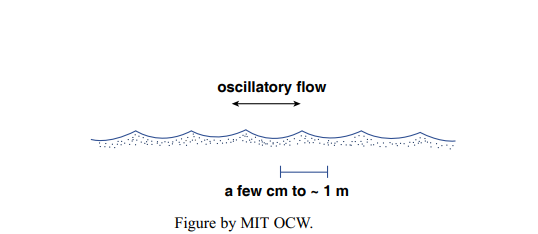
First go back to Chapter 1 and review the material on surface gravity waves. Now it’s time to think about what happens to a train of waves propagating from the deep ocean to the shoreline. The waves start as deep-water waves, but as they shoal the begin to “feel the bottom”, in the sense that they make the water move at the bottom. This bottom friction causes some loss of wave energy. Also, if the orbital velocity of the water at the bottom becomes great enough to move sand, oscillation ripples (a kind of oscillatory-flow bed configuration) develop (Figure 8-25).

One of the most important effects connected with shoaling waves is that they slow down. It turns out that for shallow-water waves the wave speed c is proportional to the square root of the water depth. Because the wave period itself doesn’t change (the waves keep on being supplied from offshore at the same period), by the relation L = cT the wavelength decreases. Wave height H also increases, for reasons connected with conservation of wave energy that are too complicated to discuss here, and the combined effect leads to increase in wave steepness. This can’t go on indefinitely (the limiting steepness H/L turns out to be one-seventh), so eventually the waves fall over on themselves, or in other words they break.

Figure 8-23. The tidal-current rose measured at the Nantucket Lightship.

Figure 8-24. An example of a more elongated tidal-current rose.

Figure 8-25. Oscillation ripples.

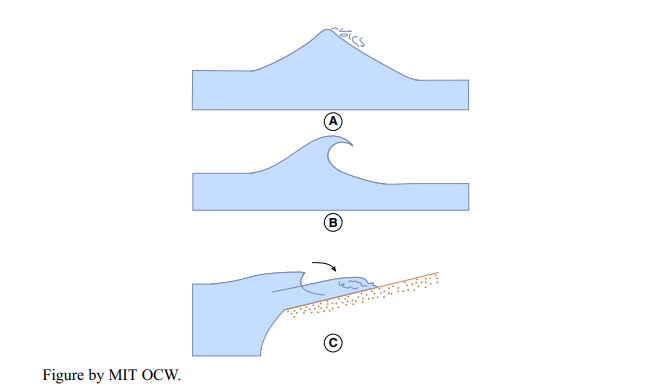
The form taken by the breaking waves depends on the rate of change in the steepness as the waves shoal. Three types of breakers are generally recognized (but keep in mind that there’s a gradation among them):

spilling breakers: the wave peaks up slowly, the crest becomes unstable and spills down the front surface of the wave, and the wave height slowly decreases (Figure 6-26A). These tend to occur with gentle bottom slope and originally steep waves.

plunging breakers: the wave peaks up rapidly, and the crest becomes a thin vertical wall that curls over forward and then plunges forward and downward, causing a catastrophic decrease in wave height (Figure 6-26B). These tend to occur with steep bottom slope and originally intermediate-steepness waves.

surging breakers: the wave peaks as if to plunge, then the base of the wave surges up the beach face, and the crest collapses and disappears (Figure 8-26C). These tend to occur with very steep beaches and originally low-steepness waves.

After the wave has broken, the water rushes up the beach as a moving mass, which can be thought of as a wave of translation (in contrast to former nature of the wave, wherein the water had no net translation). This called the swash. The water carried up the beach as swash returns under the downslope pull of gravity as backwash.

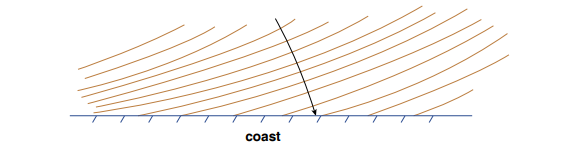
Another effect of the slowing of waves as they shoal is refraction. You may have noticed that waves moving toward shore tend to curve around so as to be more nearly parallel to the shore (Figure 8-27). This is an inevitable consequence of the slowing of the waves as they move into shallower water. Here’s an easily understandable analogy. The drill sergeant is putting a squad of marching persons through their exercises. At one point he/she tells the people on the left to take baby steps and the people on the right to take giant steps. You can easily envision what will happen: the direction of movement of the squad will curve around to the left. This is exactly the same refractive effect that makes the shoaling waves swing around to be more nearly parallel to the shoreline.

Figure 8-26. Varieties of breaking waves. A) Spilling breakers. B) Plunging breakers. C) Surging breakers.

Figure 8-27. Refraction of waves as they shoal toward a shoreline.

Beach Profiles

It’s easy to define a beach. A beach is a mass of non-cohesive sediment along a shoreline that’s molded by wave action. The sediment size of beaches ranges from the finest sand to coarse gravel. The best way to approach the dynamics of beaches is to look at a vertical cross section normal to the shoreline; such a cross section is called the beach profile.

To establish some terminology, Figure 8-28 is a sketch of a representative beach profile. I want to emphasize that beach profiles vary a lot in their geometry and in the kinds of features they show—both from beach to beach and at the same beach as a function of time. The sketch in Figure 8-28 is a typical snapshot, but it’s not representative of all beaches.

Figure 8-28. Shore-normal vertical profile through a beach.

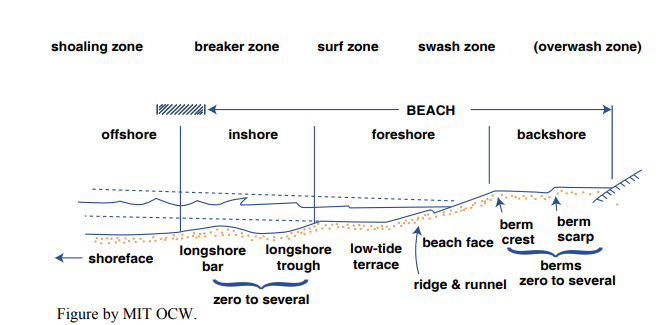
(The seaward limit of the beach is a matter of definition; depending upon who’s doing the defining, it can range from mean low tide to the seaward limit of breaking waves, which can be much farther offshore.)

Some general points about this profile:

• As discussed in the section on shoaling waves above, the strength and nature of bottom-water movements associated with breaking waves vary greatly and systematically from deep water to land.

• The beach profile is always changing with time, in an effort to keep up with the ever-changing wave state. We naturally assume that for each given wave state and beach sediment there’s an equilibrium profile, in the sense that, whatever the initial geometry of the beach, the final equilibrium geometry attained by the beach after prolonged exposure to that wave state is the same. But because in the real world the wave state changes all the time, the beach is always adjusting toward a new equilibrium.

• The nature of sediment movement on the beach varies not only with the waves but also with the sediment size, which itself depends in a complex way on the long-term average wave state and on the nature of sediment supply to the beach.

Onshore–Offshore Transport

The main feature of sediment movement on the beach is the back- and-forth movement of the sand in response to the swash and backwash of the waves. Sand is carried up the beach as both bed load and suspended load by the relatively deep and strongly turbulent swash, and it’s carried back down the beach mostly as bed load by the thinner and less turbulent backwash.

For a given beach sand, the vertical profile of the beach is very sensitive to wave conditions. At any given time there’s nearly a balance between sand moved up the beach by the swash and sand moved down the beach by the backwash. The volume of backwash is always smaller than the volume of swash, because water percolates into the porous beach sand. To maintain the balance in upslope and downslope sand movement, the beach takes on a particular slope so that the force of gravity hinders upslope transport by the swash but aids downslope transport by the backwash.

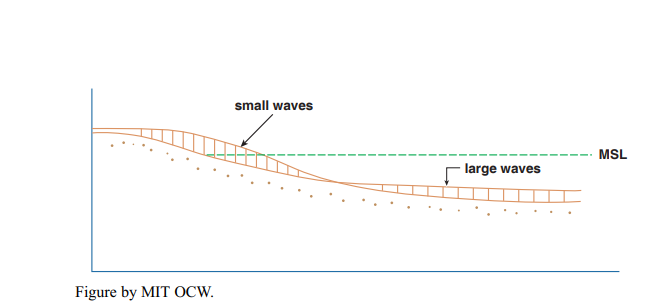
What’s therefore important in governing the slope of the upper part of the beach is the ratio of backwash volume to swash volume. As wave height increases, the volume of water moving up and down the beach increases, but because the volume lost by percolation doesn’t increase very greatly the percentage of backwash compared to swash is greater than for waves with low steepness. So more material is moved down the beach, and the slope on the upper part of the beach decreases. The sand thus eroded from the upper part of the beach is parked farther offshore, although still within the beach system. During periods of good weather, with smaller waves, the ratio of backwash volume to swash volume decreases, and the slope of the upper part of the beach increases again, as sand is supplied from offshore. Figure 6-29 shows beach two profiles, one for small waves and one for large waves.

Ordinarily the sand that’s parked offshore during periods of strong waves isn’t lost to the beach system, and it’s moved back onto the upper part of the beach—the part we see and lie on and play on—during periods of weaker waves. Only during unusually large storms can there sometimes be mobilization of great masses of sand and transport farther out to sea.

Figure 8-29. Beach profiles for times with small waves and times with large waves.

By much the same line of reasoning, the slope of the beach varies directly with sand size: coarser beaches admit of greater percolation, so for a given wave state the beach has to be steeper to strike the balance between upslope and downslope sediment movement. Beaches with fine sand have very gentle slopes, sometimes of only a few degrees. Such beaches can be hundreds of meters wide. On the other hand, beaches formed of coarse gravel in areas exposed to very strong waves can be as steep as the angle of repose of the gravel, well over 30°. (The angle of repose is the slope angle that’s assumed by apile of loose sediment that’s formed by pouring the sediment from a point above the pile.) On such beaches there’s no backwash: the water of the swash percolates so rapidly into the beach that there’s none left to flow back down the beach as backwash! Then the downslope pull of gravity is the only thing that counteracts the upward transport by the swash.

Longshore Transport

So far I’ve talked only about sediment movement in the onshore– offshore direction. Sand is also moved along the beach, in various ways. Such movement is called longshore transport, or littoral drift, or longshore drift.

How is longshore transport observed? It’s notoriously difficult to make direct measurements of sediment transport rate, especially in complicated situations like beaches, where various kinds of water movements are superimposed upon one another, but two lines of indirect evidence should be readily understandable:

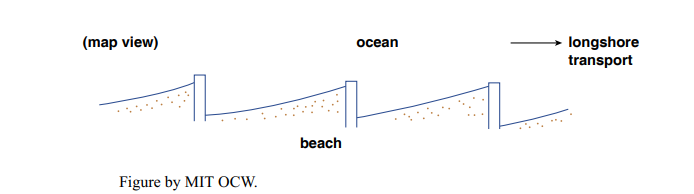
• piling up of sand in front of groins and jetties, and depletion behind them (Figure 8-30);

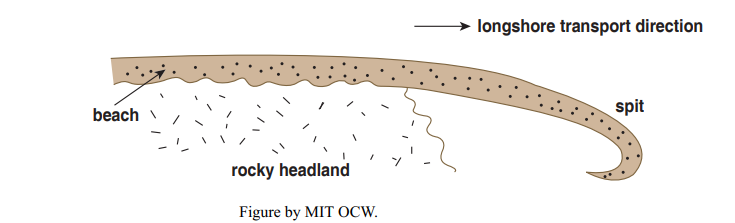
• building of sand spits at headlands (Figure 8-31).

Figure 8-30. How sand piles up a the updrift sides of groins.

Figure 8-31. A sand spit at a headland.

Another good line of evidence, less obvious to the casual observer, is the presence of distinctive sediment along the beach downdrift from the mouth of a river (Figure 8-32).

Finally, you can imagine marking or tagging a small volume of sediment, with paint or even with a radioactive coating, and then looking for it in the downdrift direction after some period of time. That’s an excellent way of getting qualitative information on longshore transport. But getting actual rates of movement, in terms of mass of sand moved per unit time, is much more difficult, largely because of problems connected with mixing of the marked sand downward into the underlying sand.

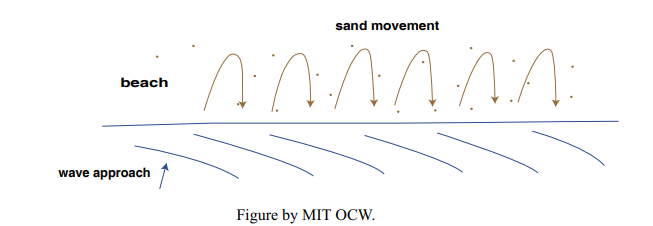
Longshore transport is complicated, because several different mechanisms contribute to it. One kind of longshore transport, called beach drifting, is easy to understand: it comes about because the waves approach the beach obliquely rather than straight on. (It’s generally the case that waves don’t approach the beach straight on.)

Figure 8-32. Downdrift movement of a tracer introduced to the coastline by a stream.

Despite the tendency for wave refraction to make the waves more nearly parallel to shore, waves still tend to be slightly oblique to shore when they break (Figure 8-27). So the swash (the wave of translation produced by breaking) runs not straight up the beach but diagonally, moving sand diagonally with it. As the swash loses its momentum and is pulled back down the beach by gravity, it flows more nearly straight down the beach, again carrying some sand with it. The net effect on the sand is to be displaced slightly down the beach in sawtooth fashion, in the direction of wave approach to shore (Figure 8-33).

Figure 8-33. Beach drifting.

The other important cause of longshore transport is the presence, immediately adjacent to the shoreline, of a steady current flowing parallel to the beach. Such a current is called a longshore current. The causes of longshore currents are varied. Here are three possibilities:

• the sawtooth movement of swash and backwash by obliquely approaching waves, described above;

• currents caused by complex processes associated with the oblique approach of the waves themselves;

• currents present in the nearshore zone but not caused by wave shoaling.

Whatever their origin, longshore currents can transport sand just like currents in a river. In fact, the ability of longshore currents to transport sand is enhanced by the suspension of sand by breaking waves in the breaker zone: there can be appreciable longshore transport by longshore currents even though the currents are not strong enough to move the sand by themselves.

Beach erosion is much in the news, especially in southern New England and on Long Island. The best way to think about beach erosion is in terms of the budget of sand involved in longshore transport, because we’ve seen already that little sand is lost to the beach by direct offshore movement. In this view, beach erosion in one locality is offset by beach deposition somewhere else. In areas where less sand is supplied from upstream than is transported downstream there’s beach erosion, and the position of the beach moves landward; in areas where more sand is supplied from upstream than is transported downstream, there’s beach deposition, and the position of the beach moves seaward.

In the context of Cape Cod or Long Island, you have to keep in mind that they are basically just gigantic piles of coarse sediment that were parked there while the terminus of the last continental ice sheet stayed in about the same place for a long time at the height of advance of the ice sheet, and after sea level rose to about its present position those piles of sediment have been exposed to wave action and longshore transport without any new source of sand, as from a major river system. So the only source of sand for the inevitable longshore transport comes from the beach itself, and the sediment cliffs behind the beach. On the other hand, lots of new beach is being built by longshore transport to the “downstream ends” of the beaches—Provincetown and Monomoy, in the case of Cape Cod.

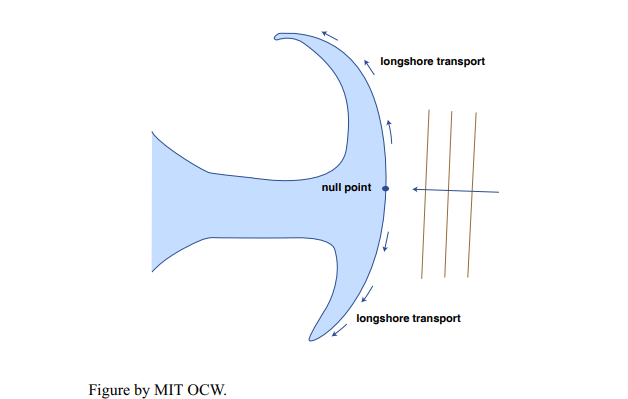
Figure 8-34 is a sketch of outer Cape Cod, showing the direction of approach of the dominant sand-moving waves and the net longshore transport directions. South of a point about in the middle of the face of the outer Cape, net longshore transport is to the south, and north of that point, net longshore transport is to the north. The dividing point is called a null point. For a long distance north and south of the null point there’s net erosion of the beach. But to the north and south of that zone of net erosion, there’s net deposition, as the spits extend themselves ever farther.

Figure 8-34. Longshore transport along the outer face of Cape Cod.