5.10: Drainage Networks
- Page ID
- 14319
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
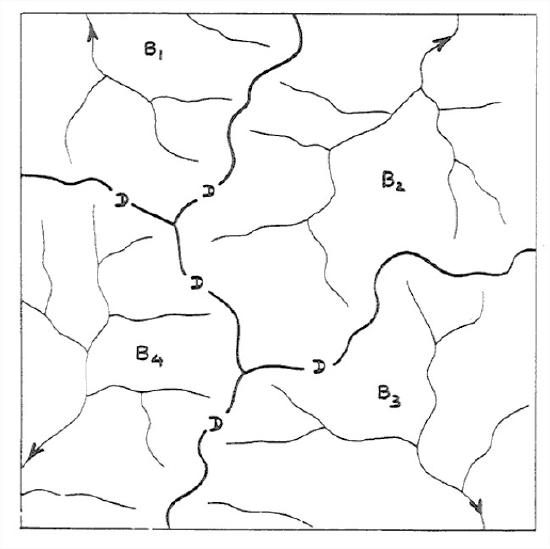
Given an area of land on which rain falls, there are always streams, even if they are only ephemeral. The entire area can be parceled exhaustively and mutually exclusively into sub-areas such that each sub-area is the drainage area of a single stream (Figure 5-42). Such areas are called the drainage basins or watersheds or catchments of those streams. You learned some things about drainage basins in the earlier chapter on topography. Recall from Chapter 3 that the boundaries between adjacent drainage basins are called divides. Just think of standing straddling the divide and pouring a glass of water from one hand into one drainage basin and from the other hand into the other drainage basin. Here the emphasis is on the network of streams in the drainage basin. The drainage network of a drainage basin is the collection of all of the channels in a given drainage basin: the main stream, often called the trunk stream, and all of the tributaries, as well as the tributaries of tributaries, and so on.
Drainage Patterns
By drainage pattern I mean the spatial relationships of individual streams in the drainage basin. The drainage pattern is a reflection of several factors:
- stage of development
- initial slope
- rock hardness
- rock structure
- recent tectonism
The pattern of each of the drainage networks shown in Figure 5-41 is what you would expect to see in a region that is underlain by fairly uniform materials—that is, materials that are about the same in their characteristics, in particular their susceptibility to erosion, from place to place.
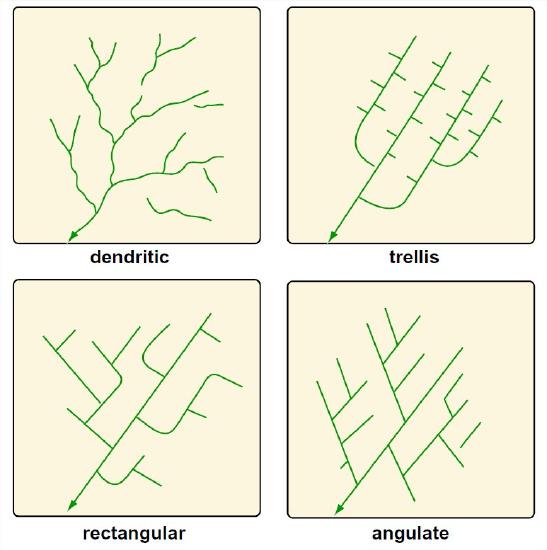
Because an area responds to denudation (by denudation I mean lowering of the land surface by weathering, erosion, and removal of the resulting regolith) in a way that reflects the underlying geology, you can tell a lot about the geology of an area by looking at a map of the drainage pattern. Here are some of the common drainage patterns (Figure 5-43), with a few words on the bedrock controls:
Dendritic. This pattern, by far the most common, involves irregular branching of tributary streams in many directions and at almost any angle, though usually less than 90°. A dendritic pattern develops on rocks of uniform resistance, and without structural control. It is most likely to be found on flat-lying sedimentary rocks or massive igneous rocks. The drainage networks shown in Figure 5-41 could be described as dendritic.
Trellis. A system of subparallel streams, usually aligned along the strike of rock formations or between parallel or nearly parallel topographic features deposited by wind or ice. The main streams often make nearly right-angle bends to cross major ridges. The primary tributary streams are usually at right angles to the main stream, and the secondary tributaries are usually themselves at right angles to the primary tributaries, i.e., parallel to the main streams. Trellis patterns are most common in folded mountain belts like the Appalachians, where alternating folded weak and strong layers have been truncated by stream erosion.
Rectangular. Both the main stream and its tributaries show right-angle bends. This reflects control exerted by joint or fault systems. Where the joint or fault systems intersect at acute angles, an angulate pattern develops.
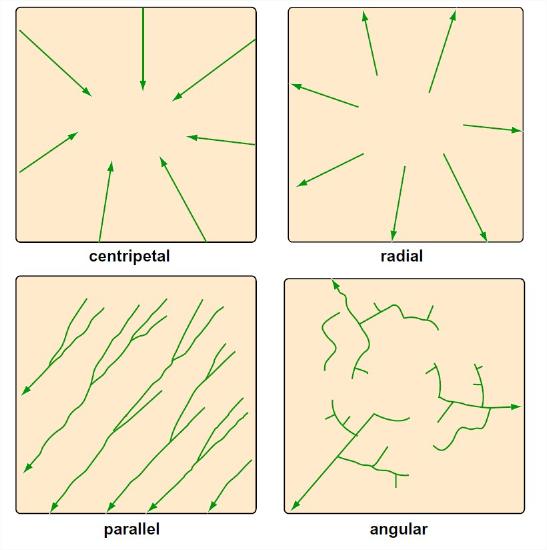
Some other patterns (Figure 5-44) are less common:
- Centripetal. Drainage lines converge into a central depression, like a sinkhole, crater, or other basin.
- Radial. Streams diverge from a central elevated tract: domes, volcanic cones, isolated conical hills.
- Parallel. Found where there is a strong slope control, leading to regular spacing of parallel or nearly parallel streams.
- Angular. Around maturely dissected domes which have alternating belts of strong and weak rock around them.
ADVANCED TOPIC: FLUVIAL MORPHOMETRY
Fluvial morphometry is the term used to describe the analysis of the topological characteristics of drainage networks..
Here are some things you could measure about a drainage network:
• configuration or topological properties
• linear properties: analysis of a branching system of one-dimensional curves in plan.
• areal properties: analysis of areas of drainage basins, again in plan.
• relief properties: analysis of slope of channels or drainage areas.
Each one of these properties has been subjected to extensive study by the techniques discussed below. We’ll examine only the first here.
First we need to define the concept of the order of a stream. To do that, look at a representative drainage network, and concentrate on its topology. The stream-channel network can be subdivided into segments lying between confluences, together with fingertip streams lying upstream of any confluences (Figure 5-45). One can develop a hierarchy of stream orders based on the tributary relationships of the channels, in the following way.
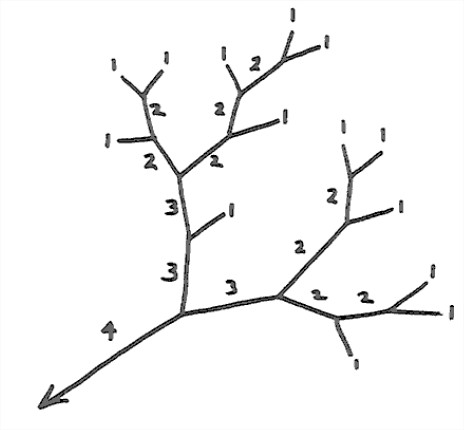
The convention is that the fingertip channels (those with no tributaries) are called first-order streams. The junction of two first-order streams produces a second-order stream, and the junction of two second-order streams produces a third-order stream, and so on. Another convention is that the junction of a stream of given order with a stream of lower order doesn’t change the order of a higher- order stream. The trunk stream of the drainage basin—the one by which the given drainage basin is actually defined, by choosing a given point on that stream—is the highest-order stream associated with that drainage basin.
The various relationships between stream order and length, area, and number properties of drainage basins have come to be known as Horton’s laws. Horton's law of stream orders states that
The numbers of streams of different orders in a given drainage basin tend closely to approximate an inverse geometric series in which the first term is unity and the ratio is the bifurcation ratio.
(The bifurcation ratio is the ratio of the number of streams of a given order to the number of streams of the next highest order.) By the nature of a geometric series, this means that when you plot the logarithm of the number of streams of a given order against the stream order you tend to get a straight line (Figure 3-46). Graphs of this kind are called Horton diagrams. Most of the curves in Horton diagrams tend actually to be slightly concave upward rather than being a straight line. Analysis of all the studies that have been published shows that this is a strong tendency. There are similar laws for other characteristics of the drainage network: the length of stream segments between confluences, and the drainage areas of stream segments.
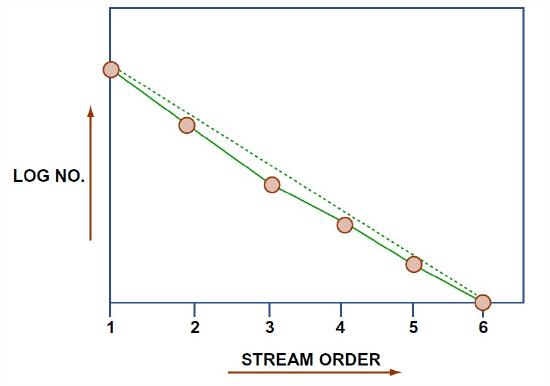
An important observation is that Horton’s law holds for almost all watersheds that have been studied, in all kinds of areas, with all kinds of climates and bedrock types. Although there seem to be some deviations caused by lack of isotropy and homogeneity of the bedrock structure and composition, the law of stream numbers on the whole is quite insensitive to such geologic controls. This suggests that there must be some very general basic cause.
Another interesting observation is that the bifurcation ratio also seems to be insensitive to geologic controls as well as to climate. It can be shown theoretically that the bifurcation ratio can never be less than 2; it’s always between 3 and 5, and usually around 4. It shows only a small range of variation from region to region and from environment to environment, except where powerful geologic controls dominate.
Much effort has been expended to try to interpret the meaning of Horton’s law of stream orders. Although there are dissenters, it’s widely accepted that Horton’s law is a manifestation of randomness in the topological development of the drainage network. In a classic paper, Shreve (1966) showed that the assumption that all topologically distinct possibilities for how streams of a given order combine to form a network are equally likely leads to the characteristically slightly concave-up curves on Horton diagrams.


