5.9: Morphology and Dynamics of Meandering Streams
- Page ID
- 14309
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The two most characteristic plan patterns assumed by rivers are meandering and braided. First of all, keep in mind that the tendencies toward meandering and braiding are complementary rather than mutually exclusive, in the sense that many rivers show elements of both at the same time and within the same reach.
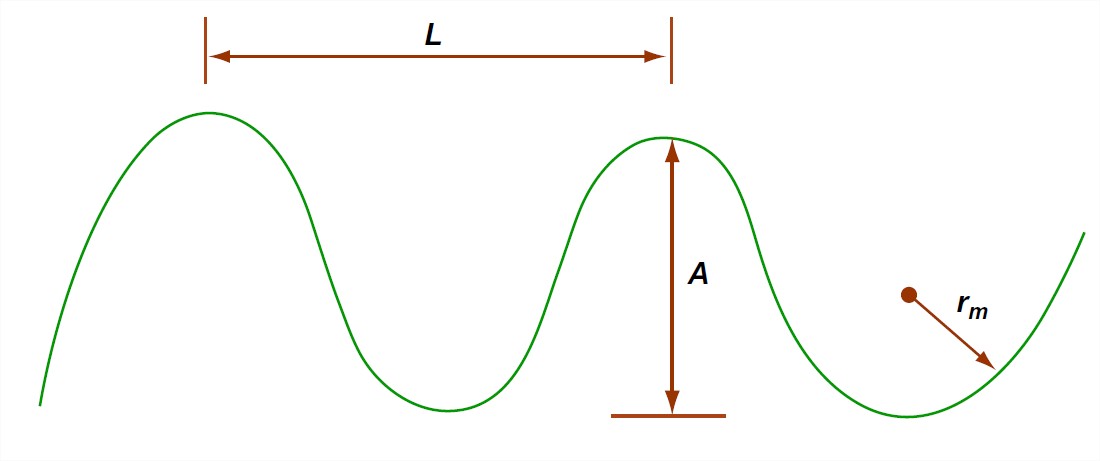
First, some descriptive stuff on the geometry of meandering rivers. Figure 5-36 shows most of the elements of a meandering river system. The meander bends or meander loops are never perfectly regular, but they are often described as if they were (Figure 5-37), in terms of wavelength and amplitude. One can also think about a radius of curvature in the bend, but that’s likely to vary from point to point in the bend. The narrow part of the meander bend, between adjacent reaches of the channel above and below the bend, is called the meander neck.
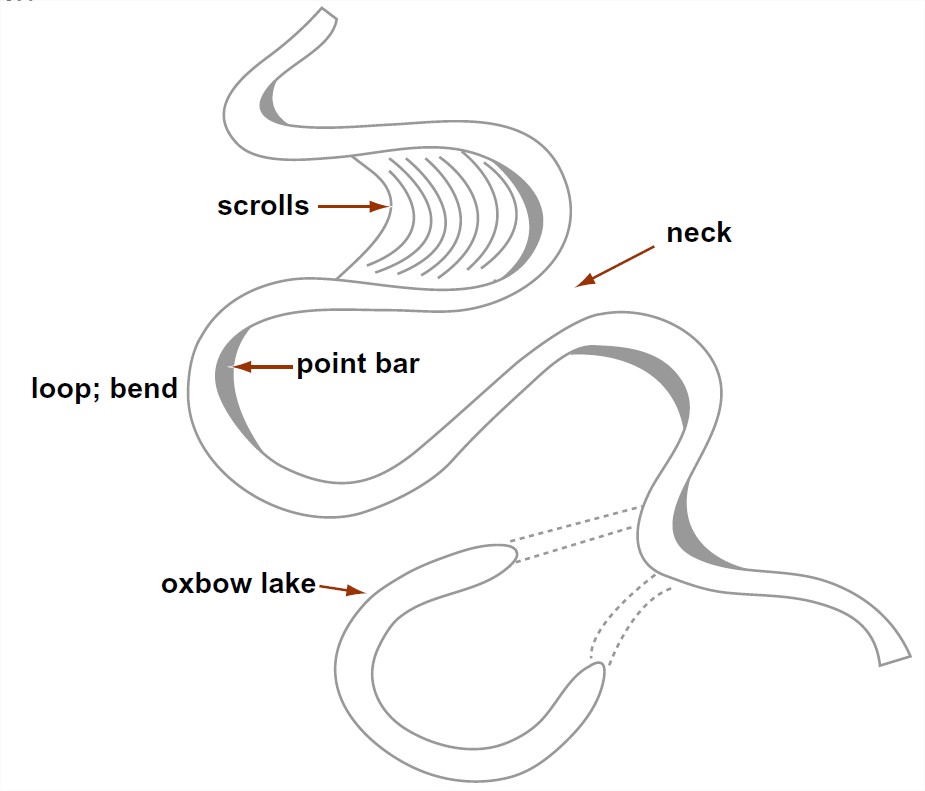
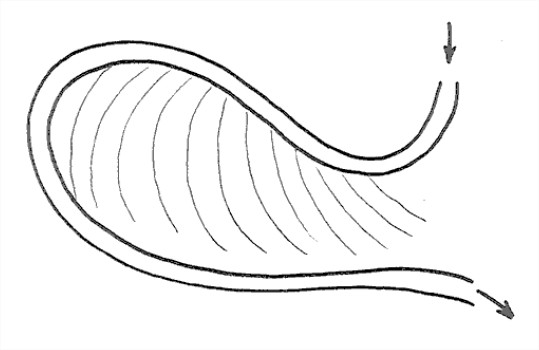
On the inner, or convex, side of the meander bend is a fairly smooth and largely non-vegetated body of sand, sloping gently downward toward the center of the channel. This sand body, called a point bar, lies everywhere below bank-full stage and is inundated by floods. Sediment is gradually accreted to the point-bar surface, causing the point bar to shift laterally. Point-bar deposits are for
On the outer, or concave, side of the meander bend is a steep bank or cliff, often called a cut bank, of consolidated or semiconsolidated sediment that is eroded during strong flows. The bank is eroded by various processes, the most important of which is undercutting low on the bank and collapse of large masses into the channel.
The flow-transverse profile of a meandering river is highly asymmetrical. The flow is deepest near the foot of the eroding outer bank, and it shoals gradually up the point-bar surface. The velocity of flow is highest in the region near the free surface and near the outer bank. Figure 5-38 is a cartoon of the flow-transverse profile, showing the characteristic pattern of isovels (lines of equal velocity). There’s also a characteristic helical secondary circulation within the bend, such that the flow near the bed has a component inward toward the point bar, and the flow near the surface has a component outward toward the outer bank. This spiraling secondary circulation is readily explained by the differences in centrifugal force between the high-speed regions of the flow above and the low- speed regions of flow below. It’s this secondary circulation that causes the accretion on the point-bar surface.
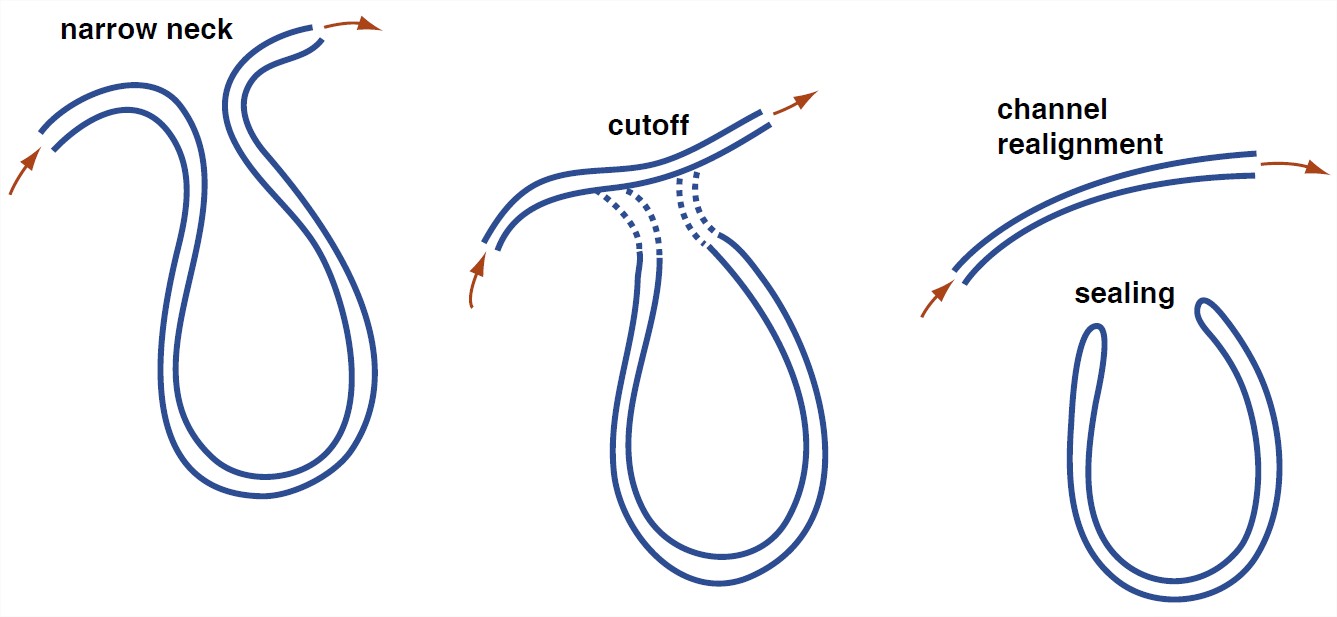
Meander bends generally have a tendency to change with time toward larger amplitudes and narrower necks. Eventually, the river jumps across the narrow neck during a flood. Such an event is called meander cutoff, or neck cutoff. The river thereby straightens itself spectacularly in quantum jumps to offset the gradual amplification of the meander bends. Sometimes there’s a less catastrophic variety of meander cutoff, whereby the river occupies an old slough that marks an earlier position of the bend; then the amplitude decreases, but not nearly to zero. Cutoffs of that kind are called chute cutoffs (because the river comes to occupy a chute between the two sides of the bend).

Point bars tend to be built episodically, during floods. The earlier positions of the top of the point bar are marked on the floodplain on the inner side of the meander bend by low and curving ridges arranged congruently within the meander bend (Figure 5-39). These curving ridges are called meander scrolls or meander scars. One of the best kinds of evidence that the bend shifts in position as it grows is the truncation of earlier meander scrolls by the present channel.
The ends of an abandoned meander loop soon become plugged by fine sediment to form an oxbow lake (Figure 5-40). Oxbow lakes are filled in very slowly by deposition of fine sediment during overbank flows on the floodplain. Their outlines in the floodplain remain visible from the air long after they are filled, however, owing to slight differences in color and vegetation on the floodplain surface. The floodplains of meandering rivers show a complex pattern of several generations of truncated meander scars and partly or wholly filled oxbow lakes recording a long history of meandering.
Perhaps the best way to approach the problem of the dynamics of meandering and braiding is to think in terms of the development of a meandering or braided pattern in a stream that is initially straight and regular and flowing within a homogeneous floodplain. This kind of thing is easy to do in a wide flume in the laboratory (Figure 5-41): put the sediment in, homogenize it by hand, level it off, and then carve a regular channel in it. (You could fairly easily build apparatus in which to do this in your own backyard, which by now is getting rather crowded.) When a uniform sediment-moving flow is then started in the channel, the channel remains straight and regular for a long time, but eventually, after hours or even tens of hours, the inevitable little irregularities of the initial channel lead to an alternating pattern of erosion and deposition along the banks and therefore to increase in sinuosity of the channel.
If the banks of the laboratory stream are freely erodible (that is, if they consist of loose sand and gravel, rather than cohesive muds) then the channel pattern is at first regularly sinuous but eventually becomes highly irregular and braided. It’s not nearly as easy to do this experiment in cohesive materials, but what’s been done shows that in cohesive banks the braiding does not develop, but instead a statistically steady process of meander growth and cutoff develops.
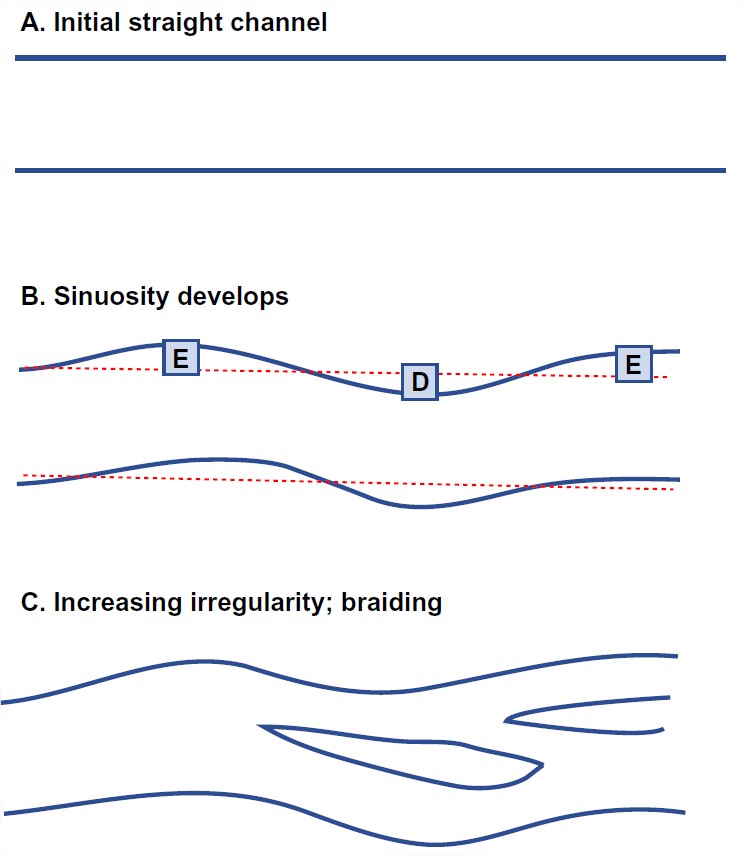
So you can see that a natural approach to the dynamics of meandering is to treat meandering as what the experts call a stability problem. In such an approach one attempts to capture the physics of the process, in terms of the interaction between the flow and the sediment transport, in the form of a set of equations, and then one attempts to linearize those equations in order to apply them to the behavior of a very-small-amplitude perturbation of an originally straight channel. If the perturbation is damped, then the straight channel is stable; if the perturbation is amplified, then the straight channel is unstable. The fastest-growing wavelength of the disturbance is the one that should specify the scale of the resulting meanders. Although the full equations may not be workable for determining the evolution of the meandering pattern once the disturbances have a finite amplitude, various other lines of attack have been brought to bear on particular aspects of finite-amplitude meanders, with considerable success.
On a more concrete note, it’s widely agreed that the most important factor in determining whether a river meanders is bank stability. A floodplain with a large percentage of fine, cohesive sediment in it is conducive to meandering, as is a dense cover of vegetation. If the sediment is noncohesive and freely erodible, and the climate is inconducive to vegetation, the river braids rather than meanders. Incidental note: before the Silurian, when there were no land plants, there is no evidence of meandering streams, only braided streams.


