5.8: Fluvial Sediment Transport
- Page ID
- 14308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This section is a brief account of the nature of sediment transport in rivers.
Regolith is produced by weathering of bedrock on the continents and is then transported away from the site of production as sediment (transported regolith), in both particulate and dissolved form. The oceans can be viewed as the repository for this sediment, although much is stored in sedimentary basins on the continents and recycled into new continental bedrock on time scales that may be a large fraction of geologic time.
Rivers are by far the most important carriers of sediment on the continents, although glaciers have been even more important at certain times and places. So although the essence of rivers is that they are flows of water, one of their most outstanding characteristics is that they are also transporters of sediment. I think it’s fair to say that most of the interesting things about rivers are connected in some way with the sediment-transporting nature of rivers, either directly or indirectly. Fluvial sediment transport is an important area in several different disciplines: fluvial engineering, geomorphology, and sedimentology.
A big problem in gaining an appreciation for sediment transport in rivers is that it’s generally difficult to observe sediment transport in real rivers, unless they are very shallow and not carrying much sediment. A good way to get around this difficulty, in part, is to build an artificial river in your backyard and watch from close up how the river transports its sediment.
It’s not difficult to build a simplified small river that reproduces many of the essential aspects of fluvial sediment transport. Nail together a large wooden channel, open at the top and with a rectangular cross section (Figure 5-30). Caulk the seams and joints so they won’t leak intolerably. (All such channels leak a little sometimes, even in the fanciest of laboratories.) The channel might best be about a meter wide and a few tens of meters long, but I realize that’s a big order for backyard construction; you could get away all right with a channel no more than ten to twenty centimeters wide and five to ten meters long.

At its downstream end the channel should pass into a big open tank. Install a pump and some piping to take the water from the downstream tank and recirculate it to the upstream end of the channel. (This is by far the most expensive and, for most people, the most challenging part.) A valve in the return pipe lets you adjust the water discharge. You might mount the whole channel on a jack near the upstream end, so that you can change the slope of the channel easily, but that isn’t really necessary. It would also be nice to make at least one sidewall of the channel out of glass or transparent plastic, for good viewing of the sediment transport. At the very least, install a few small subsurface portholes in the channel walls. Place a thick layer of sand on the floor of the channel. The mean size of this sand might be as fine as 0.1 mm or as coarse as 1 mm, but to see the widest range of phenomena and features use a sand with a mean size a little less than 0.5 mm.
Threshold of Movement
Now you are ready to make some experiments (flumologists— scientists and engineers who work with channels of the kind you just built in your back yard, which are called flumes— call them runs) in your channel. For each run, fill the tank and the channel with water to establish the depth of flow, turn on the pump, and adjust the valve for a certain water discharge and therefore (given the flow depth) a certain mean flow velocity. Arrange each run to have a flow depth as great as the flume will allow, ideally at least a large fraction of a meter.
The first thing you should do is study the beginning of sediment movement. (First, it would be good to smooth off the sand bed to be planar. That’s not hard to do if you use an underwater scraper blade attached to a device that slides along the top edges of the channel walls.) Clearly, if the flow is too slow it won’t move any sediment. As you gradually increase the flow velocity, however, at some point some sediment particles begin to move. That point is called the threshold of movement. It may surprise you to find how difficult it is to define or locate the threshold, because there’s weak movement or slight movement over a wide range of flow strengths. The problem of the threshold of movement reflects two questions that have long been recognized as important in fluvial sediment transport:
- How strong a flow is needed to initiate the transport of a given sediment?
- How coarse a sediment can be moved by a given flow?
The second question has to do with what’s called the competence of a river. Just to give you some feel for the flow strength needed to move the sand in your channel, you would have to produce a current velocity of about 0.2 m/s to reach threshold conditions—depending on the sand size, of course, and on the water depth also.
Now make some runs with flow velocities greater than the threshold value, to study the modes of particle movement. The aggregate of sediment particles which are transported by a flow at a given time is called the sediment load, or just the load. The load can further be subdivided in three different ways: on the basis of
- its physical nature;
- its presence or absence in the bed; and
- how it travels.
On the basis of its physical nature, the sediment load of rivers is conventionally subdivided into particulate load and dissolved load. Does it surprise you that in general the dissolved load is of the same order of magnitude as the particulate load? Keep in mind that the concentration of the dissolved load doesn’t depend greatly on the discharge, so there’s a lot of dissolved load even at times of low discharge. In fact, there tends to be an inverse correlation between discharge and dissolved load, for the understandable reason that at times of high discharge most of the water in the river has run off the surface without spending a long time in contact with regolith and bedrock, where, by the variety of weathering processes you learned about in Chapter 2, the solutes of the dissolved load come from.
The load can also be divided into bed-material load, which is that part of the load whose sizes are represented in the bed in non-negligible percentages, and wash load, which is that part of the load whose sizes are not present in the bed in appreciable percentages. The wash load, which is always the finest fraction of the load (mainly clay or finest silt size), is carried through a long segment of a river without any exchange of sediment between the bed and the flow. Of course, you don’t have any wash load in your backyard channel, unless you choose to dump in some water containing a suspension of fine clay.
In real rivers, much of the very finest fraction of the load has such a small settling velocity that it travels for long distances before settling to the bed, and even when it reaches the bed it tends to be resuspended immediately. So the finest fractions of the sediment are represented almost not at all in the bed material in the river channel. Only in overbank areas during floods, where the water velocities are small, is the wash load deposited. Even there, storage tends to be temporary, because shifting of the river channel tends eventually to re-erode the fine sediment that was previously deposited on the floodplain.
Finally, the load can be divided into bed load, which travels in direct contact with the bed or so close to the bed as not to be substantially affected by the fluid turbulence, and suspended load, which is maintained in temporary suspension above the bed by the action of upward-moving turbulent eddies (Figure 3-31). I hope it’s clear from these definitions that bed load is always bed-material load, and suspended load is likely to be partly bed-material load and partly wash load, although in particular cases it could be all wash load, or all bed-material load.
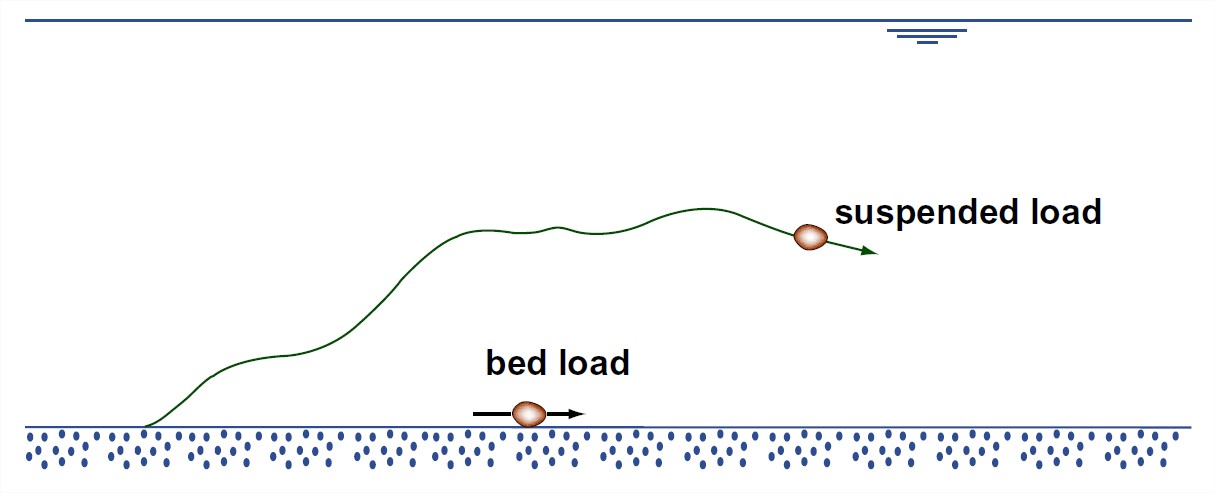
This may sound confusing, but it makes sense. Figure 5-32 may or may not help.
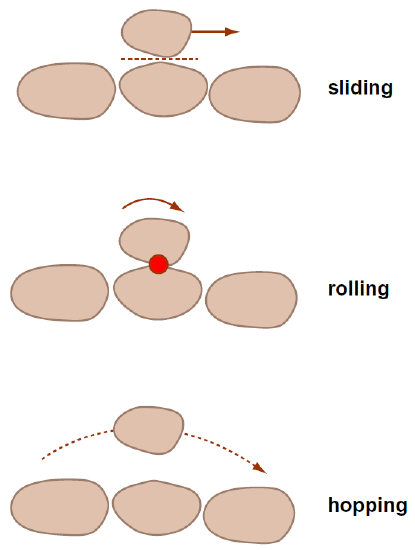
The movement of bed load is sometimes called traction. Bed-load movement can be by rolling, sliding, or hopping (Figure 5-33). It’s not easy to observe bed-load movement in detail, but, if you’re a good photographer and you made a high-speed close-up motion picture of bed load, you see that the particles characteristically take occasional excursions downstream, by rolling or hopping or bulldozing irregularly with brief stops along the way, and then come to rest for some time before being moved again. Once a grain is dislodged from a place of rest, it’s susceptible to continued movement by the flow until it finally finds a rather sheltered position among the bed particles, at favorable sites called “pockets”, and then it’s not dislodged again until it’s affected by an especially near-bottom eddy or until one or more of the bed particles sheltering it are themselves put into motion.
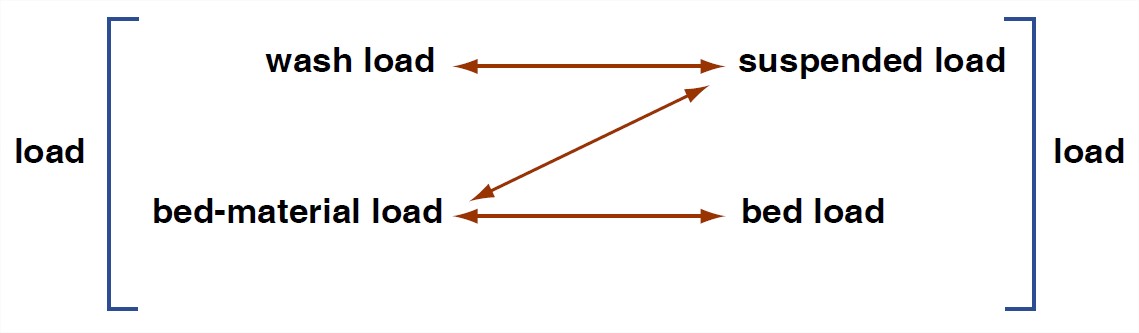
If you’re a keen observer you would notice that the set of particles that form the load keeps changing from time to time, because particles are continually coming to rest and being set into motion again. Also, there’s a problem in distinguishing between bed load and suspended load: how far can a grain move up into the flow and still be considered bed load? The standard criterion is whether or not fluid turbulence has a substantial effect on the time and distance involved in the excursion. Although the distinction between bed load and suspended load is a convenient one, there’s no sharp break between bed load and suspended load. Also, a given particle can be part of the bed load at one moment and part of the suspended load at another moment, depending upon the time history of fluid forces and motions to which it is subjected. (And of course at still other times the same particle might not be moving at all.) Therefore, at any given time there’s an appreciable overlap in the size distributions of the bed load and the suspended load, although clearly the suspended load tends always to be finer on the average than the bed load.
Particles moving as bed load are susceptible to being carried up into suspension when the maximum vertical turbulent velocity fluctuations are greater in magnitude than the settling velocities of the particles. If the conditions of the flow and the settling velocities of the particles fulfill that condition, then some of the moving bed-load particles occasionally find themselves caught in a strong upward-moving eddy, and the particle is carried for some distance above the bed. The particle is affected by a series of eddies as it moves downstream; depending on the motions of the individual eddies, the particle may rise only a short distance from the bed and travel only a short distance downstream before it settles back to the bed, or it may rise high above the bed, even almost to the water surface, and travel far downstream. Obviously, the smaller the settling velocity and the stronger the turbulence, the greater the average height above the bed and the greater the distance of downstream travel by the particle.
The sediment particles are not really suspended above the bed, in the way that a painting is suspended on a nail in the wall: they are always settling back toward the bed and will eventually return to the bed. Only particles of colloidal size, much finer than a micrometer, can be truly suspended. Such particles have such small mass that Brownian motions caused by the random collisions of molecules against the particle keep the particle in permanent suspension.
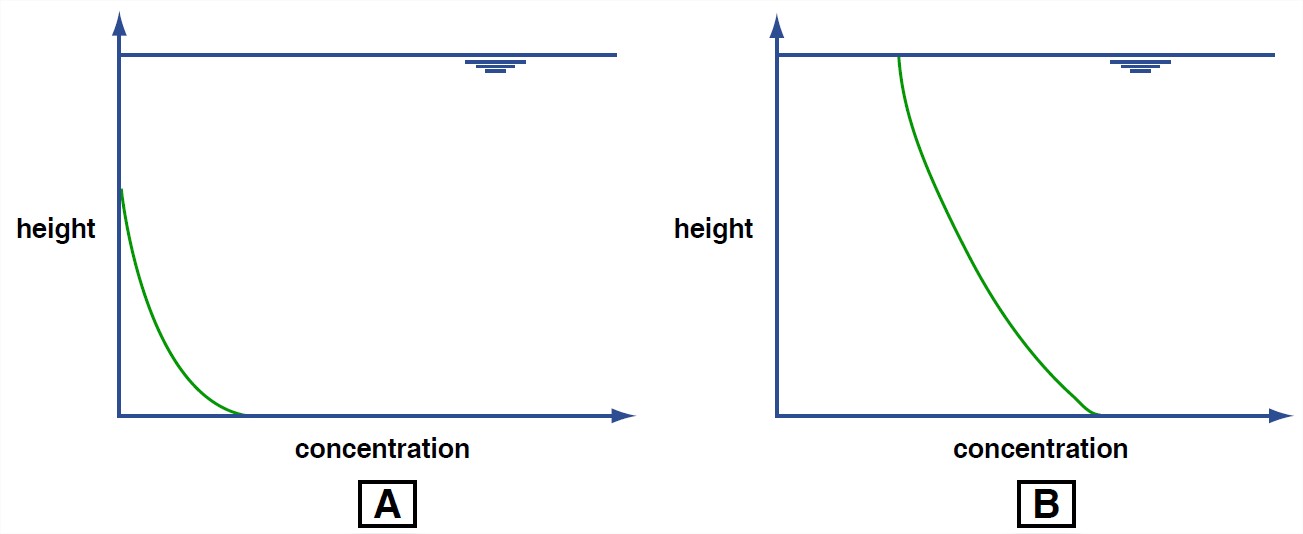
When the flow is relatively weak and/or the sediment is relatively coarse, the concentration of suspended sediment drops off rapidly upward, and the upper part of the flow may not have any suspended sediment at all (Figure 5-34A). When the flow is relatively strong and/or the sediment is relatively fine, however, suspended sediment is present throughout the entire depth of flow, and the concentration of suspended sediment drops off only slightly upward (Figure 3-34B).
Classification of Rivers by Sediment Load
It should seem natural to you that some rivers, especially those whose sediment sources consist mostly of coarse sand and gravel, carry mostly bed load. Such rivers are called, understandably, bed-load rivers. On the other hand, the sediment sources of some rivers are mainly clay, silt, and fine sand. The sediment load of such rivers is mainly suspended load. Such rivers are called suspended- load rivers. Finally, in a great many rivers both bed load and suspended load are important; such rivers are called mixed-load rivers. Keep in mind that this classification is very loose, both because there’s a continuous gradation in nature of sediment load from river to river and also because a given river carries its load in different ways, depending on its discharge at the given time.
You can also classify rivers by the dominant particle size of the bed material, into gravel-bed rivers, sand-bed rivers, and (much less common than the first two) mud-bed rivers. (Of course, there are gradations among these three kinds.) In most sand-bed rivers, most of the bed-material sediment discharge on average is in the form of suspended load. In gravel-bed rivers, on the other hand, most of the sediment discharge is accounted for by bed-load transport.
Sediment Transport Rate
The rate at which sediment is moved past a cross section of the flow is called either the sediment transport rate or the sediment discharge. It’s related to the sediment load, but it’s different, just because different fractions of the sediment load are transported at different rates. It can be measured in mass per unit time, or in weight per unit time, or in volume per unit time. For many decades hydraulic engineers have sought after formulas to predict the sediment discharge that’s associated with some combination of flow conditions and sediment characteristics in some reach of a river. There are many such formulas, but none of them work gratifyingly well.
To derive a sediment discharge formula, you try to think about the physics of sediment transport in a way that allows you to develop the form of some rational equation for transport rates, which contains within it one or more “adjustable parameters” whose values are assigned by analysis of selected data sets already at hand. It’s a sad fact that the physics of sediment transport is so complicated that you can’t develop an equation from the first principles of physics that contains no such adjustable parameters. It’s almost no exaggeration to say that there are dozens of sediment discharge formulas in the hydraulic-engineering literature. The physical basis behind these formulas ranges widely, and none of them does a really good job.
Here’s just the barest start at deriving a sediment discharge formula. Your common sense tells you that the stronger the flow the greater the sediment transport rate. And an important first-order fact of observation is that the sediment transport rate is a very steeply increasing function of the flow strength. Think about the simplest way to embody these important facts in a formula for the sediment transport rate per unit width of flow, usually written \(q_s\). Perhaps the simplest approach to quantifying \(q_s\) is to write an expression like
\[q_{S}=A \tau_{\mathrm{o}}^{n} \label{8.6}\]
where \(A\) is a coefficient and \(n\) is an exponent much larger than one. Better yet, \(\tau_o\) might be replaced with \(\tau_o\)-\(\tau_c\), where \(\tau_c\) is the threshold boundary shear stress for sediment movement. The trouble with Equation \ref{8.6} is that it has no strong basis in the actual physics of the transport. The true situation must be much more complicated than Equation \ref{8.6}. But with \(A\) and \(n\) adjusted by use of observational data, Equation \ref{8.6} can serve for very crude estimates of \(q_s\).
Measuring the sediment transport rate is a notoriously difficult task. The suspended-load transport rate is usually measured by trapping small samples of the passing flow, with its suspended sediment, in a series of little catch bottles arranged vertically through the entire depth of the river, together with measurements of the local flow velocity along that vertical. Bed load is more difficult to measure. Usually bed load is measured with devices called bed-load traps or bed-load samplers. Think in terms of those pole-mounted dustpans that are used to sweep litter from paved surfaces—but with netting in the back of the pan to let the water flow through. They come in all sizes and geometries, but their purpose is to catch all the bed load that comes upon the trap from upstream— without catching too much or too little. Unfortunately there are many practical problems connected with bed-load traps.
Bed Configuration
Now you need to make a series of runs in your channel to study the bed configuration. By the term bed configuration I mean the overall bed geometry that exists on the bed of the channel at a given time in response to the flow. If you haven’t had any experience with bed configurations, you may be thinking, “What’s the big deal? Won’t the sediment just move on a planar transport surface?” But it turns out that you would just as often be wrong about that than right. If the bed configuration is not planar, it’s composed of individual topographic elements called bed forms.
Make a series of runs with slightly increasing mean flow velocity above threshold conditions. In each run, let the flow interact with the bed long enough for the bed configuration to be statistically steady or unchanging. After that time the details of the bed configuration change constantly but the average characteristics remain the same. The time required for the flow and the bed to come into a new state of equilibrium might be as little as a few minutes to as long as several days, depending on the sediment transport rate, the size of the bed forms that develop, and the extent of modification of bed forms that were left over from the preceding run.
At low flow velocities, the bed becomes covered with ripples: little ridges of sand with their crests and troughs oriented mostly transverse to flow but rather irregular in detail, with gentle upstream surfaces and generally angle-of- repose downstream surfaces (Figure 5-35A). Their spacings are 10–20 cm, and their heights are a few centimeters. They move slowly downstream, orders of magnitude slower than the flow velocity, by erosion of sand from their upstream sides and deposition on their downstream sides. Except at the highest speeds, you have to watch them closely to see them move. Ripples on real river beds look almost exactly like those you can produce in your backyard channel.

At a flow velocity that’s a moderate fraction of a meter per second, ripples are replaced by larger bed forms called dunes (Figure 5-35B). Dunes are fairly similar to ripples in geometry and movement, but they are at least an order of magnitude larger. The transition from ripples to dunes is complete over a narrow range of only a few centimeters per second in flow velocity. Dunes in large rivers can attain truly gigantic proportions: heights of over ten meters, and spacings of many hundreds of meters. Superimposed on such large dunes are one or more orders of smaller dunes, all the way down to little ripples.
As you increase the flow velocity further the dunes become lower and more rounded, over a fairly wide interval of flow velocity, until finally they disappear entirely, giving way to a planar bed surface over which abundant suspended load as well as bed load is transported (Figure 5-35C). Judging from the appearance of the bed after the flow is abruptly brought to a stop, the transport surface is strikingly planar: relief is no greater than a few grain diameters. But it’s difficult to observe the mode of grain transport over the planar bed because the bed is obscured by abundant bed load and suspended load.
As you increase the flow velocity still further, subdued standing waves appear on the water surface, and the resulting pattern of higher and lower near-bed flow velocity causes the bed to be molded correspondingly into a train of waves that are in phase with the water-surface waves. Under certain conditions these coupled bed waves and surface waves increase in height and become unstable: they move slowly upstream and at the same time grow in height, until they become so steep that they break abruptly, throwing much sediment into suspension (Figure 5-35D). The bed and water surface then revert to a planar or nearly planar condition, whereupon the waves build again and the cycle is repeated. Because of their upstream movement these forms are called antidunes. Antidunes are important in shallow fast-flowing rivers but not in deep rivers. An excellent place to watch small antidunes in action is at the beach where a small stream, flowing fast and shallow, passes across the sandy beach to reach the sea.
More on Fluvial Hydraulics
Back in Section 4 I put off discussion of the following important question: What determines the particular combination of flow depth and flow velocity associated with a given water discharge? I can pick that up again, now that I’ve said some things about bed configurations.
The force the flow exerts on the bed of a river are of two kinds: skin friction and form drag:
- Skin friction (a term borrowed from aerodynamics of airplane wings) is the local friction force exerted on locally smooth areas of the river bed.
- Form drag is the force the flow exerts on a non-planar part of the river bed, like a ripple or a dune, by exerting higher fluid pressure on the upstream side of the form than on the downstream side.
Just think back to the swimming-pool experiment with the tray or pizza pan, described in Chapter 1. In almost all river flows, the form drag is much larger than the skin friction.
It’s easy to understand that the particular combination of depth and velocity for a given discharge in a river is mediated by the nature of the flow resistance: the greater the flow resistance, other things being equal, the deeper and slower the flow. And, as you can easily imagine given the ruggedness of ripples and dunes on a river bed, the flow resistance is dominated by form drag whenever there are bed forms on the river bed. So the most important factor in determining the combination of depth and velocity is the nature of the bed configuration.
This bed-configuration effect on the flow resistance has an important and beneficial consequence for the behavior of rivers during floods. As the discharge and therefore the flow velocity increases during a flood, the bed configuration is ripples and then rugged dunes, so the flow depth is relatively deep and the flow velocity is relatively low. As the velocity increases, however, eventually the dunes are washed out to a plane bed, and as the discharge continues to increase, the flow depth is then relatively low and the velocity is relatively high. (The word relatively in the last two sentences implies comparison with the same discharge but a different bed configuration.) The highest stage during the flood, when the bed is planar, is typically even greater than what it was at the time of transition from dunes to plane bed, but the important thing is that the stage is much less than it would have been if this bed-configuration effect did not exist—as in a bedrock river, for example.
The Sediment Yield
I need to introduce just one more thing about sediment in rivers. You should make a distinction between the sediment discharge and what’s called the sediment yield of a river. The sediment yield is the sediment discharge divided by the total drainage area of the river upstream of the cross section at which the sediment discharge is measured or estimated. The sediment yield measures the rate, per unit area, at which sediment is removed from the watershed. It’s important in studies of the long-term evolution of landscapes drained by rivers.


