5.3: Open-Channel Hydraulics
- Page ID
- 13476
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This would a good place to go back and review the material on open-channel flows in Chapter 1. Recall that in open-channel flows the presence of the free surface means that the geometry of the flow can change in the flow direction not just by being constrained to do so by the geometry of the boundaries but also by the behavior of the flow itself. This means that the acceleration of gravity can no longer be ignored, because the forces of gravity help shape the free surface. For example, gravity waves can be generated on the free surface. But the effect of gravity is more far-reaching than just that. Babbling brooks and white-water rivers clearly have complex free-surface geometries governed by bed relief, expansions and contractions of the channel, and, less obviously, upstream and downstream conditions. But all open-channel flows, even broad, majestic rivers like the Mississippi, are subject to such effects of gravity.
Here are three basic concepts in the hydraulics of open-channel flow I think you should know about:
bed shear stress: The bed shear stress is the force per unit area the flow exerts on the bed. Actually the force per unit area varies strongly from point to point, depending on the details of the bed geometry, and the concept of boundary shear stress is built around the idea that you average over an area large enough to eliminate the effects of such things as sediment particles or local sediment topography. The importance of the bed shear stress lies in its role in moving the sediment particles resting on the river bed.
flow resistance: The resistance to flow, or flow resistance, is the force or drag the boundary exerts on the flow. You should recognize that in uniform flow, where the flow isn’t accelerating or decelerating, Newton’s third law tells us that this is just the opposite of the bed shear stress. The importance of the flow resistance is less easy to state. It has to do with the role of flow resistance in determining the particular combination of flow depth and flow velocity (out of an infinite number of possible combinations) with which the imposed water discharge is passed through a given reach of a river (Figure 5-11).
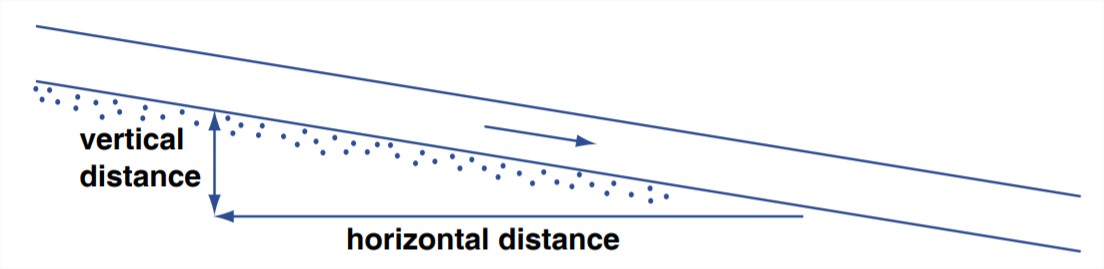
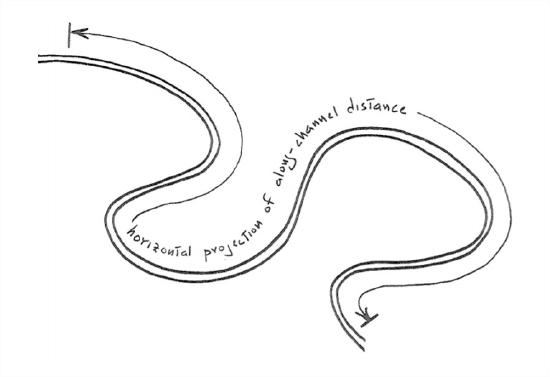
slope: If rivers were always straight, the definition of the slope would be a straightforward concept: it’s the difference in water-surface elevation between two stations along the river, divided by the horizontal distance be stations (Figure 5-12). But if the river is curvy (as is usually the case, at least to some extent), then you have to measure the horizontal distance along the sinuous projection of the course of the river on a horizontal plane (Figure 5-13). The slope can be measured in feet per mile (as in the U.S.) or in some metric units like meters per kilometer. Recalling some trigonometry, you might recognize the slope as the tangent of a slope angle. Measuring the slope of a river is not easy: you have to do some surveying to establish elevations, and you have to worry about what, exactly, is the course of the river.
Advanced Topic: The Resistance Equation For Open-channel Flow
1. It’s easy to derive a fundamental equation that relates the flow depth, the slope, and the bed shear stress of a river, if you are willing to assume that the flow in the river is about the same in cross-sectional shape and area at all cross sections (such rivers are said to have uniform flow, which is often close to being the case).
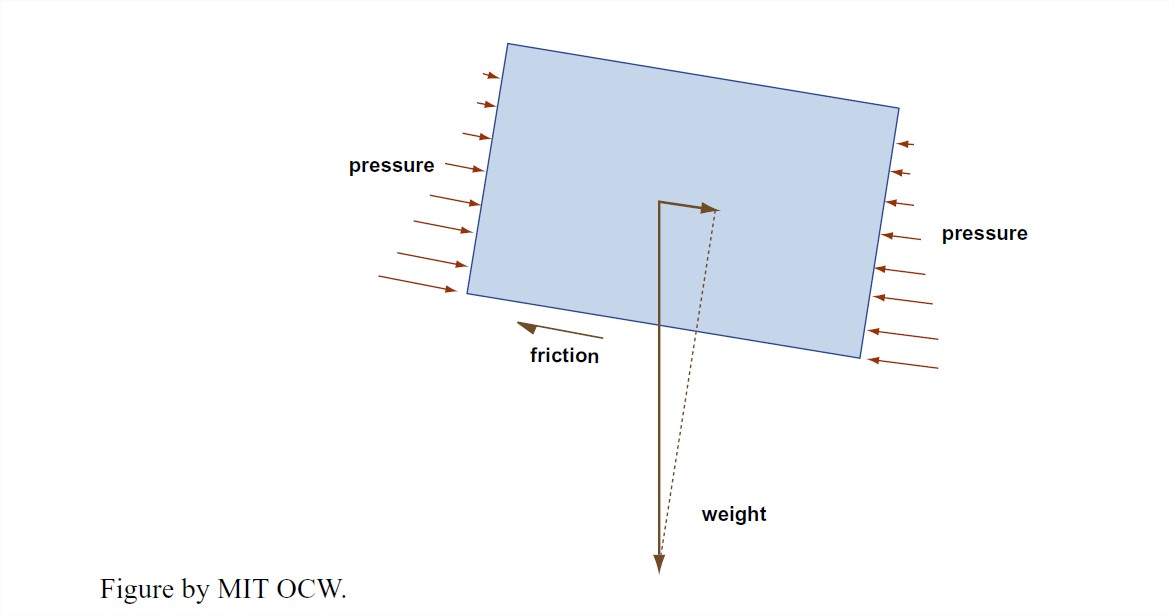
2. Think about the water contained in a volume that’s formed by the river bed, the free surface, and two cross sections a unit distance apart (Figure 5-18). One of the classic ways to get somewhere in the analysis of a problem in dynamics (and we’re dealing with such a problem here) is to apply Newton’s second law, F = ma, where F is the force on some body of matter, m is the mass of the body, and a is the acceleration of that body under the action of that force) to an appropriately chosen part of the dynamical system. What I want you to think about here are the forces that act on the water in the volume I just defined, which from now on I’ll refer to as the “body”. Because the flow is uniform, and the river discharge varies only slowly with time, it’s a good assumption that the body is not accelerating. So Newton’s second law tells us that the sum of all the forces acting on the body in the streamwise direction has to be zero.
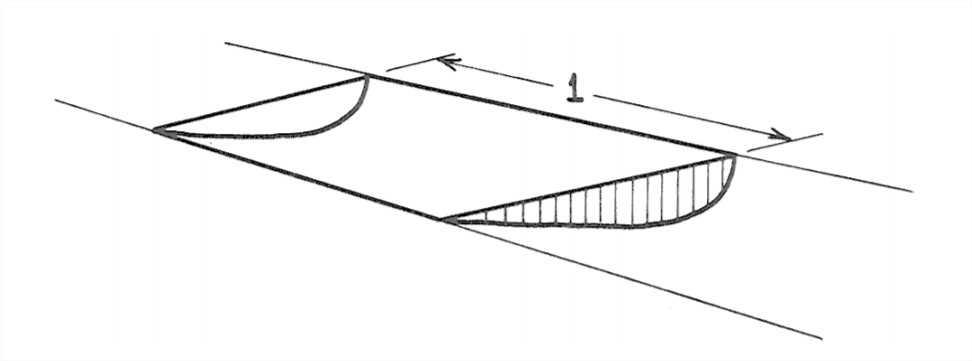
3. What are the forces acting on the body in the streamwise direction (Figure 5-15)? First of all there are hydrostatic fluid pressure forces on both the upstream and downstream faces of the body. We can forget about these, because they are the same upstream and downstream and they act opposite to each other. There’s the weight of the body—that’s a gravity force acting vertically downward—and a component of that weight acts in the downstream direction. It’s this downstream component of the weight that pulls the water down the channel. If the weight per unit volume of the water is γ , and the cross-sectional area of the flow is A, and the slope angle is α, then the downstream component of the weight is (1)(A)(γ )sinα. Finally there’s the upstream-directed frictional force exerted by the boundary on the moving body. It’s this upstream-directed frictional force that resists the downstream-directed gravity force. If the wetted perimeter of the flow (that is, the total distance along the line of contact between the flow and the bed, as viewed in a cross section normal to the river flow) is P, then the frictional force is (1)(P)(τo). Writing the balance between the frictional force and the gravity force, we have
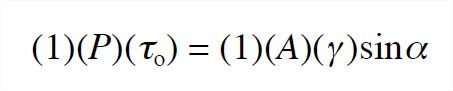
or, doing a little rearranging,
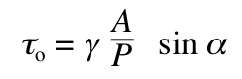
4. A slightly different and more specific way of obtaining a relationship like this is to assume that the width of the river is much greater than its depth, which is often the case. Then, if you look at a body that’s like the one used above but is rectangular volume a unit length long and a unit length wide (Figure 5-16), the downslope component of the weight of the body is (1)(1)(d)sin ��, where d is the flow depth, and the frictional force on the body is (1)(1)( ��o), and the balance equation analogous to Equation 8.3 is
\[\tau_{\mathrm{o}}=\gamma d \sin \alpha\]
These two relationships, Equation 8.3 or Equation 8.4, are called the resistance equation for open-channel flow. A simple result, no? Not many fundamentally important relationships in fluid dynamics are so easy to derive. One useful practical application of the resistance equation is that it gives you a way of finding the bed shear stress once you know the flow depth and the slope—and that’s difficult to do, otherwise.

Now I want to address two questions that get to the heart of how rivers actually operate. Neither of these questions is easy to deal with. The first is this: What determines the slope of a river? One way of answering this question is that the slope is determined by (1) the vertical and horizontal scales of broad crustal uplift that establish the topography that underlies the river system in the first place and (2) the subsequent general reduction in land elevation as the river wears down its drainage area. That’s true, but there’s more to the story, because rivers can meander within their valleys (as you will see in more detail later in this chapter) and thereby increase the length of their course without changing the elevation along their course. A meandering river has a considerably gentler slope than a straight river in the same river valley.
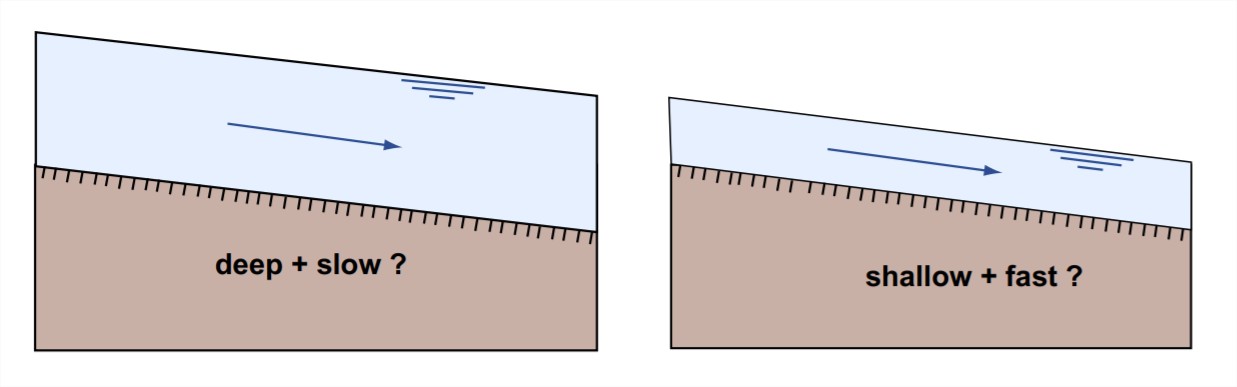
The other question is: What determines the particular combination of flow depth and flow velocity associated with a given water discharge? For any given discharge, there are an infinite number of such combinations; the river might flow fast and shallow, or slow and deep, and still transport the water discharge imposed from upstream. It’s natural to pose this question at this point, but I think it’s wise to postpone an attempt at an answer until we’ve dealt with bed configurations later in this chapter. See Section 8.7.


